
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Контрольная работа №3
|
|
161 - 170. Найти производные 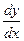 данных функций.
данных функций.
| 161. | 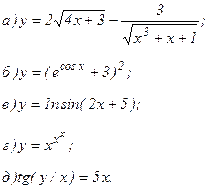
| 162. | 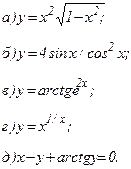
|
| 163. | 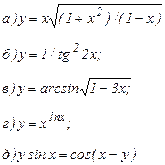
| 164. | 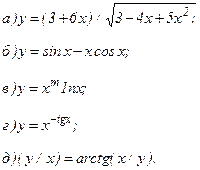
|
| 165. | 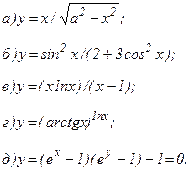
| 166. | 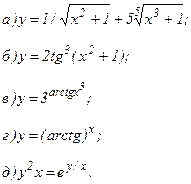
|
| 167. | 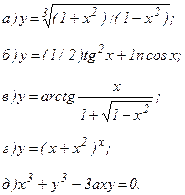
| 168. | 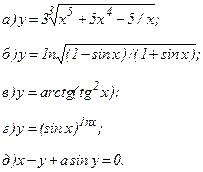
|
| 169. | 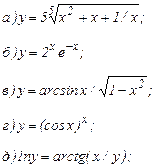
| 170. | 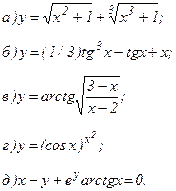
|
171 - 180. Найти 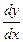 и
и 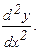
171. 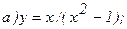
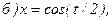
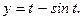
172. 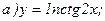
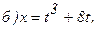
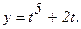
173. 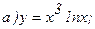
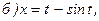
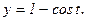
174. 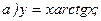
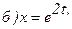
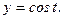
175. 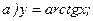
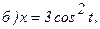
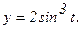
176. 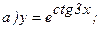
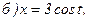
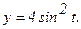
177. 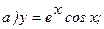
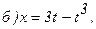
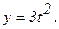
178. 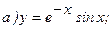
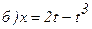 ,
, 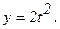
179. 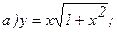
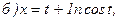
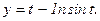
180..
181 - 190. Найти наибольшее и наименьшее значения функции у = f(x) на отрезке 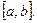
181. 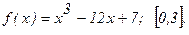
182. 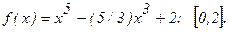
183. 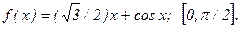
184. 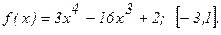
185. 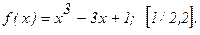
186. 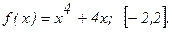
187. 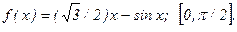
188. 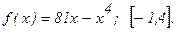
189. 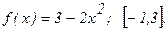
190. 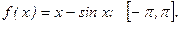
191 - 210. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191. у = 4х/(4+х2) 192. y = (x2-1)/(x2 +1)
193. y = (x2+1)/(x2-1) 194. y = x2/(x-1)
195. y = x3/(x2+1) 196. y = (4x3+5)/x
197. y = (x2-5)/(x-3) 198. y = x4/(x3-1)
199. y = 4x3/(x3-1) 200. y = (2-4x2)/(1-4x2)
201. y = (1nx)/ 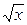 202. y = x
202. y = x 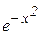
203. y = 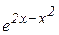 204. y = x2-21nx
204. y = x2-21nx
205. y = 1n (x2-4) 206. y = e1/(2-x)
207. y = 1n (x2+1) 208. y = (2+x2) 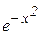
209. y = 1n (9-x2) 210. y = (x-1)e3x+1.
211. Дана функция z = y/(x2- y2)5. Показать, что 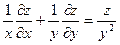
212. Дана функция z = y2/(3x)+arcsin(xy). Показать, что 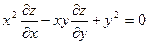
213. Дана функция z = 1n(x2+y2+2x+1). Показать, что 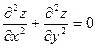
214. Дана функция z = exy. Показать, что 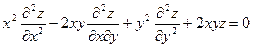
215. Дана функция z = 1n(x+e-y). Показать, что 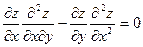
216. Дана функция z = x/y. Показать, что 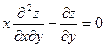
217. Дана функция z = xy. Показать, что 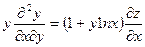
218. Дана функция z = xey/x. Показать, что 
219. Дана функция z = sin(x+ay). Показать, что 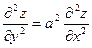
220. Дана функция z = cosy+(y - x)siny. Показать, что 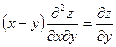
221 - 230. Дана функция z = f(x,y) и две точки А (х0, у0) и В (х1, у1). Требуется: вычислить значение z1 функции в точке В; 2) вычислить приближенное значение 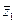 функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С (х0, у0, z0).
функции в точке В, исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке С (х0, у0, z0).
221. z = x2+xy+y2; А (1;2), В (1,02;96)
222. z = 3x2-xy+x+y; А (1;3), В (1,06;2,92)
223. z = x2+3xy-6y; А (4;1), В (3,96;1,03)
224. z = x2-y2+6x+3y; А (2;3), В (2,02;2,97)
225. z = x2+2xy+3y2; А (2;1), В (1,96;1,04)
226. z = x2+y2+2x+y-1; А (2;4), В (1,98;3,91)
227. z = 3x2+2y2-xy; А (-1;3), В (-0,98;2,97)
228. z = x2-y2+5x+4y; А (3;3), В (3,02;2,98)
229. z = 2xy+3y2-5x; А (3;4), В (3,04;3,95)
230. z = xy+2y2-2x; А (1;2), В (0,97;2,03).
231 - 240. Найти наименьшее и наибольшее значения функции z = f(x,y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
231. z = x2+y2-9xy+27; 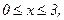
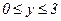 .
.
232. z = x2+2y2+1; 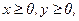
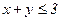 .
.
233. z = 3-2x2-xy-y2; 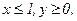
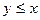 .
.
234. z = x2+3y2+x-y; 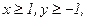
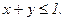
235. z = x2+2xy+2y2; 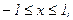
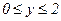 .
.
236. z = 5x2-3xy+y2+4; 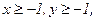
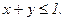
237. z = 10+2xy-x2; 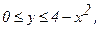
238. z = x2+2xy-y2+4x; 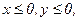
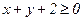 .
.
239. z = x2+xy-2; 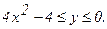
240. z = x2+xy; 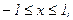
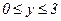 .
.
241 - 250. Даны функции z = z(x,y), точка А (х0,у0) и вектор а. Найти; 1) grad z в точке А; 2)производную в точке А по направлению вектора а.
241. z = x2+xy+y2; А (1;1), а = 2 i - j.
242. z = 2x2+3xy+y2; А (2;1), a = 3i-4 j.
243. z = 1n(5x2+3y2); А (1;1), a = 3i+2 j.
244. z = 1n(5x2+4y2); А (1;1), a = 2 i - j.
245. z = 5x2+6xy; А (2;1), a = i +2 j.
246. z = arctg(xy2); А (2;3), a = 4 i -3 j.
247. z = arcsin (x2/y); А (1;2), a = 5 i -12 j.
248. z = 1n(3x2+4y2); А (1;3), a = 2 i - j.
249. z = 3x4+2x2y3; А (-1;2), a = 4 i -3 j.
250. z = 3x2y2+5y2x; А (1;1), a = 2 i + j.
251 - 260. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b.
251.
| х | |||||
| у | 4,3 | 5,3 | 3,8 | 1,8 | 2,3 |
252.
| х | |||||
| у | 4,5 | 5,5 | 4,0 | 2,0 | 2,5 |
253.
| х | |||||
| у | 4,7 | 5,7 | 4,2 | 2,2 | 2,7 |
254.
| х | |||||
| у | 4,9 | 5,9 | 4,4 | 2,4 | 2,9 |
255.
| х | |||||
| у | 5,1 | 6,1 | 4,6 | 2,6 | 3,1 |
256.
| х | |||||
| у | 3,9 | 4,9 | 3,4 | 1,4 | 1,9 |
257.
| х | |||||
| у | 5,2 | 6,2 | 4,7 | 2,7 | 3,2 |
258.
| х | |||||
| у | 5,5 | 6,5 | 5,0 | 3,0 | 3,5 |
259.
| х | |||||
| у | 5,7 | 6,7 | 5,2 | 3,2 | 3,7 |
260.
| х | |||||
| у | 5,9 | 6,9 | 5,4 | 3,4 | 3,9 |
Date: 2015-04-23; view: 1086; Нарушение авторских прав