Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Контрольная работа №4
|
|
261 - 270. Найти неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.
261. 
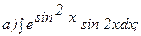
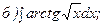
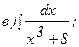
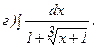
262. 
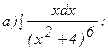
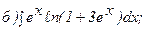
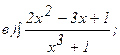
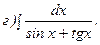
263. 
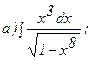
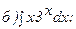
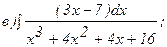
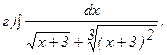
264. 
;
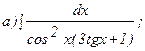
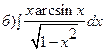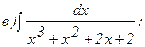
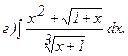
265. 
;
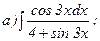
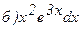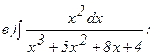
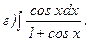
266. 
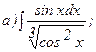
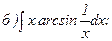
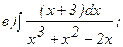
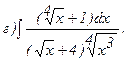
267. 
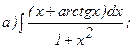
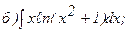
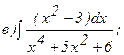
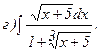
268. 
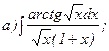
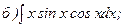
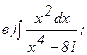
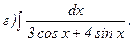
269. 
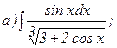
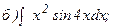
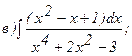
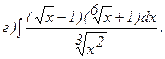
270. 
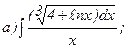
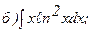
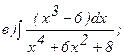
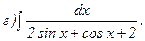
271 - 280. Вычислить приближенное значение определенного интеграла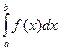 
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
271. 
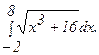
273. 
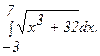
272. 
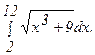
274. 
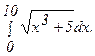
275. 
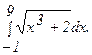
277. 
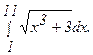
279. 
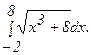
276. 
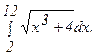
278. 
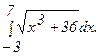
280. 
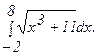
281 - 290. Вычислить несобственный интеграл или доказать его расходимость.
281. 
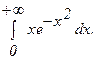
283. 
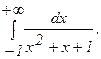
285. 
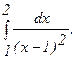
287. 
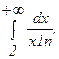
289. 
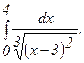
282. 
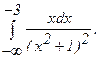
284. 
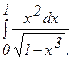
286. 
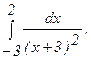
288. 
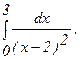
290. 
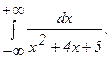
291. Вычислить площадь фигуры, ограниченной параболой у = 3х2 + 1 и прямой у = 3х + 7.
292. Вычислить площадь фигуры, ограниченной одной аркой циклоды х = а(t - sin t), y = a(1 - cos t),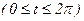 
и осью Ох.
293. Вычислить площадь фигуры, ограниченной кардиоидой r = 3(1 + cos φ).
294. Вычислить площадь фигуры, ограниченной четырехлепестковой розой r = 4sin 2φ.
295. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболами у = х2 и у =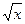 
.
296. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом у =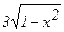 
, параболой х = 
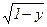и осью Оу.
297. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2/(1 + х2)4 и у = х2.
298. Вычислить длину дуги полукубической параболы у =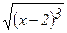 
от точки А (2;0) до точки В (6;8).
299. Вычислить длину кардиоиды r = 3(1 - cosφ).
300. Вычислить длину одной арки циклоиды х = 3(t - sint), y = 3(1 - cost),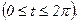 
.
301 - 320. Найти общее решение дифференциального уравнения.
301. 
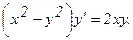
302. 
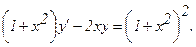
303. 
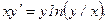
304. 
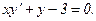
305. 
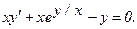
306. 
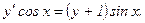
307. 
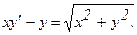
308. 
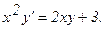
309. 
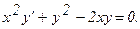
310. 
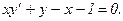
311. 
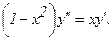
312. 
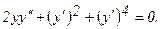
313. 
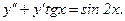
314. 
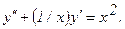
315. 
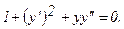
316. 
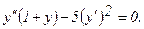
317. 
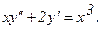
318. 
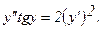
319. 
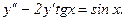
320. 
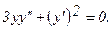
В задачах 321 - 330 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
321. у΄΄- еуу΄= 0, у(0) = 0, у΄(0) = 1.
322. у΄у΄΄= 2у, у(0) = 0, у΄(0) = 0.
323. уу΄΄= (у΄)2, у(0) = 1, у΄(0) = 3.
324. у3у΄΄= 3, у(1) = 1, у΄(1) = 1.
325. у΄΄-12у2= 0, у(0) =1/2, у΄(0) = 1.
326. 2у΄΄=е4у, у(0) = 0, у΄(0) = ½.
327. (у – 2)у΄΄ = 2(у΄)2, у(0) = 3, у΄(0) = 1.
328. 2уу΄΄= 3 + (у΄)2, у(1) = 1, у΄(1) = 1.
329. у΄΄=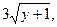 
у(2) = 0, у΄(2) = 2.
330. (у + 1)2у΄΄= (у΄)3, у΄(0) = 1.
331 - 340. Найти частное решение дифференциального уравнения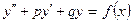 
, удовлетворяющее начальным условиям у(0)=у0,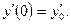 
331. 
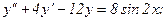
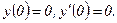
332. 
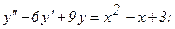
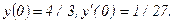
333. 
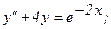
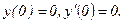
334. 
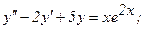
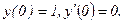
335. 
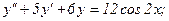
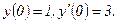
336. 
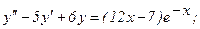
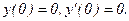
337. 
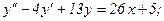
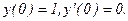
338. 
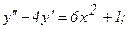
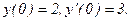
339. 
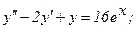
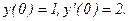
340. 
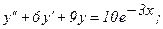
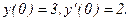
В задачах 341 - 350 даны линейные неоднородные дифференциальные уравнения второго полрядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.
341. y΄΄-2y΄-8y=16x2+2, y(0)=0, y΄(0)=5.
342. y΄΄+4y=3cos x, y(0)=1, y΄(0)=2.
343. y΄΄-y΄-2y=3e2x, y(0)=2, y΄(0)=5.
344. y΄΄-2y΄=2x+1, y(0)=1, y΄(0)=1.
345. y΄΄-2y΄+y=9e-2x+2x-4, y(0)=1, y΄(0)=1.
346. y΄΄-4y=4sin 2x, y(0)=2, y΄(0)=7.
347. y΄΄+y΄=3cos x – sin x, y(0)=0, y΄(0)=1.
348. y΄΄-y΄-6y=6x2-4x-3, y(0)=3, y΄(0)=5.
349. y΄΄-3y΄=3e3x, y(0)=2, y΄(0)=4.
350. y΄΄-4y΄+5y=5x – 4, y(0)=0, y΄(0)=3.
351 - 360. Дана система линейных дифференциальных уравнений с постоянными коэффициентами
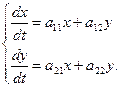
Требуется найти общее решение системы.
351. 
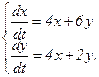
353. 
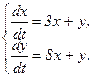
355. 
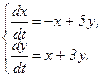
357. 
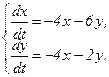
359. 
352. 
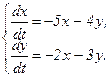
354. 
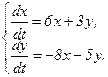
356. 
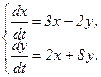
358. 
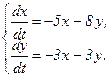
360. 
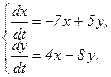
Date: 2015-04-23; view: 624; Нарушение авторских прав