Спин электрона. Сложение моментов

В 1920 г. П.Л. Капица и Н.Н. Семенов опубликовали в Журнале Русского Физико-Химического общества статью под названием «О возможности экспериментального определения магнитного момента атома», в которой было предложено пропускать молекулярный или атомный пучок через неоднородное магнитное поле. В неоднородном поле на магнитный момент действует сила пропорциональная ∂В/∂z (В — магнитное поле, а направление z перпендикулярно направлению движения пучка), и под действием этой силы произойдет отклонение движущихся частиц, так что если магнитные моменты не имеют

выделенной ориентации в пространстве (сейчас мы бы сказали, что имеем дело с пучком неполяризованных частиц), то на экране (фотопластинке) появится широкая полоса. Максимальное отклонение частиц будет соответствовать величине их магнитного момента. В конце статьи указывалось, что опыты такого рода начаты. Увы, эти эксперименты так и не были сделаны — в трудное послереволюционное время нельзя было достать соответствующие материалы и оборудование. Однако приведенные в этой статье расчеты показали, что опыт такого рода вполне реален — в магнитном поле с градиентом

dB/dz = 3 • 10⁴ Гс/см =300Tc/m отклонение должно составлять порядка 2 см.

Совершенно не зная о работе Капицы и Семенова, именно такой эксперимент провели в 1922 г. О. Штерн и В. Герлах. Вначале эти опыты проводились с пучками атомов серебра, а затем и других атомов, в том числе водорода. Схема экспериментов Штерна-Герлаха и одна из полученных ими фотографий распределения атомов после прохождения магнитного поля показаны на рис. 6.8.

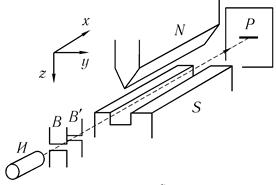
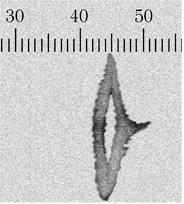
Рис. 6.8

Пучок атомов из источника И формируется двумя горизонтальными щелями B, В', проходит через отклоняющее магнитное поле и падает на фотопластинку Р. Магнитное поле создается электромагнитом, один полюс которого плоский, а другой сделан в виде ножа. Вблизи ножа поле имеет практически только z-компоненту, величина которой B_z очень сильно зависит от z-координаты. Сила, действующая на магнитный момент в таком

поле, равна

F_z = μ_z(dB_z/dz). (6.29)

Полученные Штерном и Герлахом результаты обладают двумя особенностями, полностью противоречащими классическим воззрениям:

1. Нет непрерывного распределения атомов по вертикали, а наблюдается

дискретность, т. е. возможны лишь некоторые из состояний.

2. В некоторых случаях наблюдалось расщепление пучка лишь на две компоненты.

Чего можно было бы ожидать, например, в случае водорода? Если атомы водорода находятся только в s-состоянии (l = 0), то никакого расщепления пучка вообще не должно быть, поскольку их магнитный момент в этом состоянии равен нулю. Если же атомы водорода находятся в p-состоянии (l = 1), то следовало ожидать расщепления на три компоненты, соответствующие трем возможным проекциям магнитного момента на ось z, т. е. состояниям со значениями магнитного квантового числа m_l = 0, ± 1. В то же время, эксперимент показал, что пучок расщепляется лишь на две компоненты. А это свидетельствует о наличии у атомов водорода еще какого-то момента импульса, назовем его s, равного 1/2.

В 1925 г. Дж. Уленбек и С. Гаудсмит, анализируя строение оптических спектров (мы уже говорили о трудностях интерпретации дуплетов в спектрах щелочных металлов), пришли к выводу о наличии у электрона собственного механического момента, равного ћ/2 (соответственно, магнитное квантовое число m_s = ±1/2), и назвали его спином. Это название происходит от английского слова spin, означающего вращение. Уленбек и Гаудсмит исходили из грубой классической модели электрона в виде вращающегося заряженного шарика. Конечно, в квантовой механике, как мы это неоднократно подчеркивали, нельзя говорить ни о каком вращении электрона.

Наличие у него собственного механического момента импульса (спина) есть

чисто квантовое явление. Собственным моментом импульса обладают также

и другие элементарные частицы, в частности — нейтрон, протон и т. д.

Еще одной неожиданностью результатов опытов Штерна и Герлаха явилось значение магнитного момента электрона, которое легко вычислить из величины расщепления. Оказалось, что проекция магнитного момента электрона на выделенную ось, если ее записать аналогично орбитальному движению (6.24), равна

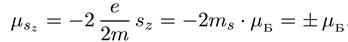. (6.30)

Таким образом, проекция спинового магнитного момента электрона равна

одному магнетону Бора. Для спина оказалось иным (вдвое большим!) гиромагнитное отношение, или другими словами, g-фактор электрона равен 2. Однако, точные измерения последнего показали, что на самом деле это равенство — приблизительное. Современная величина g-фактора равна

(1/2) g(e^-) = 1,001159 652 188 4(43). (6.31)

Следует отметить, что опыт Штерна-Герлаха на электронах невозможен, поскольку на движущиеся электроны, в силу их малой массы, действует не только градиент магнитного поля, но и само поле (сила Лоренца), и при этом оказывается, что смещение электронного пучка в результате действия силы Лоренца сравнимо со спиновым расщеплением.

К изучаемому нами классу явлений относятся также опыты А. Эйнштейна

и В. де Гааза 1915 г.), которые мы и рассмотрим (рис. 6.9).

В этих экспериментах образцы парамагнитных или ферромагнитных веществ в форме цилиндриков подвешивались на тонкой нити внутри соленоида. Пропускание тока сопровождалось вращением цилиндра, что давало

возможность определить связь между механическим и магнитным моментом вещества. 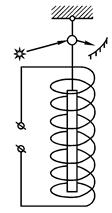Рис. 6.9

Вращение цилиндра при включении магнитного поля обусловлено тем, что магнитные моменты атомов μ ориентируются вдоль поля. Это ведет к изменению суммы их механических моментов L, и по закону сохранения момента импульса цилиндр закручивается.

Как было показано в более поздних работах С. Барнетта, Дж. Стюарта и других, для образцов из Fe, Ni, Co гиромагнитное отношение

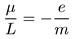
(6.32)

т. е. оказалось вдвое больше, чем должно было быть для магнитного и механического моментов, связанных с орбитальным

движением электронов (6.24). Следовательно, магнетизм у этих веществ (ферромагнетиков) имеет спиновое происхождение, т. е. имеет чисто квантовомеханическую природу.

Электрон в атоме, кроме спинового, может обладать также орбитальным моментом, поэтому естественно возникает вопрос о том, по какому правилу складываются моменты в квантовой механике. Угловые моменты — векторные величины, и складываться они должны по правилам сложения векторов.

Рассмотрим для простоты систему, состоящую только из двух частиц, имеющих орбитальные моменты l ₁ и l ₂. Пусть их суммарный момент равен L (рис. 6.10). Отметим, что если система состоит из многих частиц, то результирующий момент находится путем последовательного сложения двух векторов. Квантовый характер угловых моментов проявляется в квантовании как самой их абсолютной величины, так и их проекций. Для

суммарного момента это означает следующее:

|L|² = ћ²L(L + l) (6.33)

L_z = ћm_L L = 0, 1, 2, 3,

m_L = 0, ±1, ±2, ±L.

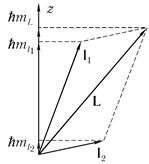
Рис. 6.10

Надо помнить, что у вектора L можно одновременно определить только его квадрат и проекцию момента на одну из координатных осей (мы выбираем ось z). Наша

задача — найти связь между квантовыми числами L и m и квантовыми числами складывающихся векторов l₁ и m_l1, l₂ и m_l2. Для этого рассмотрим проекции моментов на ось z (рис. 6.10).

Наибольшее возможное значение орбитального квантового числа L равно

наибольшему значению m_L, т. е.

L_max = m_Lmax = m_l1max + m_l2max = l₁ +l₂ (6.34)

Значение L минимально, когда проекции m_l1, m_l2 максимальны, но имеют разные знаки. Из рис. 6.10 ясно, что

L_min= l₁ - l₂ (6.35)

Но поскольку отрицательные значения L бессмысленны, то вместо (6.35)

выражение для L_min следует писать в виде

Lmin = |l₁ -1₂|. (6.36)

Это совсем не значит, что L_min соответствует антипараллельной ориентации векторов l₁ и l₂, a L_max — их параллельной ориентации, поскольку ни один из этих векторов не может быть направлен строго по какой-либо оси в силу соотношения неопределенностей.

Итак, возможные значения квантового числа суммарного момента лежат

в диапазоне

|l₁ -1₂| <L <l₁ +1₂, (6.37)

следовательно, L может принимать 2l₂ + 1 значений, если l₁ > l₂, и 2l₁ + 1

значений, если l₂ > l₁.

Но этим не ограничивается полное число возможных состояний системы

из двух частиц с моментами l₁ и l₂. Дело в том, что для каждого L (но

разных m_l) имеется 2L + 1 различных проекций (различных ориентации в

пространстве), поэтому полное число возможных состояний системы равно

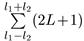(6.38)

h+h

Это арифметическая прогрессия с разностью, равной 2 и общим

числом членов (2l₂ + 1), ее сумма есть

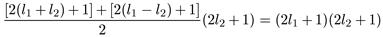
Это соотношение можно получить и иначе: число возможных состояний

для первой частицы равно (21₁+ 1), для второй — (2l₂ + 1), а для системы двух независимых частиц число состояний просто равно произведению возможных состояний каждой частицы, т. е. (21₁+ 1) (2l₂ + 1).

Итак, квантовомеханические векторы можно складывать так же, как обычные, но модуль любого из них равен ћ/√(l(l + 1)). Полученный результат называется квантовым правилом сложения угловых моментов. По этому же правилу находится суммарный момент частицы, если она участвует одновременно в двух вращениях.

Теперь можно перейти к вопросу о полных механическом и магнитном моментах электрона. В силу наличия у электрона как спинового, так и орбитального моментов, полный механический момент равен их сумме

j = l + s. (6.39)

Квантовое число j полного момента

j = |l±s| = |l±1/2|. F.40)

Естественно, как подчеркивалось выше, длина вектopa j

|j| = ћ/√(j(j + 1)). Jj_z = ћm_j. (6 41)

причем m_j принимает 2j + 1 значений.

Для суммарного магнитного момента ситуация резко осложняется из-за разных гиромагнитных отношений для спинового и орбитального моментов, и

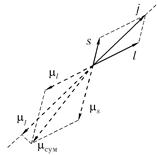
Pис.6.11. диаграмма сложения орбитального l и спинового s моментов электрона и соответствующих магнитных моментов μ_l, μ_s

в результате суммарный магнитный момент оказывается непараллельным суммарному механическому моменту (на рис. 6.11 изображена диаграмма сложения орбитального l и спинового s моментов электрона и соответствующих магнитных моментов μ_l, μ_s

механические моменты измеряются в единицах ћ, а магнитные — в магнетонах Бора). Следует обратить внимание на то, что величина вектора μ_l, равна величине вектора 1, а длина вектора μ_s вдвое больше, чем s.

Поэтому вводится специальный коэффициент — так называемый фактор Ланде, который есть не что иное, как коэффициент пропорциональности

между j и μ_j:

μ_j = -g_л μ _Bj. (6.42)

Это — то же гиромагнитное отношение, но не для частиц, а для атомных электронов. Заметим, что (6.42) — соотношение между проекцией суммарного магнитного момента μ _сум на j и величиной вектора j, а не соотношение между этими векторами.

Конкретное выражение для фактора Ланде через значения j, l и s легко

получить. В самом деле, с учетом того, что спиновый g-фактор равен 2,

из (6.39) следует:

- μ_j = μ _Bl + 2μ_s s. (6.43)

Соответственно, проекция суммарного магнитного момента μ_j на вектор j

равна

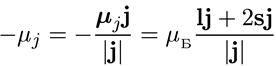
(6.44)

Значит

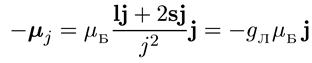
(6.45)

Мы получили соотношение между проекцией магнитного момента μ_j и вектором j. Отсюда можно получить выражение для фактора Ланде

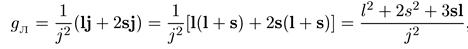, (6.46)

или

g_л |j|² = |l|² + 2| s |² + 3sl. (6.47)

Это — просто векторное соотношение. В операторном виде оно записывается

как

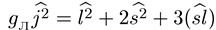. (6.48)

Операторное равенство означает и равенство средних значений, т. е.

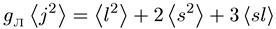. (6.49)

Первые два члена в правой части равенства (6.49) легко находятся по общему квантовомеханическому правилу для квадрата вектора (для любого вектора М имеем

М² = М(М + 1)),

а среднее значение третьего члена вычислим, исходя из следующих соотношений:

j = 1 + s -> j² = s² + l² + 2s l -> sl =(l/2)(|j|²-|s|²-|l|²). (6.50)

Значит

(sl) = (l/2)[j(i + 1) - s(s + 1) – 1(l + 1)], (6.51)

и окончательно имеем

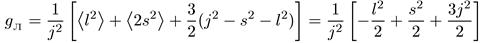
или

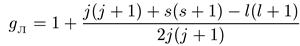(6.53)

Date: 2015-05-19; view: 1161; Нарушение авторских прав