Тонкая структура спектра атома водорода

Как указывалось в предыдущем параграфе, наличие спина у электрона приводит к расщеплению энергий состояний с опреленным значением l (т. е. момента импульса, связанного с орбитальным движением электрона) за счет спин-орбитального взаимодействия. Его происхождение качествено может быть легко понято, если иметь в виду, что собственный магнитный момент электрона, связанный с его спином, взаимодействует с магнитным полем орбитального тока. Можно рассуждать по-иному: в системе координат электрона, движущегося в кулоновском поле ядра, возникает магнитное поле, с которым взаимодействует собственный магнитный момент электрона. Энергия такого взаимодействия зависит от ориентации магнитного момента относительно направления поля, т. е. от его проекции на это направление. А так как проекция магнитного момента (вместе с проекцией спина) может принимать два значения, то для любого l мы получаем расщепление на два состояния, соответствующие двум возможным значениям квантового числа полного момента j = l±1/2. Исключение составляет лишь состояние с l = 0, для которого j принимает только одно значение: j = 1/2. Таким образом,

наличие спина у электрона приводит к возникновению поправки к полной

энергии атома водорода (см. (5.44)), зависящей от квантового числа j. Эта

поправка невелика, она такого же порядка, что и релятивистская поправка.

Последовательный квантовомеханический расчет, учитывающий оба типа

поправок, дает:

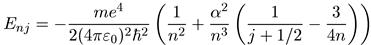
(6.54)

где m— приведенная масса электрона и протона,

α = е²/(4πε₀ћc) = 1/137

—уже встречавшаяся нам постоянная тонкой структуры,

определяющая величину расщепления уровней по квантовому числу j. Само расщепление, описываемое (6.54), носит название тонкой структуры спектра атома водорода. Подчеркнем еще раз, что поправка за счет спин-орбитального взаимодействия мала: как следует из (6.54), ее отношение к основному члену порядка α², т. е. порядка (1/137)².

Как же выглядит спектр атома водорода с учетом тонкой структуры?

Для классификации электронных состояний обычно применяют спектроскопические обозначения, записываемые в виде nlj, где n — главное квантовое число, l — орбитальное квантовое число в буквенном обозначении (см. §. 6.2), j — квантовое число полного момента импульса или, как его часто называют, полного углового момента.

Основное состояние (главное квантовое число n = 1, а орбитальное l = 0) не расщепляется (а лишь слегка смещается вниз по энергии), поскольку j принимает только одно значение, равное 1/2. Следующее состояние, для которого n = 2, а l может принимать значения 0 и 1, расщепляется по энергии на два, т. к. здесь j может быть равно 1/2 и 3/2. При этом значение j = 1/2 получается в результате сложения спина электрона как с орбитальным моментом l= 0 (состояние 2s_1/2) так и с l = 1 (состояние 2р_1/2), в то время как j = 3/2 может получиться лишь от сложения с l = 1 (состояние 2p_3/2). Уровень энергии, соответствующий n = 3, расщепляется на три соответственно трем значениям, которые может принимать квантовое число j, а именно: 1/2 (состояния 3s_1/2 и 3p_1/2), 3/2 (3р_3/2 и 3d_3/2) и 5/2 (состояние

3d_5/2). И так далее.

Согласно (6.54) уровни тонкой структуры атома водорода, соответствующие определенному значению главного квантового числа, двукратно вырождены по l (за исключением уровня с максимальным значением j). Например, состояния 2s_1/2 и 2р_1/2 должны иметь одинаковую энергию. На самом деле их энергии различаются: энергия состояния 2s_1/2 располагается несколько выше, чем энергия 2р_1/2 (хотя и ниже энергии уровня 2p_3/2). Это расщепление уровней, составляющее порядка 1/10 тонкого расщепления, получило название лэмбовского сдвига по имени У. Лэмба, окончательно

установившего в 1947 г. его существование. Причиной лэмбовского сдвига является взаимодействие электрона с флуктуационным электромагнитным полем, или, как принято говорить в квантовой электродинамике, с флуктуациями вакуума. Рассмотрение данного эффекта выходит за рамки нашего курса. Можно лишь отметить, что современная квантовая электродинамика дает превосходное количественное описание такого расщепления.

Отметим, что с учетом спина электрона появляется новая степень свободы, а следовательно, и новое квантовое число m_s (ћm_s — проекция спина на выделенное направление), принимающее значения ±1/2. Таким образом, состояние электрона в атоме водорода можно характеризовать четырьмя квантовыми числами: n, l, m_l, m_s. Однако, поскольку орбитальный момент и спин складываются в полный момент (от которого зависит энергия состояния), то состояние атома водорода удобно описывать с помощью другого набора квантовых чисел, а именно: n, l, j, m_j, где m_j — квантовое число проекции полного момента импульса, пробегающее 2j + 1 значений (- j, -j + 1,..., j - 1, j). Энергия состояния зависит от n и j, зависимость от l появляется при учете лэмбовского сдвига. Состояния вырождены по m_j.

Физический смысл этого вырождения состоит в следующем: при отсутствии физически выделенного направления все ориентации момента импульса в пространстве равноправны.

Коротко остановимся на правилах отбора для электромагнитных переходов (т. е. переходов из одного состояния в другое с испусканием или поглощением фотона). Для систем размеров порядка атомных наиболее вероятным является дипольное электромагнитное излучение и поглощение, которое, как показывает расчет, может происходить лишь при определенных соотношениях между квантовыми числами начального и конечного состояний, а именно: реализуются только такие лектромагнитные переходы, при которых изменения квантовых чисел принимают следующие значения:

Δj = 0, ±1; Δm_j = 0, ±1; Δl = ±1; Δm_l = 0, ±1; Δm_s = 0. (6.55)

Правила отбора (6.55) справедливы не только для водорода, но и для дородоподобных атомов. Отметим, что для многоэлектронных атомов (отличных от водородоподобных) также можно получить правила отбора, для которых (6.55) являются частным случаем. Они будут подробнее рассмотрены в дальнейшем.

ГЛАВА 7

ПРИНЦИП ЗАПРЕТА ПАУЛИ. ПЕРИОДИЧЕСКАЯ ТАБЛИЦА

Date: 2015-05-19; view: 1035; Нарушение авторских прав