Эффект Зеемана

Теперь у нас полностью готова база для рассмотрения поведения атома в магнитном поле. Прежде всего обратимся к влиянию внутренних полей. Со спиновым механическим моментом электрона s связан магнитный момент

μ _s = -(e/m) s. (8.9)

Это означает, что при наличии магнитного поля произойдет взаимодействие спина с последним, и появится дополнительная «магнитная» энергия. На примере атома водорода мы видели, что существование магнитного момента электрона приводит к появлению спин-орбитального взаимодействия, в результате которого уровни с l ≠ 0 расщепляются по энергии на два подуровня

с j = l ±1/2 — как говорят, возникает тонкая структура уровней. Такое расщепление мало по сравнению с расстоянием между уровнями с разными n(см. формулу (6.56)). Сразу отметим, что энергия спин-орбитального взаимодействия, а значит и величина расщепления, зависят от l; это хорошо видно из той же формулы (6.56).

n=2

На рис. 8.2 приведен пример тонкой структуры водородоподобного атома с n = 2: уровень с l = 1 ращеплен на два с j=l±s = l ±1/2, спектроскопические обозначения которых Р_3/2 Р_1/2 (см гл 6)

Спин-орбитальное взаимодействие снимает

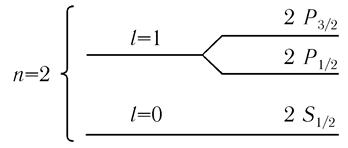
Pис. 8.2 пример тонкой структуры водородоподобного атома с n = 2: уровень с l = 1 ращеплен на два с j=l±s = l ±1/2, спектроскопические обозначения которых Р_3/2 Р_1/2

вырождение уровней по l (вспомним, что в чисто кулоновском поле энергия

зависит только от n, 0 < l < n-1, с каждым l связано (21 + 1)-кратное вырождение по m_l, итого с учетом спина получается 2n²-кратное вырождение или 2n²-мультиплетность уровня). Мы уже упоминали хорошо известный пример снятия такого вырождения у натрия, в спектре которого наблюдается желтый дублет с длинами волн 5890 и 5896 А⁰.

Взаимодействие спина с магнитным моментом ядра приводит к появлению сверхтонкой структуры атомных спектров. Интервалы этого расщепления чрезвычайно малы: их масштаб на два-три порядка меньше масштаба расщепления, обусловленного тонкой структурой. Поэтому сверхтонкая структура должна рассматриваться для каждой из компонент тонкой структуры в отдельности. Если спин ядра обозначить через I, а электронной оболочки — через J, то полный момент атома и ядра будет равен F = J + I, и F пробегает значения

F = J + I, J + I - 1,..., | J – I|. (8.10)

Соответственно, число компонент сверхтонкой структуры уровня с данным J равно 2I + 1 (если J > I) или 2 J + 1 (если J < I).

Перейдем теперь к рассмотрению поведения атома во внешнем магнитном поле — эффекту Зеемана. Это явление — расщепление спектральных линий в магнитном поле — было открыто голландским физиком П. Зееманом в 1896 г. С внешним магнитным полем взаимодействуют как орбитальный, так и спиновый магнитные моменты электронов. Кроме того нужно иметь в виду, что эти магнитные моменты взаимодействуют между собой (знакомое нам спин-орбитальное взаимодействие). В зависимости от относительной величины указанных взаимодействий различают два случая: слабого магнитного поля и сильного магнитного поля.

В первом случае взаимодействие внешнего магнитного поля с орбитальным и спиновым магнитными моментами электронов существенно меньше спин-орбитального взаимодействия, и в результате расщепление уровней за счет внешнего магнитного поля оказывается меньшим, чем расщепление, обусловленное тонкой структурой. Этот случай носит название сложного эффекта Зеемана, поскольку в сильных полях структура спектра оказывается намного проще (как мы увидим чуть позже). Дополнительная энергия

в магнитном поле в данном случае равна

Е_в = -(μВ) = gμ_Б(J В) = gμ_Бm_j В. (8.11)

Здесь m_j определяет проекции вектора J на направление внешнего поля В и принимает

2 J + 1 значений, т. е. все зависит от взаимной ориентации векторов J и В. Расщепление уровней оказывается эквидистантным, а сама величина расщепления линейно растет с полем. О таком случае говорят, что магнитное поле снимает вырождение уровней по m_j. Поскольку внешнее расщепление меньше внутреннего (тонкой структуры), то картина слегка расщепленных спектральных уровней остается практически такой же, как

и без поля.

Хотя расщепление одного уровня является эквидистантным, значения фактора Ланде g, вообще говоря, различны у разных уровней, что приводит к возникновению сложного расщепления линий перехода. При этом существенное значение имеют правила отбора для излучения. Классический пример эффекта Зеемана — поведение желтого дублета натрия в магнитном поле (сам дублет есть проявление тонкой структуры уровней). Основное состояние натрия 3²S_1/2, a выше расположены два возбужденных состояния

3²P_1/2 и 3²Р_3/2. На рис. 8.3 стрелками показаны переходы, разрешенные правилами отбора.

В чисто кулоновском поле энергия зависит только от квантового числа n и поэтому, казалось бы, не должно быть разницы в энергии уровней с разными l. Однако реально это справедливо лишь для водорода и водородоподобных атомов, а в натрии внутренние электроны экранируют поле ядра, таким образом, для p-электронов заряд ядра как бы меньше, чем для s-электронов, и они располагаются несколько выше. Из-за спин-орбитального взаимодействия p - уровень расщепляется на два (тонкая структура), и в спектре излучения появляется желтый дублет. Величина спин-орбитального расщепления у натрия равна U_LS = 2 • 10^-3 эВ, а во внешнем поле (B=10² Tl) Н = 10³ кЭ

1 Э= 10³/(4π) А/м) оно, согласно формуле (8.11), порядка (в системе Си)

ΔU_B = μ₀ μ_ъB = 4π • 10^-7 • 9,3 • 10^-24 • (10⁶/4π) =

= 10^-24 Дж = 6 • 10^-6 эВ << U_LS, (8.12)

т. е. поля такого порядка являются слабыми.

Во внешнем поле уровень 3²Р_1/2 расщепляется, как и уровень 3²S_1/2 на два подуровня с проекциями m_j = ±1/2, а уровень 3²Р_з/2 — на 4 подуровня с m_j =3/2, 1/2, -1/2, -3/2 (при этом уровень с m_j =3/2 расположен выше всех, а с m_j = - 3/2 — самый низкий, что непосредственно следует из формулы (8.11)). Всего в слабом магнитном поле наблюдается 10 переходов. В силу правил отбора (Δm_s = 0, Δm_L = 0, ±1, Δm_j =0, ±1) не могут происходить переходы с m_j = 3/2 на уровень m_j = - 1/2 и с m_j = - 3/2 на m_j = 1/2.

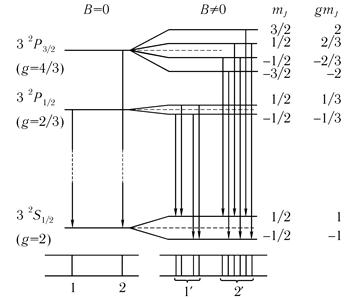
Рис. 8.3 стрелками показаны переходы, разрешенные правилами отбора

Еще раз подчеркнем: так много линий наблюдается из-за того, что у разных уровней разная величина расщепления. Поэтому, в частности, переходы с уровня 3²Р_1/2 на 3²S_1/2

между подуровнями с m_j (1/2 —> 1/2) и (-1/2 —> -1/2) по энергии не равны. Действительно, у всех рассмотренных нами уровней натрия значения фактора Ланде разные:

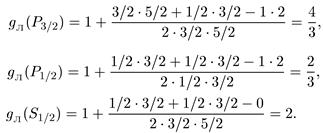
Теперь рассмотрим простой эффект Зеемана, наблюдаемый в сильном магнитном поле. Здесь термин «сильное поле» означает, что энергия спин- орбитального взаимодействия U_SL намного меньше, чем энергия взаимодействия как спинового, так и орбитального магнитных моментов с внешним полем, т. е. U_SL << U_SB,U_LB. В случае слабого поля мы классифицировали состояния точно так же, как и без поля, а в данном случае этого делать

уже нельзя. Теперь мы считаем величину U_SL практически равной нулю, т. е. ренебрегаем данным взаимодействием. Последнее означает, что оператор энергии не зависит от ориентации спинового и орбитального моментов, а следовательно, он не зависит и от суммарного вектора J = L + S. Остается зависимость энергии лишь от проекций векторов L и S на вектор В, т. е. только от квантовых чисел m_L и m_s. Для этого случая существует

жаргонное выражение: говорят, что в сильном поле «разрывается LS-связь».

Итак, учитывая, что g_L = l, g_s=2, магнитная часть энергии в сильном поле равна

U_B = g_L μ_ъ m_LB + g_s μ_ъ m_sB = μ_ъB

Теперь уже «нет» спин-орбитального расщепления, уровень 3²Р расщепляется на 5 компонент с m_L + 2m_s = 2, 1, 0, -1, -2, а уровень 3²S — на 2, как

это показано на рис. 8.4.

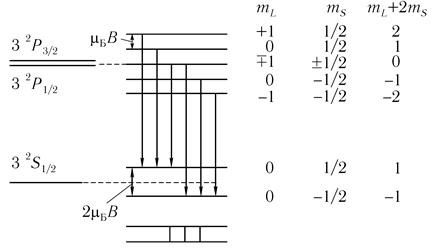
Рис. 8.4 Теперь уже «нет» спин-орбитального расщепления, уровень 3²Р расщепляется на 5 компонент с m_L + 2m_s = 2, 1, 0, -1, -2, а уровень 3²S

Покажем, что в сильном поле всегда будут наблюдаться лишь 3 линии.

Пусть имеется два уровня с энергиями E₀₁ и E₀₂, характеризующихся квантовыми числами L1, L2, S1, S2. Разность энергий этих уровней в сильном

поле равна

ΔU_B = [Е₀₂ + μ_ъB(m_L2 + 2m_S2)] - [Е₀₁ + μ_ъB(m_L1 + 2m_s1)]. (8.15)

Так как по правилам отбора возможны переходы только между уровнями с

m_s1 = m_s2

то

ΔU_B = (E₀₂ – E₀₁) +μ_ъB(m_L2 – m_L1) (8.16)

Ho Δm_L = 0, ±1, а значит, в спектрах излучения в сильном поле всегда будут наблюдаться лишь три линии — одна несмещенная и две смещенные на ± μ_ъB. Вот почему эффект Зеемана в сильном магнитном поле называется простым.

В заключение рассмотрим, как будет поляризован свет при простом эффекте Зеемана. Когда наблюдение ведется вдоль приложенного магнитного поля, эффект Зеемана называют продольным. При этом, поскольку Δm_s = = 0, a Δm_L = 0, ±1, уносимый фотоном момент равен 1 (дипольное излучение), и оказывается, что смещенные компоненты имеют круговую поляризацию (у них Δm_L = ±1). Несмещенная компонента вообще видна не будет, т. к. для нее Δm_L = 0, а фотона с m_z = 0 не существует.

В поперечном эффекте Зеемана (наблюдение поперек магнитного поля) несмещенная линия — это просто линейно поляризованный свет, а циркулярно-поляризованные смещенные линии также будут выглядить как линейно-поляризованные волны. В результате при наблюдении в перпендикулярном направлении мы увидим три линейно-поляризованных волны. Таким образом, энергетические уровни частиц (любых — это могут быть и ядра, и молекулы), обладающих ненулевыми магнитными моментами, во

внешнем магнитном поле испытывают зеемановское расщепление. Если облучать такие частицы внешним электромагнитным излучением с частотой, равной энергии переходов между подуровнями:

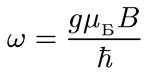, (8.17)

то будет происходить резонансное поглощение излучения. В зависимости от сорта частиц это может быть ЭПР — электронный парамагнитный резонанс, либо ЯМР — ядерный магнитный резонанс. В последнем случае масштаб измерения магнитных моментов определяется не магнетоном Бора, а так называемым ядерным магнетоном

μ_я = eћ/2m_p,

где m_р — масса протона, т. е. ядерный магнетон примерно в 1800 раз меньше магнетона Бора: он равен

5,05 • 10 ^-27 Дж/Тл = 5,05 • 10^-24 эрг/Гс.

Обычно опыты проводят так, что частота генератора, создающего переменное электромагнитное поле, держится постоянной, а меняется внешнее магнитное поле В. В образце энергия атомов с μ ≠ 0 зависит от ориентации магнитных моментов. Если приложено внешнее поле, то после установления теплового равновесия, в соответствии с больцмановским распределением заселенности уровней, число частиц с моментами, ориентированными вдоль поля, оказывается больше числа частиц с противоположной ориентацией магнитных моментов. Таким образом результирующий магнитный момент

образца становится отличным от нуля, т. е. образец намагничивается. Этот эффект получил название «парамагнитный резонанс», он впервые наблюдался Е.К. Завойским в 1944 г.

ГЛАВА 9

Date: 2015-05-19; view: 1859; Нарушение авторских прав