Пространственное квантование. Энергия физической системы в зависимости от формы потенциальной кривой может иметь либо непрерывный

Энергия физической системы в зависимости от формы потенциальной кривой может иметь либо непрерывный, либо дискретный спектр. В то же время другая физическая величина — момент импульса L — для любой системы может принимать только определенный, дискретный ряд значений.

Момент импульса характеризует вращательное (угловое) движение. При изучении такого движения удобно пользоваться полярной системой координат (рис. 6.1). В этой системе положение точки характеризуется: расстоянием r от начала отсчета; полярным углом θ между полярной осью z и радиусом- вектором r; азимутальным углом φ, отсчитываемым в плоскости ху от оси х.

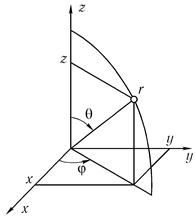
Рис. 6.1

Волновая функция ψ_Lz, описывающая состояние с определенным значением проекции L_z на ось z в значительной мере аналогична плоской волне де Бройля:

exp(i(p_x/ћ)z)

роль координаты играет азимутальный угол φ (угол поворота вокруг оси z), а роль проекции импульса — проекция момента импульса на эту ось; оператор проекции момента импульса имеет вид

L_z = -iћ(∂/∂φ),

и, таким образом,

ψ_Lz ~ e^i(Lz/ћ)φ

При этом по смыслу угловой переменной углы φ и φ + 2π описывают одно и то же положение частицы относительно оси z: если систему повернуть вокруг оси z на угол 2π, то она перейдет сама в себя. Поэтому волновые функции должны удовлетворять условию периодичности

ψ_Lz (φ)= ψ_Lz (φ+ 2π). (6.2)

Как следует из (6.1), это условие выполняется лишь в том случае, если L_z/ћ

принимает целочисленные значения. Следовательно, L_z, в отличие от проекции импульса p_z, может принимать только дискретные значения:

L_z = m_lћ, где m_l = 0, ±1, ±2,... (6.3)

Таким образом, проекция момента количества движения на любую ось квантуется и равна целому числу постоянных Планка (на рис. 6.2 дано схематическое изображение квантования проекции L_z момента импульса L на ось z).

Квантование проекции момента означает, что вектор квантового момента импульса не может иметь произвольного направления по отношению к любому фиксированному направлению в пространстве. Этот факт получил название пространственного квантования. Оно выглядит крайне необычно: поскольку направление оси z можно выбрать произвольно, то проекции момента на два различных направления (z и z') квантуются одинаково.

Возможные значения проекции момента на оси х и у также определяются

формулой (6.3).

Может показаться, что квантование проекции L_z приводит к тому, что вектор L составляет лишь определенные углы с осью, как это схематично показано на рис. 6.2.

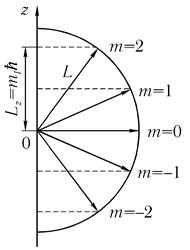
Рис. 6.2

Однако полученный результат имеет совсем другой смысл. Формула (6.3) показывает, что при измерении проекции момента импульса мы в результате опыта обязательно получим число, являющееся кратным ћ. Однако значение L_z до этого вовсе не должно быть равно целому числу ћ. До и после опыта ψ-функции вовсе не обязаны совпадать. Мы вправе лишь утверждать, что ψ-функция состояния, имевшегося до опыта, т. е. ψ-функция любого физического состояния, может быть представлена в виде суперпозиции собственных решений:

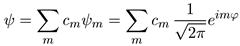
(6.4)

Система, описываемая такой ψ-функцией, не обладает определенной проекцией момента L. Вектор L может быть направлен произвольным образом, но при измерении L_z всегда будет найдено какое-то одно из т значений, входящих в сумму (6.4). Вероятность найти значение L_z = mћ определяется, как всегда, величиной |с_m|²

Рис. 6.3

Таким образом, вектор момента импульса не имеет определенного направления в пространстве. В этом смысле рис. 6.2 является условным. При фиксированном значении проекции момента на ось z вектор момента импульса как бы прецессирует вокруг этой оси, из-за чего проекции L_x и L_y не имеют определенных значений (рис. 6.3). В данном случае мы снова сталкиваемся с действием квантовомеханического принципа неопределенностей.

Проекция момента не может быть больше его абсолютного значения. Поэтому при фиксированной величине модуля момента возможные значения числа m_l ограничены сверху числом l. Если l задано, то проекция момента может принимать 2l + 1 значений.

Найдем возможные значения момента импульса. Средние значения проекций L_x, L_y и L_z, как и любых других величин, могут иметь в данном состоянии определенные значения. Если никаких предварительных операций для фиксации проекции момента на какое-либо направление не производилось (нет выделенной поляризации частиц), то все направления равноправны и средние значения квадратов проекций момента импульса одинаковы:

<L_x²> = <L_y²> = <L_z²>. (6.5)

Это утверждение вместе с правилом квантования проекции момента (6.3) позволяет определить возможные значения квадрата момента импульса.

Среднее значение квадрата момента, как и в классической механике, равно сумме средних значений квадратов проекций. Учитывая равенство (6.5), получим

<L²> = <L_x²> + <L_y²> + <L_z²>

(6.6)

При любой ориентации момента его квадрат имеет одну и ту же величину.

Следовательно,

L² = < L ²> = 3<L_z²>. (6.7)

Все значения L_z равновероятны, если никакого отбора по возможным состояниям не производилось. Поэтому среднее значение <L_z²>равно сумме всех

2l + 1 возможных значений <L_z²> от lћ до -lћ, деленной на их полное число:

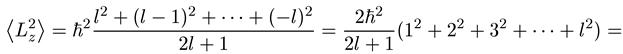
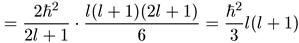
Здесь мы использовали известное выражение для суммы квадратов целых

чисел от 1 до l. Подставив полученное значение <L_z²> в (6.6), найдем

L² = ћ²l(l + l). (6.8)

Равенство (6.8) определяет закон квантования квадрата момента количества движения,

т. е. его длину.

Число m_l от которого зависят значения проекции момента, называется магнитным квантовым числом. Этот термин обусловлен тем, что, как мы увидим в дальнейшем, проекция магнитного момента, создаваемого движением заряженной частицы, пропорциональна проекции момента импульса этой частицы, определяемого числом m_l. Максимальное значение магнитного квантового числа m_max = l, а минимальное m_min= -l. Число l, определяющее возможные значения квадрата момента, называется орбитальным квантовым числом.

Отметим еще одно отличие квантового момента от классического. Максимальное значение проекции квантового момента ћl не равно модулю момента ћ√(l(l + 1)), а меньше его. Мы уже подчеркивали, что в силу соотношения неопределенностей у микрочастицы не могут быть одновременно известны проекции момента на две различные оси. Зафиксировав состояние с определенным L_z, мы вносим неопределенность в проекции L_x и L_y. В квантовой механике задание L² и одной из проекций момента импульса полностью

определяет вращательное состояние тела.

Date: 2015-05-19; view: 1046; Нарушение авторских прав