
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Допустимых значений энергии частицы
|
|
Константу С найдем из условия нормировки ψ-функции:
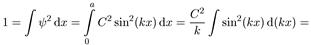
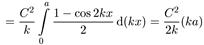 (5.6)
(5.6)
откуда следует, что С = √(2/а) и, таким образом, решение нашего уравнения
имеет вид
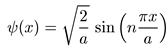 (5.7)
(5.7)
Здесь необходимо отметить, что в стационарном состоянии к не есть волновое число волны де Бройля, ибо ψ-функция в данном случае не является плоской волной. Дело в том, что у частицы нет определенного импульса, имеется лишь распределение по k, а в основном состоянии (n = 1) вообще Δр~р. В этом смысле р ≠ ћk, хотя к строго определено. Это и есть проявление корпускулярно-волнового дуализма. Мы уже подчеркивали, что в квантовой механике можно говорить лишь о полной энергии системы, но нельзя делить ее на кинетическую и потенциальную.
Посмотрим, как выглядит наше решение (волновая функция и ее квадрат) при разных n. На рис. 5.2 а изображена волновая функция частицы в одномерной
потенциальной яме с бесконечными стенками; рис. 5.2 б — вероятность нахождения частицы в пространстве (на этом рисунке масштаб энергий уровней не соблюден).
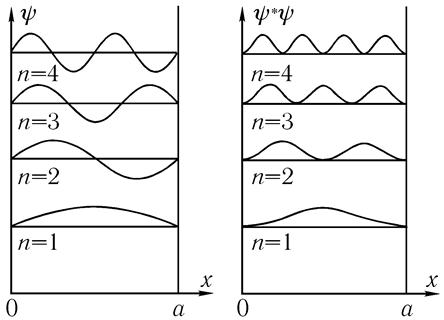
Рис. 5.2 а- Волновая функция частицы в одномерной
потенциальной яме с бесконечными стенками
б - вероятность нахождения частицы в пространстве (на этом рисунке масштаб энергий уровней не соблюден)
Из полученного результата можно сделать следующие выводы:
1. Энергия частицы Е в потенциальной яме не может быть произвольной,
она принимает ряд дискретных значений.
2. Наименьшая возможная энергия
Е1 = ћ2π2/(2mа2)
не соответствует «классическому» минимуму — дну ямы. Она называется нулевой энергией, и ее существование есть следствие принципа неопределенностей: ограничив частицу областью возможных значений координат (0, а), мы вносим разброс по импульсам, т. е. минимальная энергия всегда отлична от нуля.
Исходя из приведенных ранее соображений, — энергия основного состояния соответствует наименьшей возможной полной энергии нической системы, совместимой с принципом неопределенностей, — легко оценить энергию основного состояния частицы в прямоугольной яме ширины а с бесконечными стенками. В данном случае
Δх ~~ а,
а потому импульс частицы
р ~~ Δр ~ ћ/a.
Если отсчитывать, как это принято, энергию частицы от дна ямы, то ее минимальная энергия будет равна
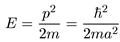
Что, естественно, совпадает с выражением (5.5) для энергии при n = 1.
3. Спектр возможных значений энергии частицы в прямоугольной яме с
бесконечными стенками квадратичный (Еn ~ n2).
4. Дискретность энергетических уровней с необходимостью приводит к
дискретности спектров излучения и поглощения энергии.
5. Как видно из рис. 5.2, по мере увеличения энергии (числа n) максимумы кривой |ф|2 располагаются все ближе и ближе и картина «сливается», становясь классическим равномерным распределением, при котором частица с равной вероятностью может находиться в любой точке от 0 до а. Это еще одна иллюстрация уже упоминавшегося критерия: классическая механика соответствует условию а >> λ, т. е. при длинах волн, много меньших размеров системы, в которой движется (локализована) частица, квантово- механические особенности частиц оказываются несущественными.
Рассмотренный нами случай потенциальной ямы с бесконечными стенками имеет скорее методическое, нежели практическое значение. Реально мы имеем дело с ямами со стенками конечной высоты, и, разумеется, наиболее интересен вариант, когда потенциальная яма не одномерна, а трехмерна.
Рассмотрим простой трехмерный случай, когда потенциальная яма сферически симметрична относительно некоторого силового центра. Это означает, что U = U(r), где r = |r|. Ограничимся нахождением только сферически симметричных решений — решений, зависящих только от r, т. е. при ψ= ψ(r). Тогда в уравнении Шредингера для нашего случая

(5.9)
радиальная часть лапласиана, записанного в сферических координатах, име-
имеет вид
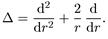
В отличие от одномерного уравнения, здесь появился новый член 2/r • d/dr.
Сделаем в (5.9) замену переменных: ψ= ξ/r. Тогда
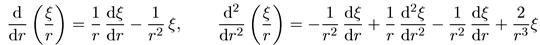
и мы имеем
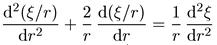
Получается, что наше уравнение для ф свелось к следующему уравнению
для функции?:
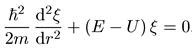 (5.11)
(5.11)
Это уравнение математически тождественно уравнению для одномерного движения, но с одним отличием — при r = 0 функция ξ(r) должна не только быть конечной, но и обращаться в нуль, так как в противном случае функция ψ = ξ/r обращалась бы в бесконечность при r = 0. Поэтому задача о движении частицы в трехмерном сферически симметричном потенциале эквивалентна одномерной задаче с потенциалом, определяемым выражением
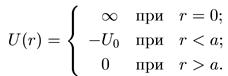
(5.12)
Нас будут интересовать состояния финитного движения, относящиеся к дискретному спектру энергий 0 < Е < U0. Так как функция U(x) является ступенчатой, то для решения задачи удобно разбить область изменения x, как мы это делали при решении задачи о прохождении частицы через потенциальный барьер, на два участка с постоянными значениями U.
В области 0 < х < а уравнение Шредингера имеет вид
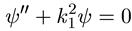 , (5.13)
, (5.13)

а в области вне ямы:
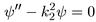
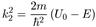
(5.14)
Общие решения этих уравнений можно записать в виде

(5.15)
где индексами 1 и 2 обозначены решения внутри и вне ямы соответственно.
Из граничного условия ψ1(0) = 0 следует, что а = 0. Чтобы волновая функция оставалась всюду конечной, необходимо соблюдение условия с = 0. И, наконец, из условия непрерывности волновой функции и ее производной по координате в точке х = а найдем
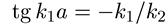
(5.16)
откуда получаем,
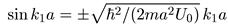
(5.17)
При выводе этого соотношения мы использовали тригонометрическое равенство
sin2 a = tg2a/(l + tg2 а)
и следующую из формул (5.13) и (5.14)
связь
к1 2 + к2 2 = 2mU0/h2.
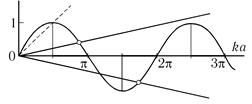
Pis 5.3
Изобразив графически левую и правую части последнего уравнения (рис. 5.3),
найдем точки пересечения прямых с синусоидой. При этом корни данного уравнения, отвечающие собственным значениям Е, будут соответствовать тем точкам
рис 5.3 пересечения, для которых tg (к1а) < 0, т. е. будут находиться в четных четвертях
окружности (эти участки оси абсцисс выделены на рисунке жирными отрезками).
Из графика видно, что корни уравнения (т. е. связанные состояния) существуют не всегда; пунктиром показано предельное положение прямой, соответствующей условию k1a = π/2. Именно этим условием определяется минимальное значение энергии частицы в яме конечной глубины — ее нулевая энергия, равная величине
 . (5.18)
. (5.18)
Стационарные уровни возникают только в том случае, если Е < U0. Поэтому уровни в потенциальной яме рассматриваемого типа возникают лишь при выполнении неравенства
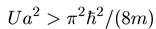 . (5.19)
. (5.19)
В левой части последнего неравенства стоят параметры потенциальной ямы, а в правой — только постоянные числа и универсальные постоянные. Если полученное нами условие не выполнено (потенциальная яма слишком узкая или слишком мелкая), в ней не помещается ни одного энергетического уровня. Иными словами, в таком случае, несмотря на то, что потенциал является для частицы притягивающим, связанного состояния не образуется.
Подобная ситуация реально встречается. Например, силы взаимодействия между двумя нейтронами являются силами притяжения, однако ядра, состоящего из двух нейтронов, в природе не существует. Аналогичным образом не существует и ядра, состоящего из двух протонов.
Следует отметить еще одно отличие классического и квантового поведения частицы в потенциальной яме. Согласно квантовой механике, частица, находящаяся в потенциальной яме со «стенками» конечной толщины (типа кратера вулкана), в результате туннельного эффекта может покинуть последнюю, даже если ее энергия меньше высоты стенок потенциальной ямы.
В этом случае говорят, что уровни энергии частицы являются квазистационарными, т. к. частица «живет» в таком состоянии конечное время. О подобных уровнях также говорят как о метастабилъных. Все уровни частицы в потенциале со стенками конечной толщины имеют конечную ширину, т. е. энергия такого состояния точно не определена (состояние не является строго стационарным); при этом ширина состояния зависит, естественно, от его энергии и формы потенциала.
Форма потенциальной ямы и ее размеры (глубина и ширина), определяемые физической природой взаимодействия частиц, могут быть различными.
Два частных случая формы потенциальных ям имеют очень большое значение в физике.
1. Кулоновская потенциальная яма
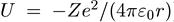
U = -Ze2/(4πе0r)),
описывающая притяжение атомного электрона ядром с зарядом Z.
2. Потенциал гармонического осциллятора (U = kх2/2), играющий важную роль в физике твердого тела, электромагнитного излучения, колебательных спектров молекул, являющийся одной из моделей ядерного потенпотенциала.
Для одномерного движения справедлива так называемая осцилляционная теорема: волновая функция ψ(x) дискретного спектра, соответствующая (n + 1)-у по величине собственному значению Еn, обращается в нуль (при конечных значениях х) n раз. Примером может служить рассмотренная выше задача о частице в прямоугольной яме (см. рис. 5.2).
Обсуждая вопрос о поведении системы при больших квантовых числах, мы показали, что при этих условиях поведение частицы утрачивает особенности, характерные для микромира — оно скорее напоминает ее классическоеповедение. Это является частным случаем более общего принципа — принципа соответствия, выдвинутого Бором, который гласит:
любая новая теория, претендующая на большую общность, чем общепринятые теории, обязательно должна переходить в «старую» в тех условиях, в которых была построена и проверена на опыте «старая физика».
Date: 2015-05-19; view: 987; Нарушение авторских прав