Спин фотона

Обсудим теперь более подробно вопрос об излучении, возникающем при

переходах атома из возбужденного состояния в основное либо в одно из нижележащих возбужденных состояний. Для этого необходимо прежде всего разобрать вопрос о собственном моменте импульса фотона, т. е. его спине.

Из оптики известно, что световые волны являются поперечными и могут иметь различную поляризацию. В качестве основных поляризационных состояний обычно рассматривают две взаимно перпендикулярные линейные поляризации. В квантовой механике за исходные поляризации удобнее выбирать не линейные, а циркулярные, т. е. соответствующие вращению векторов электрического и магнитного полей световой волны по или против часовой стрелки. Вектор момента импульса электромагнитного излучения

направлен при этом по направлению (у правовращающегося) или против направления (у левовращающегося) движения фотона. Переходя на язык квантовой механики, мы должны сказать, что у фотона есть спин, причем проекция спина на направление движения может принимать два значения —плюс или минус единицу. Существование только двух возможных проекций спина, казалось бы, означает, что он равен 1/2, поскольку такое значение спина обеспечивает, согласно правилам квантования, необходимое число

проекций на заданную ось 2s + 1 = 2. Однако подобное заключение полностью противоречит опыту, ибо в таком случае фотоны были бы фермионами.

Тогда, в частности, при испускании фотона атомом полный угловой момент последнего мог бы меняться на 1/2, чего никогда не наблюдается. Кроме того, при этом фотон подчинялся бы принципу запрета Паули и никаких электромагнитных волн быть не могло — в таком случае максимальная передаваемая передатчиком энергия была бы равна ћω. Следовательно, спин фотона должен выражаться целым числом.

Указанные необычные свойства фотона обусловлены равенством нулю его массы. Отличие безмассовой частицы от массовой заключается в том, что для первой невозможно найти такую систему отсчета, в которой она покоится, поскольку она движется со скоростью света, т. е. нельзя определить спин как момент импульса частицы в системе отсчета, где она покоится.

Подчеркнем, что отличие между системой отсчета и системой координат состоит в следующем: система отсчета всегда связана с материальными телами, тогда как система координат представляет собой математический образ, не связаный с какими-либо материальными телами. Поэтому у безмассовой частицы всегда есть только одно выделенное направление — направление ее скорости (волнового вектора).

Таким образом, для безмассовой частицы можно говорить лишь об акаксиальной симметрии относительно этого выделенного направления; иными словами, для фотона пространство обладает аксиальной симметрией. Выражение такой симметрии — сохранение проекции момента на направление импульса, которая может быть равна только ±1. Такие значения проекции момента импульса фотона на направление импульса соответствуют правовращательной и левовращательной круговой поляризацией. Значение «0» исключается поперечностью электромагнитных волн, так как нулевое значение проекции момента импульса фотона на направление его движения соответствовало бы

продольной поляризации световой волны.

Отсюда следует достаточно сильное утверждение: понятие о спине фотона условно (для фотона нельзя последовательно различать спин и орбитальный момент как составные части его полного момента), и смысл имеет лишь полный момент импульса j = 1, 2, 3,... (нуль невозможен).

Прежде, чем перейти к описанию различных состояний фотона, кратко остановимся на вопросе о четности состояния. Понятие «четность состояния» связано с операцией изменения направления осей координат на обратное (так называемая пространственная инверсия). Обозначим соответствующий оператор Р. Его действие на волновую функцию состоит в замене х —> -х, у —> -у, z --> -z. Чтобы выяснить, каким может быть результат

действия оператора Р на некоторую волновую функцию ψ, подействуем им на ψ дважды. Тогда, по определению операции инверсии, мы должны получить ту же самую функцию (двукратное отражение осей координат ничего не меняет), т. е. Р²ψ = ψ. Отсюда следует, что собственными значениями оператора Р являются ±1: Рψ = ±ψ. В соответствии с этим в квантовой механике различают четные и нечетные состояния (или состояния положительной и отрицательной четности). Так например, четность состояния атома водорода равна (-1)^l, т. е. s- и d-состояния являются четными, а р- и f-состояния — нечетными.

Процесс испускания или поглощения фотонов атомами должен присходить с соблюдением законов сохранения энергии, импульса и четности системы.

Теперь вернемся к состояниям фотона. Для обозначения различных состояний с определенными моментами и четностями принята следующая терминология: фотон с моментом j и четностью, равной (-1)^j, называют 2^j-польным электрическим фотоном (или E-фотоном); если же у фотона с моментом j четность равна (-1)^j+1, то его называют 2^j-польным магнитным фотоном (или М-фотоном).

Иначе говоря, если обозначать состояние фотона с моментом j и четностью π как j^j, то

фотоны электрического типа — это фотоны типа 1^-, 2+, 3^-, 4+,...; магнитного типа — это фотоны типа1⁺, 2^-,3⁺,4",...

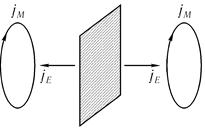
Рис. 8.1

Названия «электрического» и «магнитного» типа произошли оттого, что вектор тока является нечетной пространственной функцией (он при отражении в зеркале меняет свое направление), а круговой ток (магнитный диполь) направление своего вращения при отражении в зеркале не меняет (рис. 8.1).

Возможна иная интерпретация квантового числа j: оно указывает тип симметрии, которым данное состояние обладает относительно вращения, т. е. образно говоря, дает изображение атома с разных сторон:

j = 0 — сферическая симметрия,

j = 1 — свойство симметрии вектора (диполя),

j = 2 — пространственная симметрия квадруполя,

j = 3 — пространственная симметрия октуполя и т. д.

Поэтому к слову «фотон» обычно добавляют «дипольный», «квадрупольный», «октупольный» и т. д. Поскольку структуру Е0-мультиполя (сферическая симметрия) имеет кулоновское поле точечного заряда, действие лоновского поля иногда трактуют как результат обмена промежуточным виртуальным Е0-фотоном. Таким образом на самом деле спин фотона (вернее, его момент импульса) может быть любым, а не только равным 1.

Если размер излучающей системы равен а, а ω — частота излучения, то электрическое поле квадруполя меньше поля диполя в аω/с раз (с — скорость света). Этот множитель можно представить в виде:

аω/с = (2πν/с) а = 2πа/λ. (8.1)

Поскольку мы рассматриваем излучение атомов, то в данном случае а — размер атома, λ — длина волны излучения. Мощность излучения пропорциональна квадрату электромагнитного поля, а следовательно, «скорость» потери энергии возбужденным атомом при дипольном излучении в (2πа/λ)² раз больше, чем при квадрупольном, и соответственно, относительная продолжительность излучения, называемая временем эюизни атома в возбужденном состоянии, будет обратно пропорциональна этой величине.

При излучении в видимом оптическом диапазоне длин волн справедлива следующая оценка:

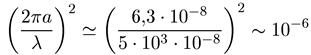
Если обозначить время жизни атома в возбужденном состоянии через т, а

обратную ему величину — вероятность перехода атома из возбужденного

состояния — через w, то мы в результате получим

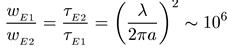
Аналогичное соотношение имеет место между магнитным и электрическим переходами одинаковой мультипольности

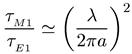(8.4)

Оно легко обобщается на переходы с любой мультипольностью.

Соотношения (8.3) и (8.4) означают, что практически в атомах происходят лишь электрические дипольные переходы, т. е. переходы с испусканием дипольных El-фотонов (вернее, если возбужденное состояние может «высветиться» через различные переходы, среди которых есть и Е1, то именно он будет преобладающим). Поэтому часто говорят, что спин фотона равен единице, хотя — подчеркнем еще раз — спин фотона (вернее его полный момент импульса) может быть любым. В квантовой системе гораздо меньшего

размера — в ядре — мы довольно часто наблюдаем испускание квадрупольных квантов.

Date: 2015-05-19; view: 4581; Нарушение авторских прав