Квантовый осциллятор

Перейдем теперь к рассмотрению характерных задач квантовой механики, и прежде всего к задаче о квантовом осцилляторе. Общее для всех осцилляторов заключается в том, что их энергия складывается из двух частей. Одно слагаемое пропорционально квадрату отклонения осциллятора от положения равновесия — это потенциальная энергия. Если q — величина такого отклонения, то потенциальная энергия равна

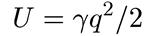(5.20)

Коэффициент 7 называется «жесткостью» осциллятора. Второе слагаемое — кинетическая энергия — может быть записано в виде

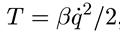
Т = βq′²/2, (5.21)

где q′ — скорость изменения величины q во времени. Величину β называют «массой осциллятора». Как бы ни был конкретно устроен осциллятор, его угловая частота ω = 2πv и период колебаний Т выражаются через жесткость γ и массу β следующим образом:

ω = √(γ/β)

T = 2π√(γ/β)

случае маятника можно считать, что роль жесткости играет ускорение силы тяжести g, а массы — длина маятника l (поскольку для маятника как кинетическая, так и потенциальная энергия — обе пропорциональны реальной механической массе). Таким образом можно рассмотреть сразу все осцилляторы независимо g от их физической природы. Иначе говоря, осциллятором является частица, движущаяся в потенциале

вида

U = (1/2)mω²x² (5.23)

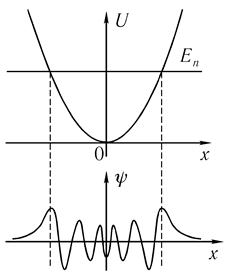
Рис. 5.4

где ω — частота классического осциллятора (на рис. 5.4 изображен потенциал гармонического осциллятора и дано схематичное изображение волновой функции стационарного состояния). В общем случае это задача о малых колебаниях вблизи положения устойчивого равновесия. Нам несущественно, как реализован осциллятор: представляет ли он собой груз на пружинке или колебательный контур.

Согласно осцилляционной теореме, если частица движется в области размером L, то на этой длине должно укладываться целое число полуволн (т. е. должна образоваться стоячая волна):

L(E_n) ~ nλ/2 (5.24)

Поскольку длина волны де Бройля

λ = h/√(2mE), (5.25)

то, если энергию отсчитывать от дна ямы, получаем

L_n = L(E_n) ~ πћn/√(2mE_n). (5.26)

Найдем, как зависит в нашем конкретном гармоническом потенциале характерный размер L от энергии уровня Еn. Характерная область находится из условия

U(L) = Е_n. (5.27)

Из выражения для потенциала (5.23) получаем

Е_n~ (1/2) mω²L²_n —> L_n ~ √E_n/ω. (5.28)

С учетом (5.26) находим следующее соотношение

√E_n/ω ~ πћn/√(2mE_n)

(5.29)

или

Е_n= Сnћω, (5.30)

где С — константа. Чтобы отыскать ее величину, воспользуемся принципом соответствия Бора, который в нашем случае означает, что при больших квантовых числах расстояние между соседними уровнями должно равняться классической частоте движения, т. е.

dE_n/dn = ћω_кл. (5.31)

Отсюда сразу следует, что С = 1.

Точное решение задачи о гармоническом осцилляторе приводит к спектру

его состояний

Е_n= (n + l/2)ћω. (5.32)

Таким образом, при n = 0 энергия равна не нулю, a E₀ = ћω/2. Это связано

с соотношением неопределенностей, и, как мы уже неоднократно подчеркивали, используя его, легко получить оценку нулевой энергии. Учитывая, что

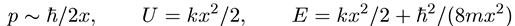
р ~ ћ/2x, U = kх²/2, Е = kх²/2 + ћ²/(8mх²) (5.33)

и минимизируя полную энергию, находим характерную амплитуду нулевых

колебаний осциллятора

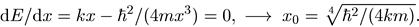
dE/dx = kх- ћ²/(4mх³) =0, —> х₀ = ⁴√(ћ²/(4km)). (5.34)

Подставляя (5.34) в выражение для энергии (5.33), получаем

Е₀ = ћω/2. (5.35)

Отметим, что спектр оказался эквидистантным. Кроме того, легко записать уравнение квантования энергии трехмерного осциллятора как сумму трех одномерных:

Е_n = ћω(n₁ + n₂ + n₃ + 3/2) = ћω (n + 3/2), (5.36)

где n = n₁ + n₂ + n₃ называют главным квантовым числом осциллятора.

Мы применили к осциллятору, не интересуясь его устройством, принципы квантовой механики, установленные первоначально для некой частицы, находящейся в потенциальной яме (электрона). Естественно ожидать, что общие принципы должны быть такими же и для других частиц.

Особо следует подчеркнуть одно важное свойство квантового осциллятора. Когда энергия минимальна, классический осциллятор находится в покое в положении равновесия, между тем как квантовый в наинизшем состоянии при n = 0 совершает колебания — «нулевые колебания». Кинетическая и потенциальная энергии этих колебаний ~ ћω. Среднее значение координаты осциллятора равно нулю, а среднее значение квадрата координаты дается приведенной выше формулой. Это замечательное свойство квантовых осцилляторов хорошо проверено на опыте и чрезвычайно важно для современной физики.

Если мы рассмотрим звуковые колебания твердого тела как набор квантовых сцилляторов, то получим, что при абсолютном нуле температуры все атомы твердого тела не неподвижны, а совершают нулевые колебания.

Это подтвердили опыты по рассеянию света при низких температурах. Если же рассмотривать электромагнитные волны как набор осцилляторов в пустом пространстве, то мы придем к заключению, что в пустоте, даже когда в ней нет частиц или квантов, должны происходить «нулевые колебания» электромагнитного поля, и эти колебания также были обнаружены.

Date: 2015-05-19; view: 1005; Нарушение авторских прав