Принцип Паули

Химикам давно было известно, что свойства многих элементов подобны.

Например, Не, Ne, Ar, Kr, Xe представляют собой благородные газы и весьма «неохотно» участвуют в химических реакциях, a Li, Na, К, Rb, Cs являются щелочными металлами с одной валентностью. Сходными свойствами обладают галогены F, C1, Вг, I. Число подобных примеров можно увеличить. Немногим более ста лет назад, в 1869 г, Д.И. Менделеев обнаружил, что отмеченное подобие не случайно, а связано с определенной периодичностью в свойствах химических элементов. По мере увеличения атомного веса такие свойства меняются «циклически» — через некоторое время они повторяются.

К своим результатам Менделеев пришел чисто эмпирически на основе изучения большого экспериментального материала, но вопрос о том, чем обусловлена найденная закономерность, оставался открытым. Как уже указывалось, первый шаг в этом направлении был сделан в лаборатории Резерфорда во втором десятилетии XX в. Было выяснено, что периодичность элементов связана не с их атомным весом, как думал Менделеев, а с величиной заряда ядра, равная числу атомных электронов. Менделеев был прав постольку, поскольку атомный вес стабильных изотопов для каждого химического элемента монотонно возрастает с увеличением заряда ядра и числа электронов. Поэтому почти безразлично, как располагать элементы — по числу электронов или по атомному весу.

Следующим этапом явилась работа Н. Бора, опубликованная в 1923 г. Бор полагал, что электроны в атоме обращаются вокруг центрального ядра по замкнутым орбитам. Форма каждой орбиты и ее удаление от ядра характеризуются орбитальным квантовым числом /, определяющим угловой момент электрона и главным квантовым числом п. Химические свойства атома в основном зависят лишь от распределения электронов на орбитах с наибольшим значением главного квантового числа п. Такие электроны более других

удалены от ядра и потому связаны с ним менее прочно, они гораздо легче отвечают на внешние возмущения, чем электроны на «внутренних» орбитах.

Периодичность, открытая Менделеевым, связана с тем, что определенная совокупность электронных орбит образует «замкнутую оболочку», представляющую собой сферически симметричное и весьма устойчивое в химическом плане образование. Атомы с целиком заполненными оболочками — инертные газы — очень слабо реагируют на внешние возмущения, поскольку их потенциал ионизации существенно больше, чем у остальных элементов.

В других атомах эти заполненные оболочки эффективно уменьшают, как говорят, экранируют, положительный заряд центрального ядра. В химических реакциях участвуют только электроны, находящиеся на еще незаполненной оболочке. Свойства атомов с одинаковым числом таких электронов оказываются подобными. Так, например, все атомы с одним электроном сверх заполненной оболочки — щелочные металлы — одновалентны. Атомы с двумя «лишними» электронами — щелочноземельные металлы Be, Mg, Ca, Sr,

Ва — двухвалентны и т. д.

Из таблицы Менделеева видно, что в атомах благородных газов Не, Ne, Ar, Кг, Хе, Rn имеется соответственно 2, 10, 18, 36, 54, 86 электронов. Каждый такой атом отличается от предыдущего заполнением новой оболочки. Отсюда легко найти количество электронов в замкнутых оболочках: оно равно разностям чисел электронов в соседних инертных газах, т. е. 2, 8, 8, 18, 18, 32. Ридберг заметил, что этот ряд чисел описывается простой формулой

2N², где N — целое число, равное по очереди 1, 2, 3, 4. Такая закономерность, как мы убедимся, является весьма знаменательной. Что же касается повторяющихся в этой последовательности чисел 8 и 18, то это связано, как мы увидим в дальнейшем, с порядком заполнения состояний в атомах.

В развитом Бором представлении об оболочечном строении атома было одно нечеткое место. Надо было делать специальное предположение, — на низших орбитах атома может находиться лишь ограниченное число электронов.

Такое положение существовало до тех пор, пока в январе 1925 г. В. Паули не сформулировал принцип запрета, носящий его имя. В нашем конкретном случае он означает, что в атоме не может существовать двух или больше эквивалентных электронов, т. е. электронов, для которых значения всех квантовых чисел одинаковы. Если в атоме находится электрон в состоянии, характеризуемом некоторым набором значений квантовых чисел, то это состояние «занято».

В квантовой механике одинаковые частицы рассматриваются полностью тождественными. Что это означает? В классической механике мы можем пометить частицы. Например, при упругом ударе одного биллиардного шара по другому можно указать, какой из шаров после соударения покатился вправо, а какой влево. В квантовой механике это в принципе невозможно из- за отсутствия траекторий у частиц и перекрытия их волновых функций в области, где происходит столкновение. Одинаковые частицы теряют свою индивидуальность, что отражается введением так называемого принципа

тождественности частиц, согласно которому все частицы одного сорта абсолютно неразличимы; возможность «пометить» их означала бы сделать их разными, что невозможно.

Принцип тождественности частиц на языке волновых функций, описывающих в квантовой механике их поведение, означает, что волновые функции системы частиц, получающиеся друг из друга перестановкой пар одинаковых частиц, могут отличаться только несущественным множителем

е^if,

где f — вещественное число. Добавление этого множителя не меняет ни плотности вероятности |ψ|² обнаружения частиц, ни средних значений физических величин. Если сделать перестановку частицы еще раз, то получится функция, отличающаяся от исходной множителем е^2if. Так как при этом система

возвращается в исходное состояние, то

е^2if = 1 и

е^if = +-1.

Следовательно,

перестановка пары частиц местами либо оставляет волновую функцию неизменной, либо меняет ее знак. И поскольку состояние частицы характеризуется как ее положением в координатном пространстве, так и ориентацией ее спина, то в первом случае волновая функция является симметричной функцией координат и проекций спинов частиц, а во втором —антисимметричной.

Как показывает опыт, симметрия или антисимметрия волновой функции зависит от спина частиц. Частицы с полуцелым спином, в том числе электроны, протоны, нейтроны, описываются только антисимметричными волновыми функциями, они подчиняются статистике Ферми-Дирака и потому называются фермионами. Частицы с целым спином — фотоны, мезоны и др. — описываются только симметричными волновыми функциями, они подчиняются статистике Бозе-Эйнштейна и называются бозонами. Как показал Паули, этот опытный факт может быть обоснован в рамках квантовой теории поля.

Антисимметрия волновых функций одинаковых частиц с полуцелым спином — фермионов — приводит к особенно простым и наглядным следствиям в приближении невзаимодействующих частиц. Если пренебречь их взаимодействием друг с другом, то каждую частицу системы можно считать находящейся в определенном состоянии и волновую функцию всей системы представить в виде произведения волновых функций отдельных частиц, а полную энергию Е системы полагать равной сумме энергий частиц системы.

Рассмотрим для простоты систему из двух частиц. В этом случае энергия

системы

Е = Е₁ + Е₂,

где Е₁ — энергия первой частицы в состоянии, описываемом волновой функцией

ψ_α(r₁,s_z1), a

E2 — энергия второй частицы в состоянии

ψ_β(r₂,s_z2).

Здесь r₁, г₂ — координаты первой и второй частиц, а

Ss_z1 и s_z2

— проекции их спинов на ось z. Решением уравнения Шредингера

для такой системы будет произведение

ψ₁ = ψ_α(r₁,s_z1) ψ_β(r₂,s_z2), (7.1)

а если под цифрами 1 и 2 понимать совокупность всех переменных, от которых зависят волновые функции первой и второй частиц, то можно переписать его в виде

ψ₁(1,2) = ψ_α(1) ψ_β(2). (7.2)

Такая запись волновой функции системы страдает тем недостатком, что мы, как это было в классике, «пометили» частицы, т. е. указали, какая их них номер 1, а какая номер 2. Ясно, что в случае одинаковых частиц решение уравнения Шредингера с той же энергией Е может также иметь вид

ψ₁₁(1,2) = ψ_α(1) ψ_β(2). (7.3)

Теперь вторая частица находится в состоянии ψ_α с энергией Е₁, а первая — в

состоянии ψ_β с энергией Е₂. Таким образом, имеется двукратное вырождение, связанное с симметрией задачи по отношению к перестановке частиц местами.

Рассмотрим, как правильно записать волновую функцию всей системы.

Если система может находиться в двух разных состояниях, имеющих одну

и ту же энергию и описываемых волновыми функциями ψ₁ и ψ₂, то согласно

принципу суперпозиции, любая их линейная комбинация

ψ = c₁ψ₁ + с₂ψ₂ (7.4)

(где c₁, с₂ — произвольные числа) будет также решением уравнения Шредингера. Поскольку волновая функция системы должна быть либо симметричной, либо антисимметричной, то или с₁ = c₂ или с₁ = - c₂. Нормированная на единицу симметричная функция при α /= β имеет вид

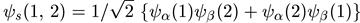, (7.5)

а антисимметричная функция

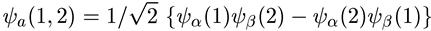(7.6)

1/√2 — нормировочный множитель). Полученные формулы легко обобщить на случай систем из любого числа частиц.

Из формулы G.6), описывающей волновую функцию системы невзаимодействующих фермионов, следует крайне интересный и принципиальный для их поведения результат. Если бы две частицы оказались в одном и том же состоянии (ψ_α = ψ_β, т. е. частицы находятся в одном и том же месте пространства и в одном и том же спиновом состоянии), то волновая функция (7.6) обратилась бы в нуль. Это означает, что в системе одинаковых частиц с полуцелым спином две (или более) частицы не могут одновременно находиться в одном и том же состоянии. Последнее утверждение и называется принципом исключения (запрета) Паули или просто — принципом Паули. В общем случае для систем одинаковых взаимодействующих частиц с полуцелым спином принципом Паули часто называют требование антисимметрии волновых функций.

Принцип запрета Паули делает понятной оболочечную структуру атома.

Если все состояния на низших орбитах уже заполнены электронами, то новой частице не остается ничего другого, как занять свободное место на более высокой орбите. Более того, этот принцип позволяет понять правило Ридберга для числа электронов в заполненной оболочке атома. При заданном значении главного квантового числа п полное количество всех допустимых значений орбитального числа l и магнитного квантового числа m_l равно n².

Каждое состояние электрона в атоме, однако, характеризуется не только величинами n, l, m_l, но и значением четвертого квантового числа — спинового, которое обозначается m_s. Последнее двузначно: оно принимает значения m_s = 1/2 либо m_s = -1/2. Поэтому полное число состояний электрона при заданном числе п и произвольных l, m_l m_s равно 2n². Полученный результат в точности совпадает с выражением Ридберга для числа электронов в заполненной атомной оболочке, если положить N = n.

Таблица Менделеева

В настоящем параграфе мы кратко рассмотрим, как описываются состояния сложных атомов. Для этого нам понадобится правило сложения моментов, о котором шла речь раньше.

Чтобы описать структуру сложного атома, надо знать состояния всех его электронов. Опыт показывает, что в легких и средних атомах орбитальные моменты отдельных электронов складываются в суммарный орбитальный момент

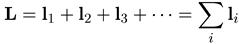, (7.7)

а спиновые — в спиновый:

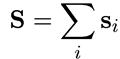, (7.8)

и полный момент равен

J = L + S. (7.9)

В этих случаях говорят, что имеет место LS-связъ или рассел-саундеровская связь. В тяжелых атомах осуществляется так называемая jj-связь, когда полный момент равен сумме полных моментов отдельных электронов, т. е.

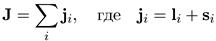, (7.10)

Константами движения являются не только полный момент J, но и абсолютные значения L и S и их проекции на вектор J.

Состояния атомов обозначаются аналогично тому, как это делается для отдельных электронов, но только большими буквами: состояния с L = 0, 1, 2, 3,... обозначаются соответственно буквами S, P, D, F,... Справа внизу указывается значение квантового числа J, а слева вверху — величина 2S +1; если S < L, то эта величина определяет мультиплетность состояния, т. е. число состояний с одинаковыми L и S, но разными J. Например, если атом углерода находится в состоянии ³P₀, то это означает, что L = 1, S=1,

J = 0.

Состояние отдельного электрона в атоме определяется квантовыми числами n, l, m_l, m_s. Зададим некоторое орбитальное число l и рассмотрим, скольким состояниям оно соответствует. При заданном l возможно 2l +1 разных значений m_l, но каждому m_l соответствуют два состояния с m_s = ±1/2, т. е. всего 2(2l + 1) состояний с разными m_l и m_s. Таким образом, при любом значении квантового числа n в атоме может быть в

s-состоянии — 2 электрона,

p-состоянии — 6 электронов,

d-состоянии — 10 электронов и т. д.

Говорят, что совокупность электронов, имеющих одинаковые n и l, образует оболочку атома. Согласно этой терминологии говорят об s-оболочках атомов, p-оболочках и т. д. Термин «оболочка» применяется также в смысле совокупности всех электронов, окружающих атомное ядро. Разумеется, при данном п значения квантового числа / не могут превышать n - 1 (см. гл. 4).

Всего в этом случае может быть 2n² состояний, т. к. n = n_r+l, 0 < l< n - 1, и

все эти состояния образуют электронную оболочку атома с главным квантовым числом п. Оболочки, как и электронное состояние атома, обозначаются большими латинскими буквами:

n = 1 К-слой l = 0 (s-оболочка),

n= 2 L-слой l = 0, 1 (s-, или p - оболочка),

n = 3 М-слой l = 0, 1, 2, (s-, p-, d-оболочка) и т. д.

Рассмотрим теперь, как последовательно заполняется таблица Менделеева. Созданная на чисто эмпирических правилах, исходя из химических свойств элементов и их подобия, периодичность свойств элементов нашла свое естественное обоснование лишь на основе квантовой механики. Впервые объяснение периодической таблицы Менделеева с точки зрения квантовой механики было дано Н. Бором.

В табл. 7.1 приведены квантовые характеристики атомов вплоть до аргона. Здесь использовано стандартное обозначение электронных конфигураций атомов: в скобках стоит спектроскопическое обозначение электронного уровня nl_j, а вверху — число электронов, находящихся на этом уровне.

Таблица 7.1. Электронные состояния легких атомов

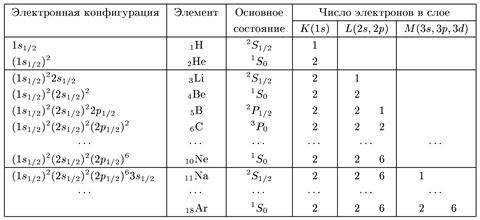
Таблица показывает, что до бора у всех элементов (Не, Li, Be) полностью заполнен К-слой, а у L-слоя заполнена 2s-оболочка. У более тяжелых элементов (от бора до неона) остовом служит электронная конфигурация (ls_1/2 )² (2s_1/2)². В боре начинается заполнение p-состояний, в которых проекция спина может быть ±1/2, а проекция орбитального момента m_l = 0, ±1.

Возникает естественный вопрос о том, с какими значениями m_l и m_s электроны будут последовательно заполнять р-оболочку? Здесь вступает в игру правило Хунда, согласно которому наименьшая энергия соответствует состоянию с максимальным суммарным значением S. При этом J = |L - S|,

если заполнено не более половины оболочки, и J = L + S в остальных случаях. Последнее иллюстрируется табл. 7.2.

Таблица 7.2. Квантовые характеристики электронов у атомов от бора до неона

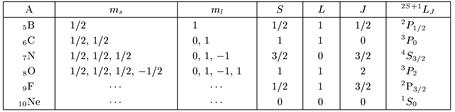
Теперь надо объяснить, почему в таблице Менделеева наблюдается периодичность химических свойств элементов и чем выделены благородные газы.

Благородными называются газы химически почти полностью инертные, их потенциал ионизации — энергия отрыва одного электрона — оказывается наибольшим, как это отчетливо видно из рис. 7.1.

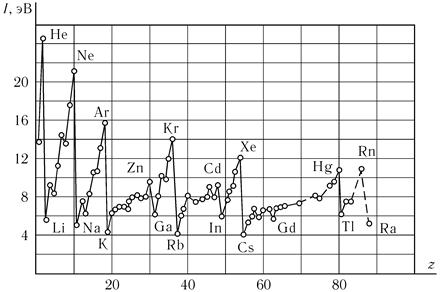
Pис. 7.1.

С квантовой точки зрения инертные газы — это элементы, у которых целиком заполнена р-оболочка; им соответствует состояние с S = 0, L = 0, J = 0.

Дело в том, что электроны s-оболочки расположены близко к ядру, они не являются внешними, а вот р-оболочка — внешняя и ее заполнение приводит к инертности элемента. При заполненной р-оболочки после неона электроны опять вначале заполняют 3s-состояние, от чего и возникает периодичность химических свойств.

Правда, с порядком заполнения электронных оболочек у более тяжелых атомов все обстоит далеко не так просто, поскольку с ростом числа электронов в атоме существенную роль начинает играть экранирование поля ядра внутренними электронами, и электрическое поле, в котором находятся внешние электроны, заметно отличается от кулоновского. В результате порядок заполнения (от s-k p-, a затем к d- и f-оболочкам) начинает нарушаться уже после Аr. Экранирование приводит к тому, что в d- и f-состояниях электроны находятся эффективно ближе к ядру, чем в s- и p-состояниях.

Поэтому именно s- и p-электроны (а не d- и f-электроны) определяют химические свойства элемента. Например, заполнение 4f-состояний у редкоземельных элементов практически не меняет их химических свойств. А что касается g-состояний (l = 4), которые должны были появляться в оболочке с главным квантовым числом n = 5, то из-за упомянутого эффекта экранирования их заполнение становится энергетически невыгодным, и в реально существующих атомах они вообще не заполняются.

Атомные номера инертных элементов иногда называют магическими числами, поскольку на первый взгляд кажется, что в их последовательности не наблюдается никакой закономерности. Однако они простое следствие товомеханических закономерностей заполнения электронных состояний.

Действительно, инертными являются элементы с порядковыми номерами

2, 10, 18, 36, 54, 86,... У гелия два электрона в ls-состоянии полностью

заполняют K-слой, у неона добавлются еще 2 электрона в 2s-состоянии и 6

в 2р — итого 10 электронов, у аргона — еще 8 электронов в состояниях 3s,

3р и т. д., таким образом магические числа соответствуют, как указывалось

выше, заполнению очередной р-оболочки — 2p, 3р, 4p, 5р.

ГЛАВА 8

Date: 2015-05-19; view: 1269; Нарушение авторских прав