Атом водорода в квантовой механике. Атом водорода состоит из массивного положительно заряженного ядра и движущегося вокруг него легкого отрицательно заряженного электрона

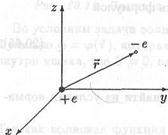
Атом водорода состоит из "массивного" положительно заряженного ядра и движущегося вокруг него "легкого" отрицательно заряженного электрона (рис. 21.1). Электрон - это микроскопическая частица, "усле­дить" за движением которой не представляется возможным. Другими словами, нельзя описать движение электрона посредством зависимости его радиус-вектора от времени. В квантовой механике движение частицы описывают при помощи волновой функции, которая определяет вероят­ность обнаружить частицу в том или ином месте пространства.

Если частица движется в пространстве, то описывающая ее движение
волновая функция будет зависеть в общем случае от времени и коорди­нат:

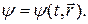
Рис. 21.1.Электрон в атоме водорода

Эту функцию можно найти из уравнения Шредингера

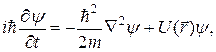(21,0

где

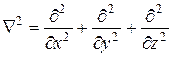
оператор Лапласа, 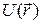– потенциальная энергия частицы.

Ядром в атоме водорода является протон, заряд которого равен +е. Так как заряд электрона равен - е, потенциальная энергия электрона в атоме водорода выражается формулой

= -

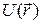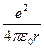
где расстояние от ядра до электрона

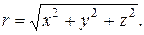(21.2)

По определению волновая функция, описывающая стационарное со­стояние электрона, имеет вид

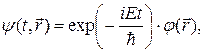(21.3)

где функция 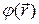есть решение стационарного уравнения Шредингера

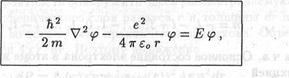
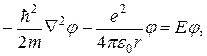(21.4)

где Е - энергия электрона в стационарном состоянии.

В сферической системе координат уравнение Шредингера для атома водорода

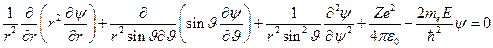
Это уравнение решается методом разделения переменных.

Функции, являющиеся решениями этого уравнения образуют счетное множество. Каждой из них присваивается трехзначный номер nlm:

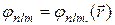
Число п принимает значения 1, 2, 3,... и называется главным квантовым числом.

Для заданного значения п число l, называемое орбитальным, принимает одно из п значений 0, 1, 2,..., п- 1.

Наконец, магнитное квантовое число т принимает значения - l, - l +1,..., - 1, 0, 1, 2,..., l - 1, l. Всего при заданном значении l число т принимает 2 l + 1 значение.

Квантовые числа п, l и m имеют следующий физический смысл.

Глав­ное квантовое число п определяет возможные значения энергии электро­на в атоме водорода:

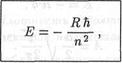
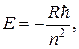
где n = 1, 2, 3,…

п = 1. 2, 3,...

■

Орбитальное квантовое число l дает возможность вычислить модуль L вектора 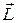момента импульса электрона: (21.5)

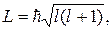l = 0, 1, 2, …, n – 1.

Проекция вектора L момента импульса электрона на заданное напра­вление z в пространстве определяется формулой

L _z = ħm, (21.8)

где магнитное квантовое число т принимает значения:

m = - l, - l + 1, …, -1, 0, 1,…, l – 1, l.

Задача. Основное состояние электрона в атоме водорода описыва­ется функцией

φ (r) = A exp (- α r), (21-9)

где А и α - постоянные величины. При помощи уравнения (21.4) найти постоянную а и энергию частицы Е в этом состоянии. Найти постоянную А из условия нормировки.

Ответы:

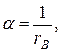(21.10)

первый боровский радиус,

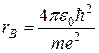
E = - Rħ,

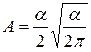. (21.11)

Про функции 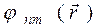говорят, что они описывают "электронные обла­ка". Точнее говоря, они определяют распределение в пространстве плот­ности вероятности:

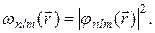
Электронное облако - это часть пространства, где плотность вероятно­сти w_nlm принимает наибольшие значения. Поэтому вероятность обнару­жить электрон в этой части пространства, т.е. внутри облака, почти рав­на единице; а вероятность обнаружить его вне облака практически равна нулю. Электронные облака в атоме имеют сложную форму и окружают ЯДРО СЛОЯМИ.

При l = 0 (в этом случае число m также равно нулю) электронное облако имеет сферически симметричную форму, т.е. плотность вероят­ности u;_noo является сферически симметричной функцией

ω_{n 00}(r) = | φ_{n 00}(r)|²,

зависящей только от расстояния г от электрона до ядра. По определе­нию произведение плотности вероятности на объем некоторой части про­странства есть вероятность обнаружить здесь рассматриваемую частицу. Внутри тонкого сферического слоя радиуса r и толщины dr плотность вероятности w_noo во всех точках практически одинакова. Объем сфери­ческого слоя равен 4 π r ² dr.²dr. Поэтому выражение

dP = f_n (r) dr = | φ_{n 00}(r)|² 4 π r ² dr

есть вероятность того, что расстояние от электрона до ядра принимает значение из интервала (r, r + dr).

f_n (r)

■

r _B 4 r _B r

Рис. 21.2. Плотность вероятности f_n (r) обнаружить электрон на расстоянии r от ядра

Задача. Электронное облако, которое представляет электрон, нахо­дящийся в основном состоянии в атоме водорода, описывается функцией

f ₁ (r) = | φ₁₀₀(r)|² 4 π r ², (21.12)

где φ ₁₀₀ (r)есть функция (21.9). Значение r_вер расстояния г, при кото­ром функция f_n (r) достигает наибольшего значения, называется наибо­лее вероятным расстоянием от электрона до ядра. Доказать, что для электрона в основном состоянии наиболее вероятное расстояние до ядра равно радиусу первой боровской орбиты: r_вер = r_B.. Графики функции

f_n (r) = | φ_{n 00}(r)|² 4 π r ²

при п =1 и 2 показаны на рис. 21.2. Функция fi(r) принимает Наи­
большее значение при r = r_в, а функция f ₂(r)-при r= 4 r _B. Можно
показать, что наиболее вероятное расстояние от электрона, находящего­
ся в стационарном состоянии φ_n00 до ядра равно радиусу n-ой боровскрй
орбиты:

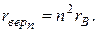
Так как энергия электрона в атоме водорода зависит только от глав­ного квантового числа п, каждому значению энергии Е_п соответствует несколько различных состояний. Такие состояния называются "выро­жденными", а их число g_п называется кратностью вырождения данного энергетического уровня.

Date: 2015-05-19; view: 768; Нарушение авторских прав