Гиромагнитное отношение

Представим себе, что электрон в атоме движется со скоростью v по круговой орбите радиуса г (рис. 21.4).

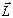
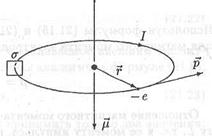
Рис. 21.4. Момент импульса и магнитный момент электрона

Как любая движущаяся частица, электрон обладает моментом им­пульса , который равен векторному произведению радиус-вектора 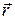на импульс :

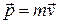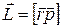. (21.13)

Вектор L перпендикулярен плоскости, в которой лежит орбита электро­на, а, его модуль

L = mvr. (21.14)

Период обращения электрона вокруг ядра, т.е. время за которое он совершает один оборот, равен отношению пройденного за это время пути 2 πr к скорости электрона:

T = (21.15)

Двигаясь по орбите вокруг ядра, электрон один раз за период обраще­ния пересекает площадку σ, расположенную поперек траектории в некоторой ее точке (рис. 21.4). При этом через площадку переносится заряд е. Следовательно, движущийся по орбите электрон есть электрический ток, сила которого

I = 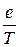(21.16).

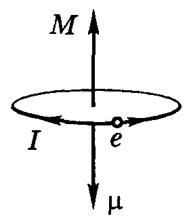
Так как заряд электрона отрицателен, направление этого тока противо­положно направлению движения электрона. Электрический ток, теку­щий в замкнутом контуре, характеризуется магнитным моментом 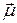. Это есть вектор, перпендикулярный плоскости контура. Направление векто­ра 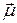связано с направлением тока правилом правого винта (рис. 21.4). Модуль магнитного момента равен произведению силы тока на площадь контура S:

μ = I S (21.17)

Для кругового тока площадь контура

S = π r ²

Используя формулы (21.15) и (21.16), получим следующее выражение для магнитного момента электрона:

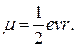
Отношение магнитного момента μ частицы к ее механическому момен­ту L, т.е. к ее моменту импульса, называют гиромагнитным отношени­ем. Для электрона на орбите это отношение равно

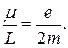
Более строгие расчеты приводят к этому же выражению.

Так как векторы 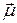и 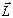антипараллельны, справедливо равенство

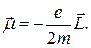(21.20)

Date: 2015-05-19; view: 805; Нарушение авторских прав