Спин электрона

Экспериментально и теоретически установлено, что электрон, являясь элементарной(т.е. неделимой) частицей, в то же время обладает внутренней структурой.это проявляется в том, что он может находиться в различных внутренних состояниях. Таких состояний всего два. До тех пор, пока отсутствуют какие –либо внешние воздействия на электрон.

Обнаружить, в каком именно из этих двух состояний находится электрон, невозможно.

Для объяснения экспериментальных фактов предполагают, что электрон обладает собственным моментом импульса, который обозначают 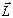_s и называют спином (от англ. spin - верчение, кружение). Модуль L_s это­го вектора можно вычислить по формуле

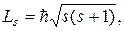(21.21)

которая аналогична формуле (21.7) для орбитального момента импульса. В формуле (21.22) квантовое число s принимает только одно значение:

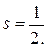
Таким образом, модуль спина электрона

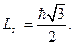(21.22)

Проекция L_Sz спина на направление z, задаваемое внешним магнит­ным полем, определяется формулой, которая аналогична формуле (21.8):

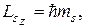(21.23)

Где спиновое квантовое число m_s может принимать только два значения

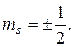
Именно число m_s служит характеристикой внутреннего состояния электрона. Электрон обладает также собственным магнитным моментом 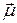_s, который связан с его спином соотношением

.

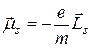При этом модули векторов 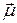_s и 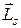соотносятся друг к другу как

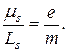
Это отношение называется спиновым гиромагнитным отношением. Как видно, оно в два раза больше орбитального гиромагнитного отношения(21.19)

Из формул (21.22), (21.23) и (21.24) найдем, что модуль 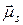, собственно­го магнитного момента jl_s электрона и его проекция μ_Sz на направление z определяются формулами

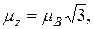
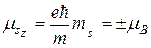(21.26)

где

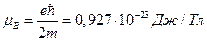
Величину μ_в называют магнетоном Бора.

Полный момент импульса электрона L_j равен векторной сумме орби­тального момента импульса 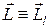и спина :

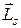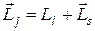(21.27)

Модули векторов 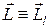и 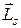определяются формулами

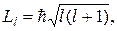
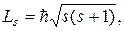
где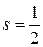

-где s = 1/2. Модуль вектора L_j определяется аналогичной формулой

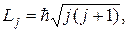
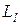
в которой квантовое число j может принимать значения:

j = l + s, | l – s |.

При l = 0 квантовое число j принимает только одно значение:

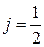
При l ≠ 0 число j может принимать значения:

.

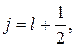
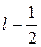Полный магнитный момент электрона 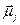равен сумме орбитального 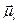и спинового 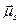, магнитных моментов:

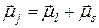(21.29)

В силу соотношений (21.20) и (21.24) вектор полного магнитного момента электрона не коллинеарен вектору полного механического момента L_j.

Date: 2015-05-19; view: 808; Нарушение авторских прав