
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Многоэлектронные атомы. Во всех атомах, кроме атома водорода, содержится более одного электрона
|
|
■
Во всех атомах, кроме атома водорода, содержится более одного электрона. В таких атомах каждый электрон взаимодействует не только с ядром, но и с другими электронами. При этом потенциальная энергия электрона будет равна сумме энергии его взаимодействия с ядром и энергий взаимодействия с остальными Z — 1 электронами:
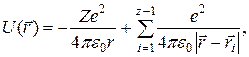
где 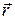 - радиус-вектор рассматриваемого электрона,
- радиус-вектор рассматриваемого электрона, 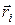 - радиус-вектор другого электрона, i = 1, 2,..., Z— 1. Так как электроны в атоме движутся с очень большими скоростями, можно считать, что каждый электрон движется в усредненном силовом поле, создаваемом другими электронами. Причем это силовое поле является сферически симметричным:
- радиус-вектор другого электрона, i = 1, 2,..., Z— 1. Так как электроны в атоме движутся с очень большими скоростями, можно считать, что каждый электрон движется в усредненном силовом поле, создаваемом другими электронами. Причем это силовое поле является сферически симметричным:
(21.30)
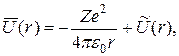
где 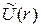 - усредненная потенциальная энергия взаимодействия одного электрона, находящегося на расстоянии r от ядра, со всеми другими электронами атома. Решения
- усредненная потенциальная энергия взаимодействия одного электрона, находящегося на расстоянии r от ядра, со всеми другими электронами атома. Решения
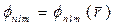 (21.28)
(21.28)
стационарного уравнения Шредингера
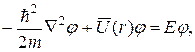 (21.31)
(21.31)
E = Enl
в котором потенциальная энергия электрона 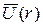 есть сферически симметричная функция от его координат, подобны волновым функциям
есть сферически симметричная функция от его координат, подобны волновым функциям 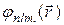 , описывающим стационарные состояния электрона в атоме водорода. Однако в данном случае энергия Е электрона, находящегося в стационарном состоянии, зависит не только от главного квантового числа п, но и от орбитального числа l:
, описывающим стационарные состояния электрона в атоме водорода. Однако в данном случае энергия Е электрона, находящегося в стационарном состоянии, зависит не только от главного квантового числа п, но и от орбитального числа l:
Е = Еп1.
Поэтому структуры энергетических спектров многоэлектронных атомов и спектров их излучения являются более сложными, чем у атома водорода.
Если не учитывать взаимодействие электронов, то энергию одного электрона в атоме приближенно можно положить равной его энергии в водородоподобном ионе:
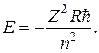 (21.32)
(21.32)
Состояние одного электрона в атоме характеризуется четверкой чисел п, l, т и ms. Состояния электрона с l = 0 называют s-состояниями, состояния с l = 1 - р-состояниями, состояния с l = 2 d-состояниями, состояния с l = 3 - f -состояниями и т.д. (табл. 1).
Таблица 1
| Число п | … | ||||
| Символ состояния электрона | s | р | d | f | … |
Значения главного квантового числа п указывают перед символом состояния. Таким образом, с учетом того, что для заданного п число l принимает значения 0, 1,..., п - 1, возможны следующие состояния электрона в атоме:
1s, 2s, 2р, 3s, Зр, 3d, 4s, 4p, 4d, 4 f,...
Например, символ Зр обозначает состояние с n = 3 и l = 1, т.е. состояние электрона, описываемое волновой функцией φ31т.
Совокупность электронных состояний  с одинаковыми п и l называется оболочкой, а совокупность оболочек с одним и тем же значением числа п - электронным слоем. Радиус оболочки, т.е. среднее расстояние от электрона до ядра, зависит от главного квантового числа п. Таким образом, волновые функции
с одинаковыми п и l называется оболочкой, а совокупность оболочек с одним и тем же значением числа п - электронным слоем. Радиус оболочки, т.е. среднее расстояние от электрона до ядра, зависит от главного квантового числа п. Таким образом, волновые функции  с одним и тем же значением п, но различными значениями l и т описывают электронные облака одного радиуса. Все эти облака принадлежат одному и тому же слою. Состояния с п = 1 образуют так называемый К-слой, состояния с п= 2 - L-слой, состояния с n = 3- М-слой, состояния с n= 4- N-слой и т.д. (табл. 2).
с одним и тем же значением п, но различными значениями l и т описывают электронные облака одного радиуса. Все эти облака принадлежат одному и тому же слою. Состояния с п = 1 образуют так называемый К-слой, состояния с п= 2 - L-слой, состояния с n = 3- М-слой, состояния с n= 4- N-слой и т.д. (табл. 2).
Таблица 2
| Число п | |||||
| Символ электронного слоя | К | L | M | N |
Состояния электрона с фиксированным значением п отличаются значениями квантовых чисел l, т и ms. При заданном значении l число т может принимать любое из 2 l + 1 значений - l,..., l. С учетом того, что спиновое квантовое число ms принимает два значения: ±1/2, число gnl состояний с фиксированными значениями nи l, т.е. число состояний
в оболочке, будет
gnl = 2(2 l +1). (21.33)
Число gn различных состояний, соответствующих данному значению п, т.е. число состояний в п-м слое, будет
gn = 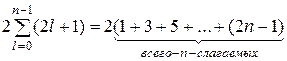
Слагаемые в круглых скобках суть члены арифметической прогрессии. Применяя известную формулу для суммы п членов арифметической прогрессии, получим:
gn = 2 n 2 . (21.34)
Классификация возможных состояний электрона в атоме приведена в табл. 3.
Таблица 3
| Слой | Число состояний в оболочке gnl = 2(2l+1) | 1) | Число состояний в слое | |||
| s l = 0 | p l = 1 | d l = 2 | f l = 3 | gn = 2 n 2 | ||
| К n= 1 | _ | - | _ | - | ||
| L n = 2 | _ | _ | - | |||
| М n = 3 | _ | _ | ||||
| N n = 4 | _ | |||||
Распределение электронов в атоме по состояниям осуществляется согласно принципу Паули, в силу которого в любой системе (например, в атоме) не может быть двух электронов, находящихся в одном и том же квантовом состоянии. Другими словами, какое-либо электронное состояние может быть либо свободно (т.е. не занято электроном), либо занято только одним электроном.
Основное, или невозбужденное состояние атома - это состояние с наименьшей энергией.
Описать состояние атома - это значит указать число электронов в каждом состоянии. Распределение электронов по состояниям называют электронной конфигурацией атома. Например, электронная конфигурация атома кобальта Со в основном состоянии символически записывается так:
1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 3 d 7 4 s 2
Здесь над символом электронного состояния указаны количества электронов в оболочке. Всего в атоме кобальта 27 электронов.
Электроны, находящиеся на внешнем слое атома, слабее связаны с ядром, чем внутренние электроны, расположенные ближе к ядру. Именно внешние электроны определяют химические свойства атома и строение его оптического спектра. Поэтому внешние электроны называют валентными, или оптическими электронами атома.
Возможные состояния электронов в атоме, классификация которых приведена в табл. 3, заполняются электронами в соответствии с принципом Паули. Руководствуясь этим принципом, можно установить электронные конфигурации атомов в основном состоянии. Знание электронных конфигураций атомов дает возможность объяснить химические свойства атомов и их расположение в периодической таблице элементов, открытой русским ученым Д.И.Менделеевым.
21.6. Векторная модель атома *
Воздействие внешнего магнитного поля на атом определяется его магнитным моментом, который обусловлен: 1) орбитальным движением электронов, 2) собственными магнитными моментами электронов и 3) магнитным моментом атомного ядра. Магнитный момент ядра существенно меньше магнитного момента электрона. Поэтому в данном случае его можно не принимать во внимание. Покажем, как можно вычислить магнитный момент атома.
Полный механический момент атома равен сумме орбитальных моментов импульсов всех электронов в атоме и их спинов:
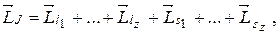 (21.35)
(21.35)
где Z - число электронов в атоме.
Вектор
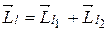
суммы двух моментов импульса обладает следующими свойствами. Модули векторов 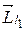 и
и 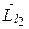 определяются квантовыми числами l 1 и l 2 согласно формулам
определяются квантовыми числами l 1 и l 2 согласно формулам
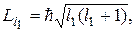
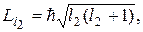
Модуль Li вектора суммы определяется аналогичной формулой
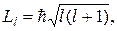
в которой квантовое число I может принимать следующие значения:
l = l 1 + l 2, l 1 + l 2 - 1, …, | l 1 – l 2| (21.36)
Предположим для определенности, что l 1 > l 2 В таком случае число l принимает одно из 2 l 2 + 1 значений:
l = l 1 + l 2, l 1 + l 2 - 1, …, l 1 – l 2
Проекцию Llz суммарного момента импульса на ось z можно найти пр формуле
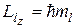 ,
,
где квантовое число то, принимает значения:
ml = - l - l + 1,…, l – 1, l.
Модуль и проекцию на ось z суммы нескольких моментов импульса можно найти, применяя последовательно описанные правила сложения двух моментов. Модуль и проекция на ось z вектора 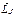 полного механического момента атома зависит от того, в какой последовательности осуществляется сложение векторов в формуле (21.35). Как показывает анализ экспериментального материала, для большинства атомов правильные значения модуля и проекции на ось z вектора
полного механического момента атома зависит от того, в какой последовательности осуществляется сложение векторов в формуле (21.35). Как показывает анализ экспериментального материала, для большинства атомов правильные значения модуля и проекции на ось z вектора 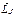 могут быть получены, если сначала сложить орбитальные моменты всех электронов:
могут быть получены, если сначала сложить орбитальные моменты всех электронов:
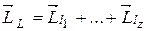 ,
,
отдельно сложить их спины:
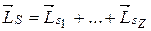 , L s — L Sl 4-... + L sz,
, L s — L Sl 4-... + L sz,
а затем сложить полученные таким образом полный орбитальный момент импульса 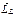 и полный спиновый момент
и полный спиновый момент 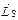
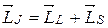
Такая схема вычислений отражает тип взаимодействия электронов в атоме, называемый (L, S) -связью.
Пусть модули векторов 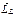 и
и 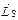 оказались равны
оказались равны

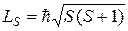 . (21.38)
. (21.38)
Так как орбитальные квантовые числа l 1, l 2,…, l Z отдельных электронов есть целые неотрицательные числа, квантовое число L согласно правилу (21.36) есть также целое неотрицательное число. Спиновые числа s 1, s 2,…, s Z отдельных электронов все равны 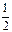 . Поэтому согласно правилу (21.36) квантовое число S полного спина атома может быть либо целым, либо полуцелым неотрицательным числом. Описанное правило сложения моментов приводит к следующей формуле для модуля вектора Lj суммарного момента импульса атома:
. Поэтому согласно правилу (21.36) квантовое число S полного спина атома может быть либо целым, либо полуцелым неотрицательным числом. Описанное правило сложения моментов приводит к следующей формуле для модуля вектора Lj суммарного момента импульса атома:
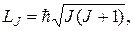 (21.39)
(21.39)
где квантовое число J может принимать значения:
J = L + S, L + S – 1, …, | L – S |. (21.40)
Проекция полного момента импульса атома на ось z будет
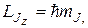 , (21.41)
, (21.41)
где квантовое число
mJ = - J, - J + 1, …, J – 1, J. (21.42)
В силу соотношения (21.20) полный орбитальный магнитный момент атома 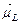 коллинеарен механическому орбитальному моменту
коллинеарен механическому орбитальному моменту 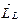 :
:
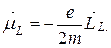
В силу соотношения (21.24) полный спиновый магнитный момент атома 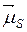 коллинеарен механическому спиновому моменту
коллинеарен механическому спиновому моменту 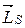 :
:
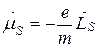 .
.
Полный магнитный момент атома  равен сумме полного орбитального магнитного момента
равен сумме полного орбитального магнитного момента 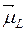 и полного спинового магнитного момента
и полного спинового магнитного момента 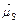 :
:
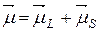 (21.43)
(21.43)
Нетрудно видеть, что вектор 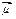 полного магнитного момента атома не коллинеарен вектору (21.37) полного механического момента атома. С течением времени вектор
полного магнитного момента атома не коллинеарен вектору (21.37) полного механического момента атома. С течением времени вектор 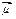 изменяет свое направление относительно вектора
изменяет свое направление относительно вектора 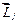 . Причем это изменение происходит таким образом, что среднее значение составляющей вектора
. Причем это изменение происходит таким образом, что среднее значение составляющей вектора 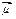 , которая перпендикулярна вектору
, которая перпендикулярна вектору 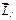 , оказывается равным нулю. Поэтому усредненный магнитный момент атома
, оказывается равным нулю. Поэтому усредненный магнитный момент атома 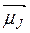 будет коллинеарен вектору полного механического момента:
будет коллинеарен вектору полного механического момента:
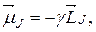 (21.44)
(21.44)
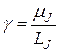 (21.45)
(21.45)
- гиромагнитное отношение для атома.
С учетом орбитального и спинового гиромагнитных отношений и формул (21.38) можно записать следующие выражения для модулей векторов 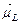 и
и 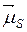
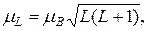
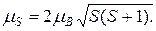
Модуль магнитного момента атома можно вычислить по формуле(21.46)
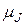 = g
= g 
где множитель
g = 1 + 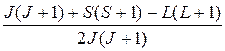
 (21.47)
(21.47)
называется множителем или фактором Ланде.
При помощи формул (21.39) и (21.46) найдем гиромагнитное отношение (21.45) для атома:
γ = gμВ / ħ = ge/2m
Из формул (21.41) и (21.44) следует, что проекция вектора 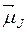 на ось z определяется квантовым числом mJ по формуле
на ось z определяется квантовым числом mJ по формуле
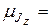 gμBmJ (21.49)
gμBmJ (21.49)
Классификация состояний (термов) атома производится по значениям, которые принимают квантовые числа L, S и J. Состояния атома с L = 0, 1, 2, 3,... обозначают соответственно буквами S, P, D, F,... (табл. 4).
Таблица 4
| Число L | … | ||||
| Символ состояния атома | S | Р | D | F | … |
Справа внизу у символа состояния указывается значение квантового числа J, а слева вверху - значение числа к = 2S+1, которое называется мулътиплетностпъю терма. Например, символ 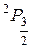 2Рз/2 обозначает состояние атома, для которого
2Рз/2 обозначает состояние атома, для которого
L = 1, J=3/2, S =1/2.
Равенство (21.44) служит основой для объяснения так называемых магнитомеханических явлений. Экспериментально установлено, что при быстром намагничивании тела оно начинает вращаться. Если же способное намагничиваться тело (например, железный стержень) достаточно быстро привести во вращение, то оно намагничивается. Такие эксперименты дают возможность измерить гиромагнитное отношение. Для атома железа оно оказалось равным е/т. Из этого следует, что магнитные свойства железа обусловлены собственными магнитными моментами электронов.
Date: 2015-05-19; view: 823; Нарушение авторских прав