Барьерные задачи

В данном разделе рассмотрим задачи, в которых потенциал внешнего поля принимает ограниченное значение во всем пространстве.

Прямоугольная потенциальная стенка.

Пусть потенциал V(x) задается следующим выражением:

причем величина V₀ может быть как положительной, так и отрицательной.

Пусть слева на такую потенциальную «ступеньку» падает частица с энергией E.

С точки зрения классической механики движение частицы носит строго детерминируемый характер: в случае E>V₀ (при V₀<0 это условие выполнено для всех E) частица пройдет через ступеньку в область x>0. Наоборот, при E<V₀ произойдет отражение частицы. В квантовой механике ситуация может быть не столь однозначной.

Рассмотрение квантовомеханической задачи мы начнем с решения стационарного уравнения Шредингера

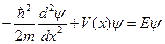
Поскольку потенциал V(x) является разрывной функцией, мы должны решить уравнение Шредингера в областях x < 0 и x > 0 и провести «сшивание» полученных решений, исходя из предположения, что в точке разрыва x = 0 волновая функция 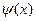и ее первая производная 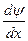непрерывны. С физической точки зрения такие условия означают непрерывность потока вероятности в точке разрыва потенциала.

Проведем рассмотрение поочередно для случаев E>V₀ и E<V₀.

a) E>V₀

Запишем стационарное уравнение Шредингера в областях x < 0 и x > 0 в виде:

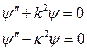
где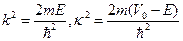

Общие решения уравнений

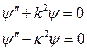
записываются в виде:

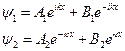
Волновая функция должна быть ограничена во всем пространстве. Поэтому следует положить 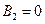. Раньше мы видели, что волновая функция вида

описывает поток частиц с плотностью

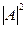
и скоростью

,

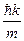движущийся в положительном направлении оси x. Поэтому функция 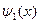в виде

означает, что слева от барьера существует два потока частиц: падающий на барьер и отраженный от него. Определим коэффициент отражения от барьера, как отношение этих потоков:

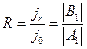
Для определения коэффициентов A и B проведем «сшивание» функци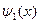й и 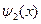в точке x=0. Получим:

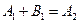
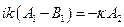
Выражая коэффициенты 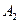и через (этот коэффициент определят плотность падающего потока), получим:

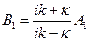
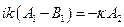
Тогда

,

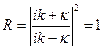а коэффициент прохождения

.

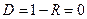Полученный результат непосредственно следует из выражений для 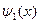и .

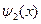
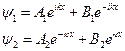Действительно:

,

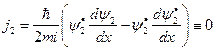а, следовательно, из непрерывности потока вероятности следует, что 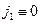, т.е. 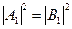или 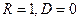. Эти результаты совпадают с результатами классического решения задачи об отражении частицы от потенциальной стенки, высота которой V₀ больше энергии частицы. Тем не менее, характер квантовомеханического решения задачи

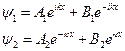
принципиально отличен от классического: в квантовой механике существует отличная от нуля вероятность обнаружить частицу в области x > 0. Эту величину можно вычислить так:

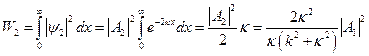
Эта вероятность тем больше, чем меньше величина V₀– E, и в случае неограниченно возрастает.

b) E > V₀

Поступая аналогично предыдущему случаю, запишем решение уравнения Шредингера в зонах x < 0 и x > 0 в виде:

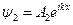
где ,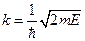

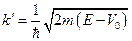
Заметим, что в области x > 0 в общем случае следовало бы записать слагаемые, описывающие волны, бегущие как направо, так и налево. Однако, мы, исходя из физической постановки задачи, предположили, что волна, движущаяся в отрицательном направлении оси x, отсутствует.

Проведя «сшивание» функци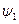й и 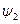и их производных при x = 0, получим:

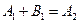
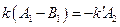
откуда:

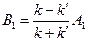
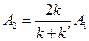
Определим, наконец, коэффициенты отражения и прохождения частицы:

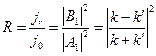
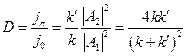
При этом, как легко увидеть,

R + D = 1.

Полученный нами результат существенно разошелся с результатом, ожидаемым с классической точки зрения. Действительно при E > V₀ мы бы получили 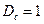, 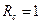. Однако, в случае классическое и квантовое решение задачи совпадают: разлагая выражения

,

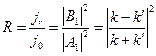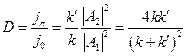
в ряд по малому параметру

,

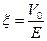получим:

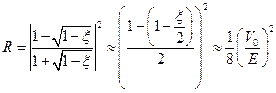
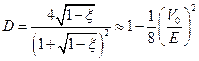
Полученные зависимости 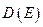для классического и квантового случаев приведены на рисунке:

Вероятность прохождения потока частиц через «потенциальную ступеньку» в зависимости от энергии частицы (пунктир – классический результат)

Как видно, существенное отличие результатов наблюдается лишь в достаточно узком интервале энергий частицы вблизи V₀.

Рассмотренная нами стационарная картина процесса неадекватна постановке задачи о движении классической частицы (материальной точки) в поле «потенциальной ступеньки». Действительно, использованное выше представление о потоке частиц с заданной энергией с математической точки зрения означает задание волновой функции в виде плоской волны, т.е. исключает вопрос о локализации частицы в какой-либо области пространства. В результате за рамками рассмотрения остается вопрос о пространственно-временной картине движения частицы в потенциальном поле. Изучение такой картины процесса желательно как с точки зрения прямого сопоставления классического и квантового решения рассматриваемой задачи, так и в связи с невозможностью в рамках традиционного стационарного подхода дать ответ на ряд вопросов, возникающих при изучении явления. Например, было бы интересно увидеть, где локализована частица в «момент» (в процессе) рассеяния и какова длительность этого процесса, как при этом изменяется ее скорость движения, каковы скорость прошедших и отраженных частиц, где и с какой вероятностью мы обнаружим частицу в конкретный момент времени.

Ответ на эти вопросы может дать только решение нестационарного уравнения Шредингера.

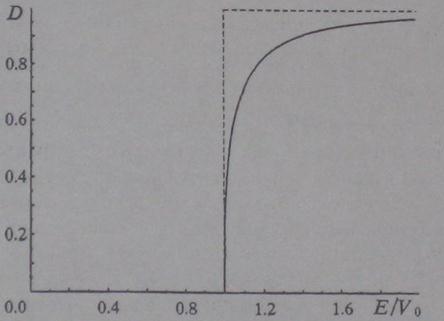
Математическая постановка задачи заключается в следующем: мы должны решить уравнение:

,

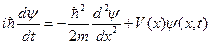где потенциал 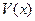задается выражением 3.1.1, а волновая функция начального состояния

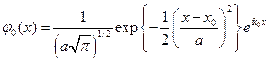
К лабораторным работам. Пакет «NSSE»

Главное меню пакета «NSSE»

Всюду, если это особо не оговаривается, начальное состояние частицы определяется как

,

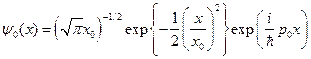где 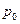– импульс частицы, 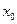– ширина начального распределения. При этом вместо величины 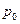вводится энергия

,

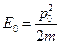задаваемая в качестве начального условия.

Число пространственных точек, на которых ищется решение уравнения Шредингера, составляет 64, 128 или 256. Пользователь может ввести числа 1, 2 или 3, что соответствует поиску решения уравнения Шредингера на 64, 128 ли 256 точках.

В процессе демонстрации на экран выводится потенциальных профиль 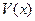, величина 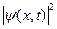, определяющая распределение плотности вероятности обнаружить частицу в различных точках пространства, другая необходимая информация.

Классическое движение частицы в потенциале 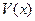моделируется с помощью уравнения

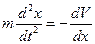
Все необходимые команды, которые могут быть использованы при работе с пакетом, высвечиваются на дисплее. Задействованы следующие клавиши:

Свободное движение частицы.

Меню процесса №1

Данная программа демонстрирует квантовомеханическое движение частицы (электрона) в отсутствие внешних полей. Для пуска программы необходимо лишь задать начальное состояние частицы, которое характеризуется двумя параметрами: 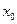– ширина начального распределения и 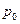– импульс частицы. В пакете вместо величины 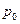вводится энергия .

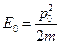В процессе решения уравнения Шредингера помимо величины 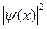на дисплей выводится текущее время, ширина волнового пакета и энергия частицы 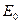, а также положение классической частицы.

Свободное движение частицы

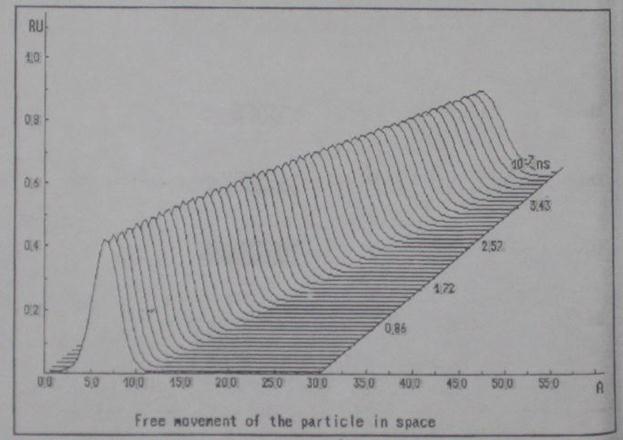
График функции 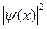для процесса №1

Движение частицы через потенциальную ступеньку.

Данная программа предназначена для изучения движения частицы в потенциале виды

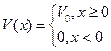
Для запуска программы необходимо задать волновую функцию начального состояния, характеризуемую параметрами 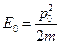и 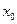, а также высоту «потенциальной ступеньки» 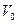. Величина 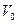может быть как больше (налетание частицы на потенциальный барьер), так и меньше нуля (скатывание частицы в потенциальную яму).

В процессе решения задачи на дисплей выводятся графики функций 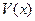, , 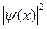а также положение классической частицы. При нажатии клавиши F1 на экран выводятся также вероятности обнаружить частицу справа (transmissivity) и слева (reflectivity) от «потенциальной ступеньки», определяющие коэффициенты отражения и прохождения соответственно.

Меню процесса №8

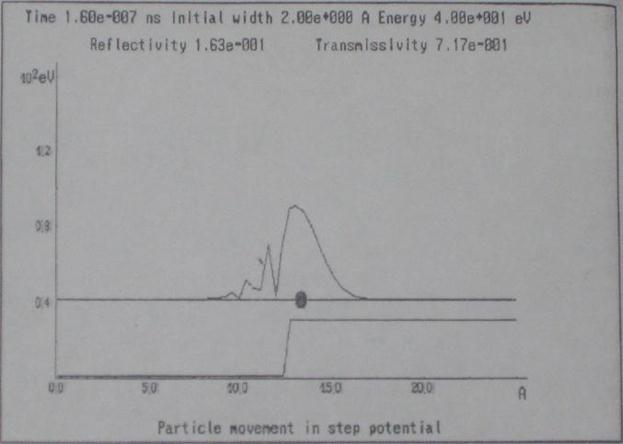
Движение частицы через «потенциальную стенку»

ГЛАВА 21

Date: 2015-05-19; view: 1085; Нарушение авторских прав