Спектр энергии и волновые функции электрона в атоме водорода

Атом водорода представляет задачу двух тел – квантовый аналог задачи Кеплера в классической механике. Потенциальная энергия взаимодействия электрона с протоном определяется законом Кулона:

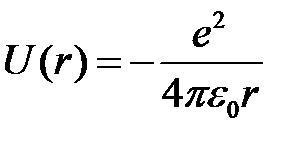. (1)

Из-за большой разницы масс электрона и протона последний можно считать неподвижным, а электрон - движущимся в независящем от времени потенциальном поле U (r) (1), которое зависит только от расстояния 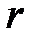электрона до центра (протона). Таким образом, атом водорода представляет пример движения частицы в центрально-симметричном потенциальном поле. Как известно, в таком поле помимо энергии E_n сохраняется квадрат углового момента M ²= ħ ² l (l +1) и проекция углового момента на ось 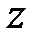: M_z = ħm, где l и m – орбитальное и магнитное квантовые числа соответственно. Поэтому волновая функция электрона в атоме водорода является одновременно собственной функцией операторов 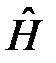, 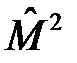и 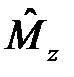. В сферической системе координат волновую функцию электрона можно представить в виде:

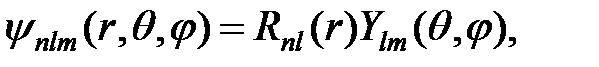(2)

где 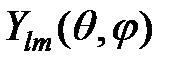– сферические функции – собственные функции оператора :

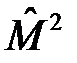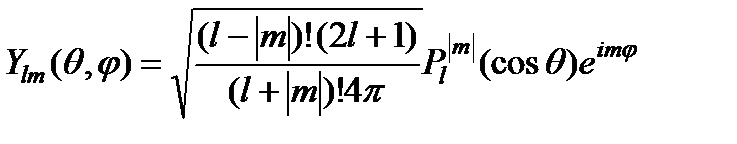. (3)

Радиальная волновая функция R_nl (r) определяется видом потенциальной функции U (r). Физический смысл угловой и радиальной составляющих волновой функции можно выяснить, подставляя (2) в условие нормировки:

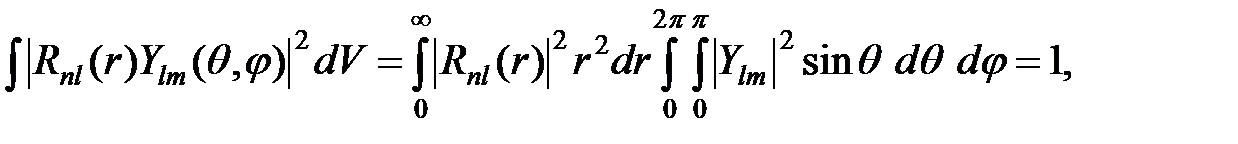(4)

где 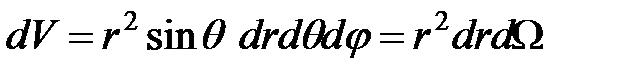– элемент объёма в сферической системе координат, а 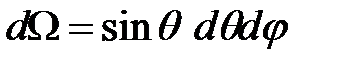– элемент телесного угла.

Так как сферические функции нормированы, то

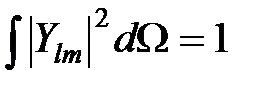. (5)

Отсюда получаем условие нормировки для радиальной волновой функции:

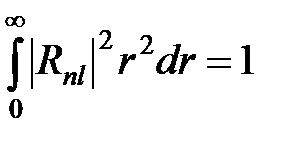. (6)

Равенство (5) выражает условие нормировки для сферических функций и (6) – для радиальной волновой функции, откуда ясно, что 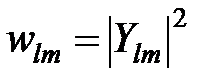есть угловая плотность вероятности, т.е. вероятность обнаружить электрон в единице телесного угла, а 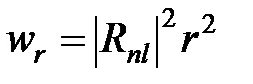есть радиальная плотность вероятности, т.е. вероятность обнаружить электрон в сферическом кольце единичной толщины, а 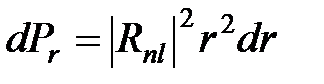– вероятность найти электрон в бесконечно тонком, толщиной dr сферическом кольце радиусом r.

Запишем теперь уравнение Шрёдингера в сферической системе координат:

.

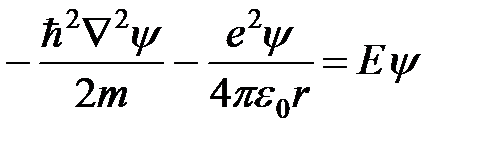Учитывая, что ,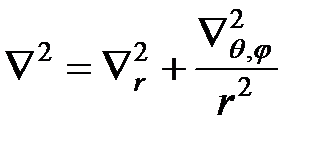

где 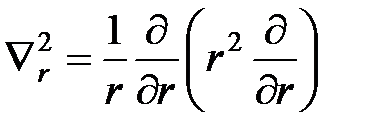; 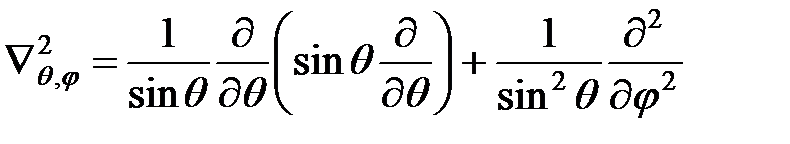, получим

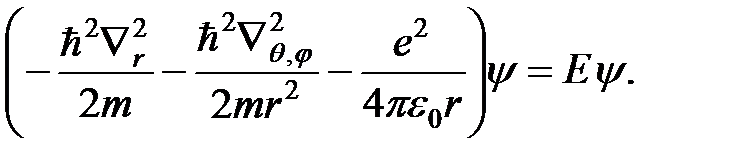
Так как оператор 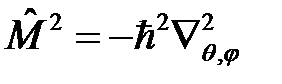, а 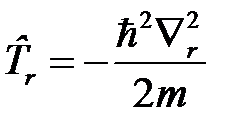– оператор кинетической энергии движения электрона по радиусу-вектору, то

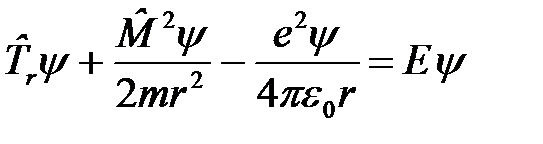. (7)

Сферические функции Y_lm являются собственными функциями оператора 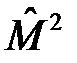, поэтому

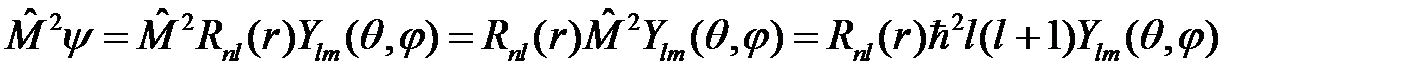. Подставляя в уравнение (7), после сокращения на Y_lm получим радиальное уравнение Шрёдингера:

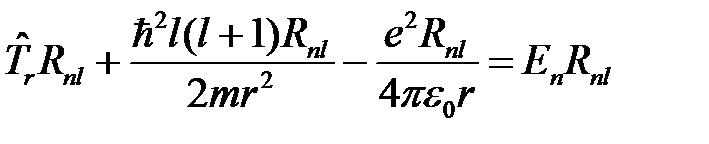. (8)

1. Спектр энергии атома водорода

Собственные значения энергии электрона:

,

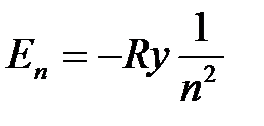где 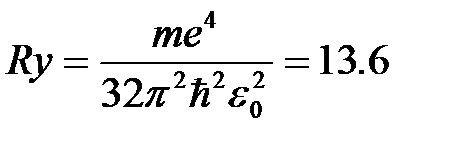эВ – постоянная, называемая Ридбергом.

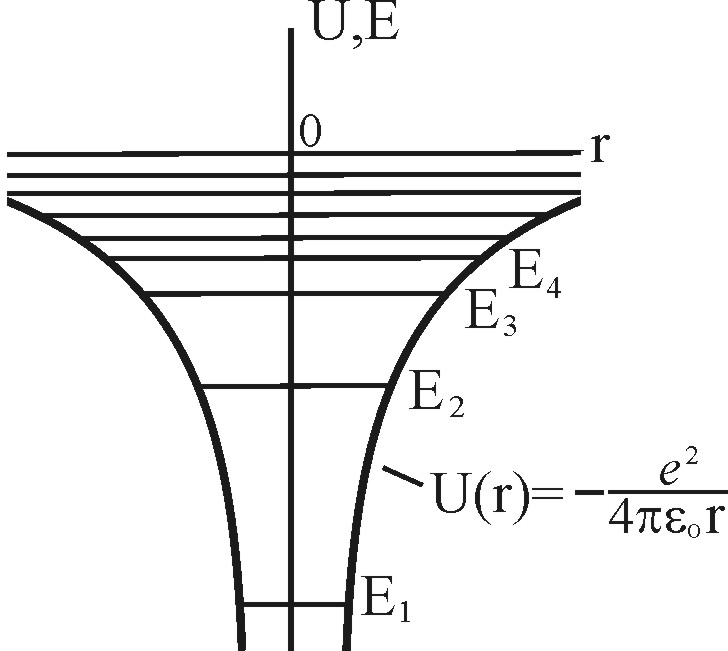
Рис. 3.1. Гиперболическая потенциальная яма и спектр энергии атома водорода

Ридберг численно равен энергии ионизации атома водорода I = Ry. Переходы электрона с любого возбужденного уровня на уровень E ₁, дают спектральную серию Лаймана, с любого на Е ₂ – серию Бальмера, далее на третий Е ₃ – серию Пашена и т. д.

Таким образом, спектр излучения (поглощения) атома водорода – дискретный, т. е. состоит из отдельных спектральных линий, отвечающих переходам между дискретными энергетическими уровнями электрона.

2. Радиальные волновые функции

Решениями радиального уравнения Шрёдингера (8) являются радиальные волновые функции, выраженные через безразмерную координату 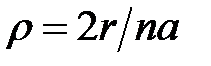, где a = ħ ²/ me ² – первый боровский радиус.

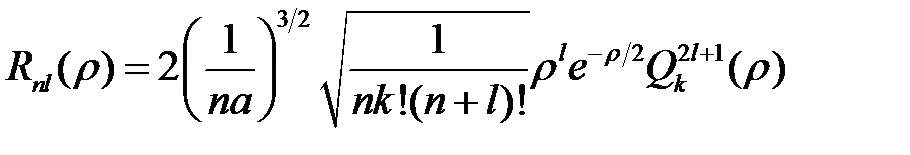, (9)

где 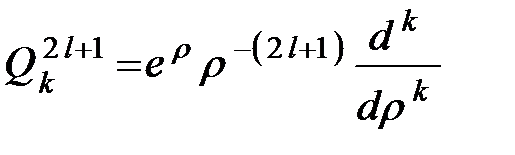(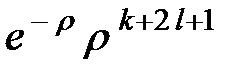) – полином Лагерра, k – радиальное квантовое число, равно числу узлов радиальной волновой функции R_nl (r), n = l + k +1 – главное квантовое число, l – орбитальное квантовое число. Волновые функции с l = 0,1,2,3… 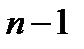обозначается соответственно как s, p, d, f … состояния.

Date: 2015-05-19; view: 1802; Нарушение авторских прав