Заряд в магнитном поле

Магнитное поле изменяет фазу волновой функции заряда и длину волны де Бройля. Это используется для измерения эффективной массы и магнитного момента носителя тока в кристалле методом циклотронного резонанса, для определения поверхности Ферми и концентрации электронного газа.

Квазиклассическое квантование в магнитном поле. Фаза волновой функции и длина волны де Бройля определяются полным импульсом 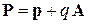, тогда квантование Бора–Зоммерфельда дает

,

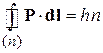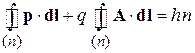, (1.21)

Циклотронная частота. Заряд q движется со скоростью V 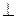В. Сила Лоренца 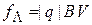перпендикулярна магнитному полю В и скорости. Это центростремительная сила

.

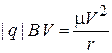Заряд движется по окружности радиусом

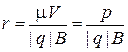. (1.23)

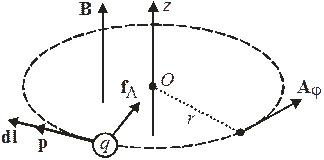
Заряд 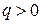в магнитном поле

Угловая скорость или циклотронная частота

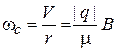. (1.24)

Поле выражается через векторный потенциал 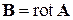. В цилиндрических координатах

, , .

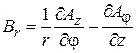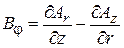Для однородного поля 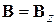выбираем калибровку

, , .

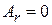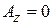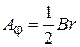Из 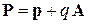и рис. получаем соотношение между модулями полного и кинетического импульсов

,

.

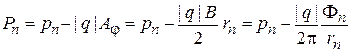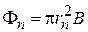Используем

,

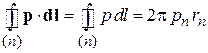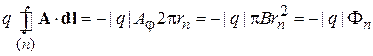
и из (1.21) находим условие квантования

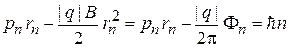. (1.25)

Квантование импульса, момента импульса, энергии и радиуса траектории. Из (1.25) и (1.23) получаем квантование кинетического импульса

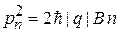. (1.26)

Условие квантования (1.19) 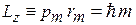выполняется в магнитном поле для момента полного импульса

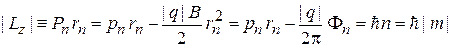, (1.27)

где m – магнитное квантовое число, тогда

.

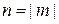Из (1.23) и (1.26) следует квантование радиуса траектории

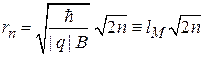, (1.29)

где магнитная длина

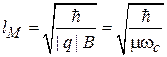(1.30)

Для электрона 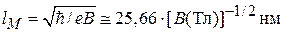. Магнитное поле у земли 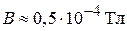и для него .

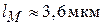Квантование магнитного потока. Используя (1.29), находим магнитный поток через площадь, ограниченную траекторией:

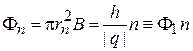, (1.31)

где квант магнитного потока

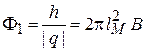. (1.32)

Согласно (1.31) квантовое число n равно числу квантов магнитного потока, приходящихся на площадь, ограниченную траекторией заряда. В сверхпроводнике заряд спаренных электронов 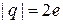, тогда квант магнитного потока в сверхпроводнике

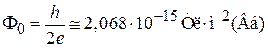. (1.33)

Ф₀ приблизительно равен потоку 1/100 магнитного поля земли через площадку диаметром 0,1 мм.

Квантование магнитного потока обосновали В.А. Фок и П. Иордан в 1930 г., Ф. Лондон в 1948 г. Экспериментально явление обнаружили в сверхпроводнике Б. Дивер и В. Фейрбэнк в 1961 г.

Квантование сопротивления. Для контура с током, плоскость которого перпендикулярна магнитному полю, используем баланс энергии. Приложенное к концам контура напряжение U поддерживает в цепи ток I и при переносе заряда q совершает работу 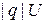. При увеличении магнитного потока на 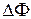, возникает явление электромагнитной индукции и для поддержания тока источник совершает работу 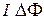, тогда 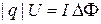. В цепи возникает индуктивное сопротивление

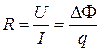. (1.35)

Если ток переносится электронами 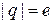, то кванту магнитного потока 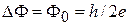соответствует квант сопротивления

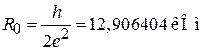. (1.36)

Потоку (1.32) 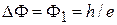соответствует холловское сопротивление

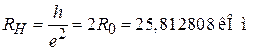. (1.36а)

Квантование сопротивления баллистического проводника, в котором электроны движутся без рассеяния: 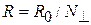, где 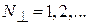– число активизированных поперечных мод движения, обосновал Р. Ландауэр в 1970 г. Баллистическая проводимость наблюдается в многослойной углеродной нанотрубке. Сопротивление нанотрубки не зависит от ее диаметра и длины и равно кванту сопротивления, если длина трубки не превышает длины свободного пробега электрона в несколько микрометров. Углеродные нанотрубки допускают плотности тока до 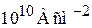и пропускают ток без деградации в течение недель; золото, серебро и медь выдерживают токи до 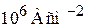, далее они плавятся.

Квантование магнитного момента. Контур с током создает магнитный момент, равный произведению силы тока на площадь контура и направленный перпендикулярно плоскости контура по правилу правого винта. Модули магнитного момента 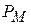и момента импульса L заряда, создающего ток, взаимно пропорциональны 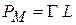, где 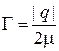– гиромагнитное отношение, известное из классической физики. Используя (1.27), получаем модуль и проекцию орбитального магнитного момента электрона

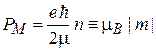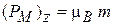, , (1.37)

где магнетон Бора

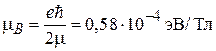(1.38)

введен Вольфгангом Паули в 1920 г. Следовательно, проекция орбитального магнитного момента на направление поля пропорциональна магнитному квантовому числу m.

Подстановка Пайерлса. В магнитном поле длина волны де Бройля определяется полным импульсом (1.20) 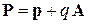, который складывается из кинетического импульса 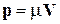и импульса магнитного поля 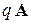, в котором находится заряд q. При изменении поля меняется векторный потенциал A и скорость заряда за счет явления электромагнитной индукции, полный импульс сохраняется и ему сопоставляется оператор неизменной формы

.

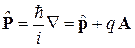Действие магнитного поля на квантовую систему учитывается подстановкой Пайерлса

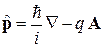, (5.39)

когда заменяется оператор кинетического импульса 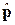в формулах, описывающих систему без магнитного поля. Гамильтониан и уравнение Шредингера получают вид

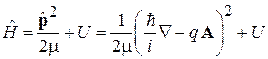, (5.40)

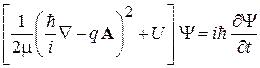. (5.41)

Date: 2015-05-19; view: 665; Нарушение авторских прав