Уровни Ландау. Состояния заряда в однородном магнитном поле получил Л.Д

Состояния заряда в однородном магнитном поле получил Л.Д. Ландау в 1930 г.

Гамильтониан (5.40)

.

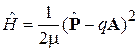В декартовых координатах для поля , с учетом 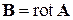, в частности 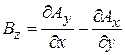, используем

,

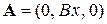тогда

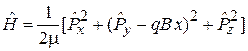. (5.46)

Уравнение Шредингера 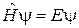получает вид

.

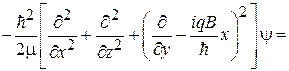
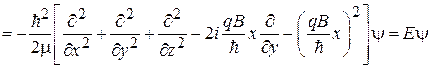Операторы 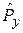и 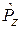коммутируют с 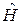, тогда решение содержит произведение собственных функци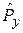й и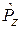

,

.

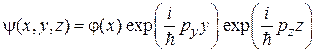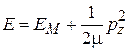Если движение по оси z не ограниченное, то 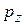– любое вещественное число. Подстановка решения в уравнение и деление его слева на ψ дает уравнение для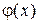

,

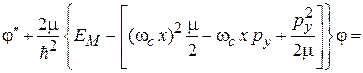
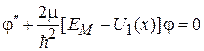где 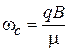– циклотронная частота (1.23). Эффективная потенциальная энергия

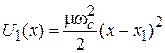
соответствует потенциальной энергии гармонического осциллятора (3.23), колеблющегося около точки:

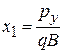(5.47)

с частотой 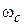и с амплитудой (3.40) нулевых колебаний 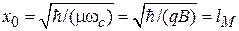, где 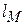– магнитная длина. Из (3.32) получаем

,

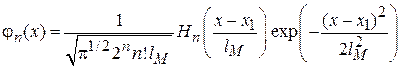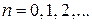
Уровни Ландау. Спектр энергии движения в плоскости 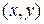совпадает со спектром гармонического осциллятора. Из (3.39) находим

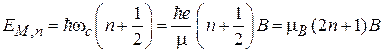. (5.48)

Число состояний на уровне Ландау. Состояние зависит от положения центра циклотронного движения 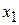, энергия (5.48) не зависит от 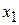, поэтому уровень Ландау вырожден. Для движения в области 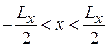, 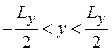условие 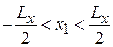на центр (5.47) ограничивает импульс интервалом 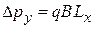. Пространственное ограничение по оси y вызывает квантование 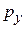. Граничное условие Борна–Кармана (3.8) требует

,

, ,

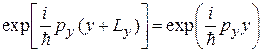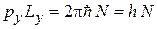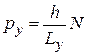где N – целое число. Допустимые значения импульса имеют шаг 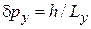. Учитывая степень вырождения σ состояний по спину и (1.32) , находим кратность вырождения уровня n

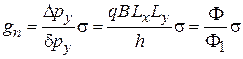. (5.52)

Число состояний на уровне Ландау пропорционально числу квантов магнитного потока, приходящихся на область, доступную для движения заряда.

Date: 2015-05-19; view: 484; Нарушение авторских прав