Эффект Ааронова–Бома

Магнитное поле и электрическое поле выражаются через потенциалы

,

,

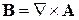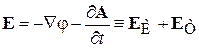где

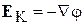– потенциальное поле Кулона;

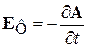– вихревое поле Фарадея.

В области, где

, ,

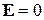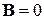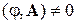
заряд не подвергается силовому воздействию и не изменяет своего состояния согласно классической электродинамике. Дэвид Бом и Якир Ааронов показали в 1959 г., что фаза волновой функции заряда изменяется под действием скалярного и векторного потенциалов, даже в том случае, когда нет силового действия поля на частицу. Изменение фаза обнаруживается в интерференционных явлениях. Магнитный эффект Ааронова–Бома подтвердили экспериментально R.G. Chambers в 1960 г., A. Tonomura в 1982 г., электрический эффект – G. Matteucci и G. Pozzi в 1985 г. Влияние полей Е и В, не равных нулю только в области, где нет частицы, на ее состояние свидетельствует о нелокальности квантового состояния – оно присутствует во всем пространстве и реагирует на внешние воздействия. Эффект Ааронова–Бома является квантовым явлением.

Якир Ааронов (1932) Дэвид Бом (1917–1992)

Полуклассическое рассмотрение. Заряд q движется перпендикулярно магнитному полю В по круговой траектории

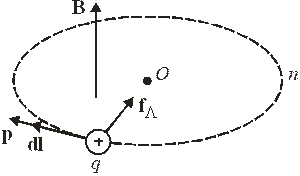
Используем условие квантования полного импульса (1.21) на траектории n

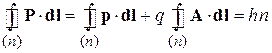. (7.35)

Текущая фаза частицы, движущейся с импульсом Р из точки 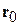в точку 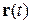, равна

.

Из (7.35) получаем, что при прохождении замкнутой траектории n с импульсом Р фаза волны увеличивается на

.

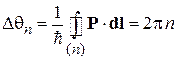Это условие максимума интерференции, волна усиливается, вероятность обнаружения частицы в точках траектории максимальна. Набранная фаза согласно (7.35) состоит из двух слагаемых. Перемещение в пространстве дает вклад

,

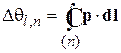магнитное поле меняет фазу на

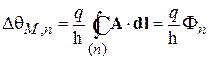. (7.36)

В последнем равенстве использована теорема Стокса – циркуляция векторного потенциала А по замкнутому контуру L равна потоку вектора В через площадку S, ограниченную контуром:

.

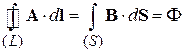Для незамкнутой траектории между точками r ₀ и r поток обобщается

,

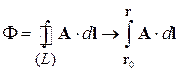где интеграл берется по траектории. Тогда при перемещении частицы из точки 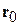в точку 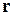изменение фазы за счет магнитного поля

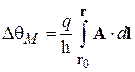. (7.37)

Векторный потенциал изменяет фазу волновой функции заряда, что является эффектом Ааронова–Бома.

Фаза волны измеряется в интерференционных экспериментах. Соотношение (7.37) позволяет измерить векторный потенциал. Выбираем участок с 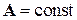, получаем

,

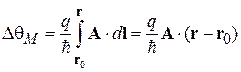и находим A. В квантовой механике векторный потенциал измерим. В классической электродинамике измерима лишь циркуляция по замкнутому контуру, равная магнитному потоку:

.

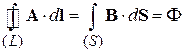Магнитный эффект в квантовой механике. Рассмотрим плоский заряженный ротатор в виде заряда, движущегося по проволоке в форме кольца, расположенного симметрично вокруг бесконечно тонкого и длинного соленоида. Силовые линии сосредоточены внутри соленоида и рассеиваются на бесконечности. Вне соленоида на малом расстоянии по сравнению с его длиной поле 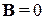и отсутствует силовое действие поля на ротатор.

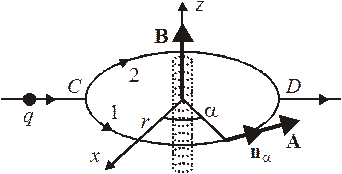
Поле соленоида в цилиндрических координатах

,

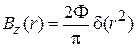где Ф – магнитный поток через поперечное сечение соленоида. Для доказательства вычисляем поток в цилиндрических координатах

.

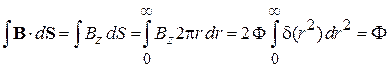Для нахождения векторного потенциала соленоида используем теорему Стокса

.

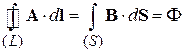Для контура L радиусом r находим циркуляцию A

,

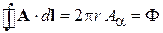тогда в цилиндрических координатах

, , , .

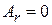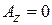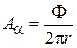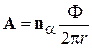Векторный потенциал образует правый вихрь вокруг соленоида.

Для стационарного состояния ротатора с зарядом q, с энергией E, находящегося в кольце радиусом r, используем уравнение Шрёдингера (7.18)

,

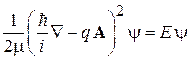В полярных координатах (r,α) при 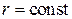используем

, .

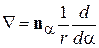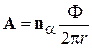Для 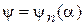получаем уравнение

,

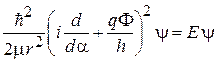где

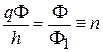
– число квантов магнитного потока через поперечное сечение соленоида. Решение ищем в виде

,

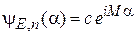где 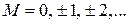обеспечивает периодичность

.

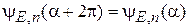Подстановка решения в уравнение дает

,

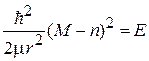тогда

.

Силовое действие поля на частицу отсутствует, поэтому спектр энергии не может отличаться от энергии плоского ротатора без соленоида

,

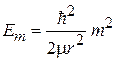тогда 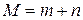. Волновая функция

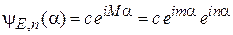
содержит множитель 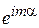, связанный с перемещением в пространстве, и вклад магнитного поля 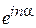. Следовательно, магнитное поле изменяет фазу волновой функции

,

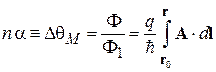что совпадает с (7.37).

Электрический эффект. Произвольное стационарное состояние с полной энергией E имеет вид

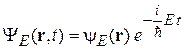
Фаза волновой функции изменяется с течением времени пропорционально полной энергии

.

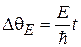Заряд q, находящийся в электрическом поле с потенциалом 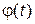, имеет потенциальную энергию 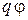. За время τ заряд набирает фазу

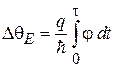. (7.39)

Электрический потенциал изменяет фазу волновой функции.

Эксперимент. Электрон в виде волнового пакета испускается в т. A, проходит через отверстия экрана 1 и 2, и движется внутри проводящих цилиндров – цилиндров Фарадея, экранирующих внешнее электрическое поле Е. За время движения электрона внутри цилиндров поле между цилиндрами включается, поддерживается постоянным в течение времени τ, и затем отключается. На всех этапах силовое воздействие на электрон отсутствует, электрон получает только потенциальную энергию 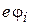, определяемую потенциалом цилиндра 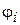, где .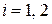

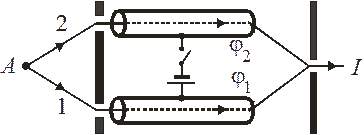
Согласно (7.39) на путях 1 и 2 набирается разность фаз

,

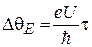где 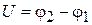– разность потенциалов цилиндров. Интерференция токов 1 и 2 создает максимальный общий ток I при разности фаз

,

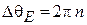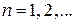
тогда

.

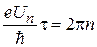Напряжение между цилиндрами при максимальном токе

.

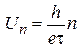Изменение напряжения приводит к осцилляции тока и сопротивления цепи с периодом

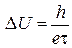, (7.40)

где τ – длительность включенного напряжения между цилиндрами. Эксперименты G. Matteucci и G. Pozzi, выполненные в 1985 г., подтвердили этот вывод.

Date: 2015-05-19; view: 1650; Нарушение авторских прав