Электрон в периодической структуре

Сближение N одинаковых потенциальных ям приводит к туннельному перемещению электрона между ямами и вызывает расщепление каждого уровня одиночной ямы на N подуровней. Множество подуровней называется зоной. Основы зонной теории кристалла заложили Ф. Блох и Л. Бриллюэн в 1928 г. и Р. Пайерлс в 1930 г. Задачу о движении электрона в периодическом поле, моделирующем кристаллическую решетку, рассмотрели в 1931 г. Р. Крониг и В. Пенни. Электрон в кристалле является свободной квазичастицей, движущейся с групповой скоростью и квазиимпульсом, и имеющей эффективную массу, отличающуюся от массы свободного электрона.

Расщепление уровня при сближении ям. Рассмотрим две δ-образные ямы на расстоянии 2 l друг от друга

,

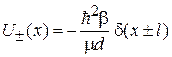где 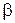– борновский параметр. Для одиночных ям существует единственное связанное состояние (П.3.15–16)

, .

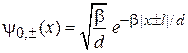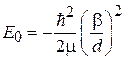Две ямы 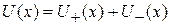образуют симметричную систему 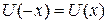, поэтому существуют линейно независимые четное 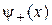и нечетное 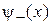состояния. При большом расстоянии между ямами 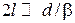, где 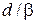– расстояние, на котором существенно убывает волновая функция, пренебрегаем изменением волновой функции электрона, вызванным соседней ямой. Для системы ям получаем четную и нечетную суперпозиции

.

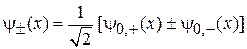Энергии состояний

.

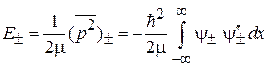Интегрирование по участкам 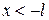, , 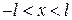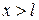дает

, .

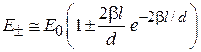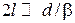Экспоненциальный множитель обусловлен туннельным переходом электрона между ямами. Уровень Е ₀ одиночной ямы расщепляется на уровн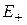и и 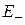, четный уровень находится ниже нечетного 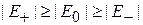. Степень расщепления уровней

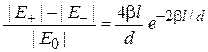
возрастает при ослаблении ям (уменьшении β ) и при их сближении. С течением времени электрон периодически переходит между ямами с периодом

.

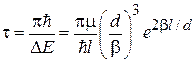Одномерная решетка имеет узлы, создающие барьеры для электрона. Для неограниченной решетки из δ-образных барьеров

,

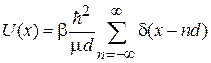где 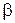– степень непроницаемости барьера; 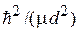– параметр с размерностью энергии; m – масса свободного электрона; d – постоянная решетки.

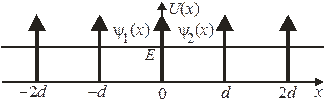
Волна Блоха. Уравнение Шредингера (3.1) получает вид

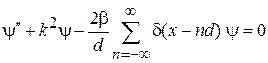, (3.75)

где 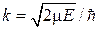– волновое число. Решение ищем в виде бегущей волны 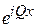, модулированной функцией в пределах каждого периода:

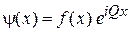, (3.76)

где Q – квазиволновое число. Волновую функцию (3.76) предложил Ф. Блох в 1928 г.

Потенциальная энергия не изменяется при замене 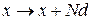, где N – целое число, тогда

.

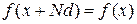Из (3.76) получаем

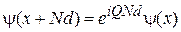, (3.77)

.

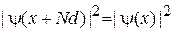Электрон обнаруживается в пределах каждого периода решетки с одинаковым распределением вероятности.

Волновые функции соседних интервалов. При 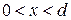уравнение (3.75) 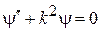имеет общее решение

.

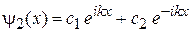Для 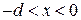находим 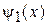с помощью (3.77) при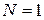

,

,

.

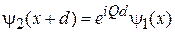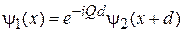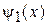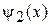Дисперсионное соотношение. Сшиваем и при 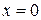. Условия (3.11)

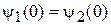
дает

.

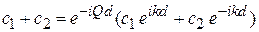Из (3.13)

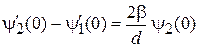
получаем

.

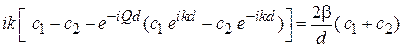Система уравнений для 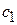и 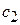имеет вид

,

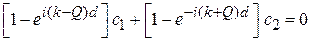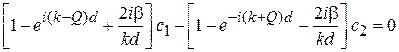. (3.78)

Условие совместности (3.78) обращает в нуль определитель коэффициентов и дает дисперсионное соотношение

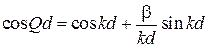. (3.79)

Оно связывает локальное волновое число электрона

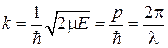
с интегральным квазиволновым числом Q.

Разрешенные и запрещенные зоны. Условие 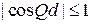ограничивает правую сторону (3.79)

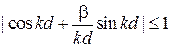. (3.80)

Области значений kd, удовлетворяющие (3.80), называются разрешенными зонами 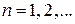, и обозначены на рисунке отрезками толстых линий. Между ними находятся запрещенные зоны.

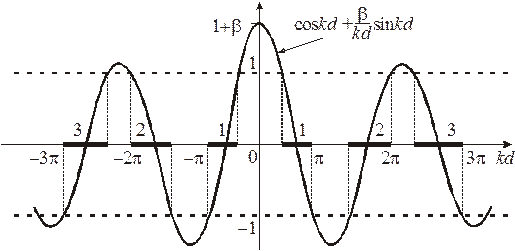
Верхняя граница разрешенной зоны. С увеличением k переход от разрешенной к запрещенной зоне происходит при , , ,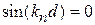

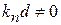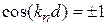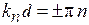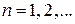, (3.81)

При этом, согласно (3.79), волновое число совпадает с квазиволновым числом

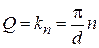. (3.82)

Выражаем (3.81) через длину волны де Бройля

.

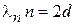Это есть условие Вульфа–Брегга (П.1.2) 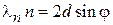для максимума отраженной волны при угле скольжения 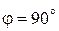, т. е. при нормальном падении на кристалл. У верхней границы разрешенной зоны электрон испытывает брэгговское отражение и не распространяется по кристаллу. Интенсивности падающей волны 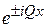и отраженной 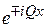равны. Их интерференция дает стоячие волны. Если при отражении фаза волны не меняется, то стоячая волна четная

,

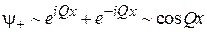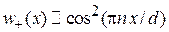
и электроны скапливаются вблизи ионов. Электростатическое взаимодействие электрона с ионом 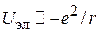изменяет энергию кристалла – она понижается на 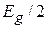по сравнению с равномерным распределением электронов. Если при отражении фаза волны увеличивается на p, то стоячая волна нечетная

, ,

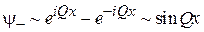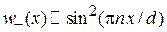электроны скапливаются между ионами, энергия кристалла повышается на 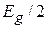. Это состояние принадлежит следующей разрешенной зоне. Между ними находится запрещенная зона шириной .

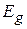Электрон как квазичастица. Электрон характеризуется массой m, волновым числом k, импульсом p и скоростью v. Электрон в кристаллерассматривается как квазичастица с эффективной массой m*, квазиволновым числом Q, квазиимпульсом P, групповой скоростью V. Импульс электрона изменяется под действием поля решетки и внешнего поля. Квазиимпульс 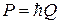изменяется только внешним полем. Для определения характеристик квазичастицы в зоне n получим энергию как функцию квазиволнового числа 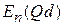для частных значений параметра .

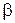1) Абсолютно свободный электрон, барьеры отсутствуют, 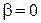. Соотношение (3.79)

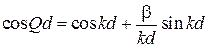
в виде

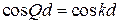
не ограничивает k и дает 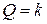. Спектр непрерывный

,

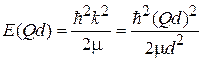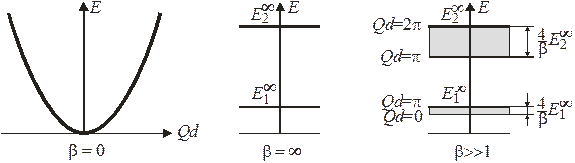
показан на рис. 1. Электрон обнаруживается в любой точке решетки с одинаковой вероятностью.

2) Абсолютно связанный электрон, барьеры не проницаемые, 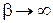. Соотношение (3.79) имеет смысл, если 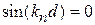, , 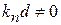тогда

,

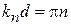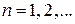
Решетка распадается на изолированные ямы шириной d с дискретным спектром

,

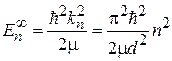показанным на рис. 2.

1 2 3

3) Приближение сильной связи 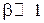близко к предыдущему случаю, тогда

, ,

, .

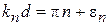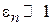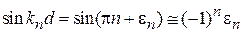Из (3.79) получаем

, .

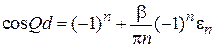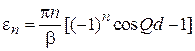Учитывая 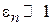, находим

.

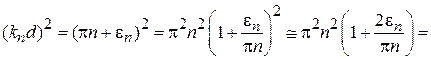
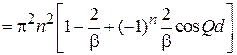Подстановка в 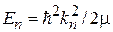дает

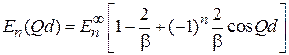. (3.83)

При фиксированном n состояния с разными Q и Е образуют разрешенную зону, как показано на рис. 3. Выполняется

, .

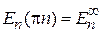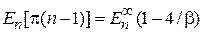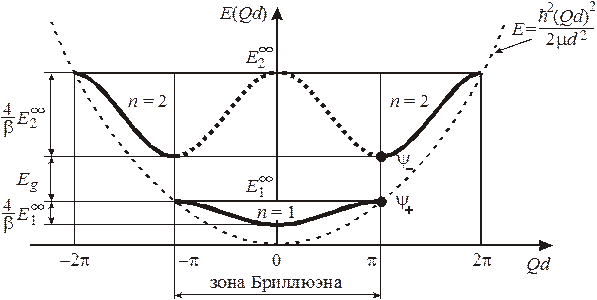
Энергетические зоны. График 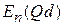для первых двух зон показан на рисунке толстыми сплошными линиями. Верхняя граница зоны 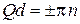касается параболы 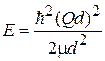, показанной пунктиром, где выполняется условие 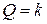. Ширина разрешенной зоны

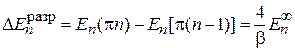. (3.84)

Чем больше степень непроницаемости барьера β, тем меньше ширина разрешенной зоны.

Ширина запрещенной зоны, или энергетической щели:

.

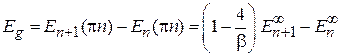Появление щели объясняется тем, что при 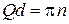возникают два типа стоячих волн – четная ψ₊ и нечетная ψ_–. Уровень, соответствующий исходной бегущей волне, распадается на два уровня, принадлежащих соседним разрешенным зонам.

Замена

,

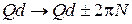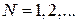
не меняет функцию (3.83). Передвигаем левую и правую ветви зоны 2 на ±2π, соответственно. Результат показан толстой пунктирной кривой. Первая и вторая зоны, и аналогично другие зоны, попадают в интервал 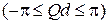, называемый первой зоной Бриллюэна. Квазиимпульс достаточно рассматривать в пределах этой зоны. На краю зоны квазиимпульс 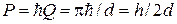и при d» 3×10^–8 см энергия края зоны 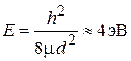близка к энергии Ферми электронного газа металла.

Для кристалла с конечной макроскопической протяженностью L волновая функция электрона удовлетворяет условию Борна–Кармана (3.8)

.

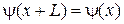Тогда с учетом 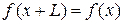, у волны Блоха (3.76) 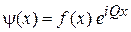квантуется квазиволновое число 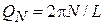и энергия. Поскольку 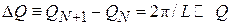, то разрешенная зона имеет квазинепрерывный спектр, обусловленный конечной протяженностью кристалла. При 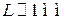расстояние между уровнями .

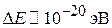Скорость квазичастицы является групповой скоростью волны

.

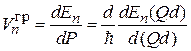Для свободного электрона и групповая скорость 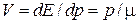совпадает со скоростью частицы. Для квазичастицы из (3.83) получаем

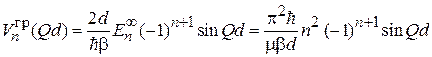. (3.85)

Около края зон возникают стоячие волны, 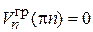и энергия не перемещается по кристаллу. Экстремальная скорость соответствует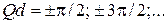

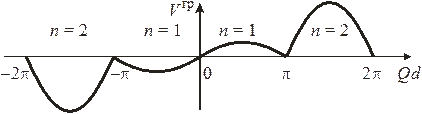
Рис. 3.25. Групповая скорость

Эффективная масса. Инертная масса определяется из второго закона Ньютона

, .

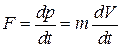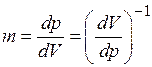Для квазичастицы 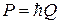и для зоны n находим

.

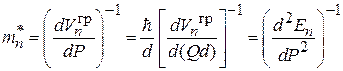Около минимума функции 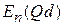эффективная масса положительная, около максимума – отрицательная. Рост функции соответствует положительной массе, убывание – отрицательной. Из (3.85) находим

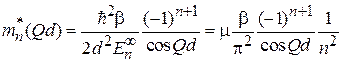. (3.86)

Для первой зоны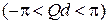

.

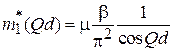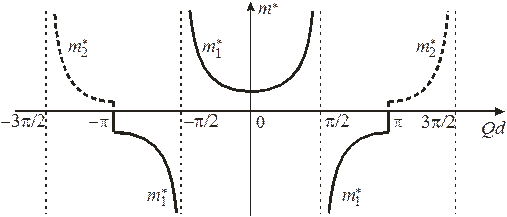
В середине первой зоны

.

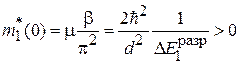Эффективная масса в середине первой зоны обратно пропорциональна ширине зоны. У края зоны

.

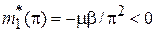Если под действием внешней силы F квазиимпульс электрона увеличивается, приближаясь к границе зоны, то резко усиливается отраженная волна. Импульс, приходящий к электрону от решетки, направлен против F и имеет большую величину, поэтому ускорение направлено против силы и масса квазичастицы отрицательная.

Около нижней границы второй зоны | Qd | = π из (3.86) получаем

.

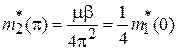Если внешняя сила увеличивает квазиимпульс и электрон удаляется от нижней границы второй зоны, то отраженная от решетки и идущая навстречу волна ослабевает, и электрон получает дополнительное ускорение в сторону силы. Поэтому масса квазичастицы положительная и меньшая . При высокой проницаемости барьера 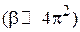эффективная масса гораздо меньше массы свободного электрона.

Метод эффективной массы рассматривает электрон кристалла во внешнем поле 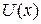как квазичастицу с эффективной массой m * в поле 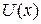. Определениям

,

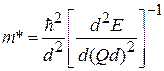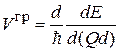
соответствует дисперсионное соотношение

.

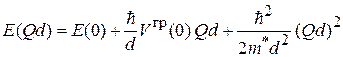В середине первой зоны 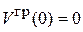. Выбираем начало отсчета энергии 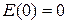и получаем зависимость 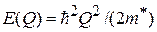для свободного движения – для квазичастицы нет поля кристалла. В середине зоны Бриллюэна квазичастица описывается эффективной массой m*, импульсом 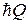и гамильтонианом 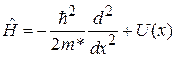. Стационарное уравнение Шредингера имеет вид

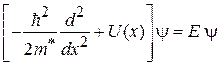. (3.87)

Date: 2015-05-19; view: 789; Нарушение авторских прав