Локализация Андерсона

Примесный атом. В периодическом поле кристалла электрон с энергией в разрешенной зоне, описывается волной Блоха и рассматривается как свободная квазичастица, обнаруживаемая в любом месте кристалла. Примесный атом нарушает периодичность кристалла, происходит захват электрона атомом. Энергия электрона оказывается в запрещенной зоне. Явление описал Филипп Уорен Андерсон в 1958 г.

Спектральное уравнение. Примесный атом внедрения в точке x ₀ кристалла дает вклад в потенциальную энергию электрона 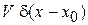. Уравнение Шредингера получает вид

, (3.88)

где 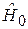– гамильтониан электрона в невозмущенной решетке конечного размера. Решение разлагаем по базису N невозмущенных функций дискретного спектра разрешенной зоны

. (3.89)

Невозмущенные функции удовлетворяют

.

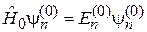Подставляем (3.89) в (3.88) и получаем одно уравнение с N + 1 неизвестными

.

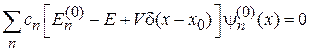Найдем возможные значения энергии E. Умножаем уравнение на 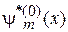, интегрируем по объему кристалла и используем:

1) Ортонормированность базиса

;

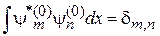2) Фильтрующее свойство дельта-функции

;

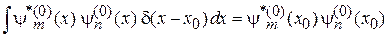3) Фильтрующее свойство символа Кронекера.

Получаем

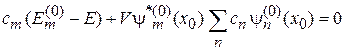. (3.90)

Согласно (3.89) сумма равна 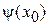. Из (3.90) находим

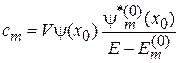. (3.91)

Подстановка и 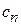в (3.90) дает

.

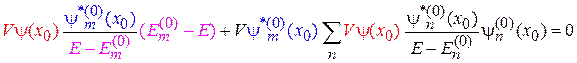Составляющие, показанные одинаковым цветом, сокращаются. В результате

.

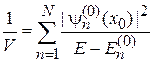Приводим сумму к общему знаменателю и получаем алгебраическое уравнение для энергии электрона Е

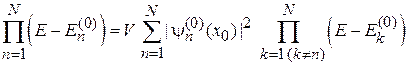. (3.92)

Анализ уравнения. Неизвестная имеет степень N, поэтому уравнение имеет N решений для энергий возмущенных уровней.

В левой стороне находится полином по Е степени N, в правой – степени (N – 1).

При 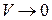правая сторона (3.92) равна нулю. В левой стороне энергия принимает одно из невозмущенных значений 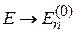. При слабом возмущении спектр не изменяется.

При сильном возмущении в виде отталкивания 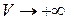, или притяжения 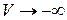энергия 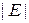растет. В левой стороне (3.92) главный вклад дает наибольшая степень 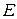, тогда для одного из решений получаем 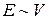. Остальные 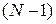решений конечные. Если левая сторона (3.92) конечная, а справа V неограниченно растет, то его сомножитель должен стремиться к нулю. Получаем уравнение степени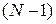

.

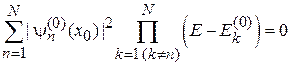В результате 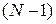решений для 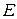близки корням невозмущенного уравнения. При локальном возмущении кристаллической решетки один уровень разрешенной зоны отщепляется и при 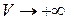поднимается вверх, при 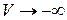опускается вниз. В запрещенной зоне появляется состояние y_л. Остальные уровни практически не меняют своего положения.

Состояние в запрещенной зоне разлагаем в ряд по базису 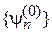невозмущенных функций дискретного спектра разрешенной зоны

.

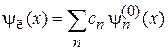Коэффициенты находим из (3.91)

,

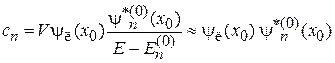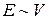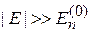где учтено и при 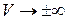. Подстановка коэффициентов в разложение дает

,

где использована полнота базиса 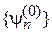в виде

.

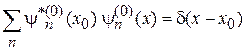Следовательно, при сильном возмущении электрон в запрещенной зоне локализован в области возмущения 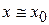. Чем слабее возмущение, тем ближе энергия электрона к разрешенной зоне и больше область локализации. При 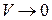локализованное состояние переходит в нелокализованное состояние разрешенной зоны, обнаруживаемое в любом месте кристалла.

Date: 2015-05-19; view: 501; Нарушение авторских прав