ПРИМЕРЫ. 1.Автоэлектронная эмиссия – прохождение электрона с энергией Е из металла в вакуум под действием внешнего электрического поля напряженностью E

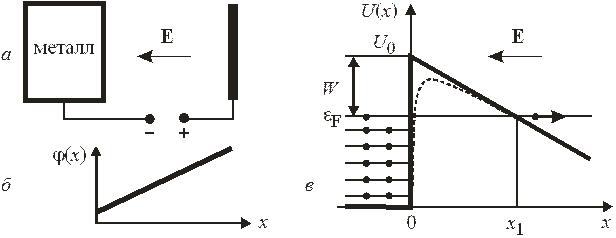
1. Автоэлектронная эмиссия – прохождение электрона с энергией Е из металла в вакуум под действием внешнего электрического поля напряженностью E.

При образовании кристаллической решетки простого металла (элементы таблицы Менделеева с электронами на s - и p -оболочках) слабосвязанные валентные электроны отрываются от атомов, становятся свободными и при низкой температуре имеют полную энергию 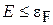, где 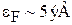– энергия Ферми типичного металла. При низкой температуре длина свободного пробега электрона ~ 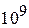межатомных расстояний, или около 1 см. На границе металл–вакуум на электрон действуют возвращающие силы со стороны нескомпенсированных положительных ионов решетки и электронного облака, окружающего металл. Объем металла для электрона является потенциальной ямой с работой выхода 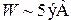. Тепловая энергия 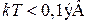активизирует электроны лишь вблизи уровня Ферми и основная масса электронов не может покинуть металл. Если электрическое поле направить к металлу, то график потенциальной энергии наклоняется. Ширина потенциального барьера становится конечной и происходит туннельный эффект, называемый холодная или автоэлектронная эмиссия. Явление обнаружил Роберт Вуд в 1897 г., исследовали Ральф Фаулер и Лотар Нордгейм в 1928 г.

Однородное поле создает при 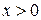распределения потенциала

.

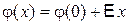Потенциальной энергии электрона

.

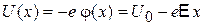Протяженность барьера на уровне Ферми получаем из условия

,

тогда

.

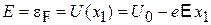Вводим работу выхода

,

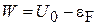находим

.

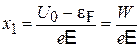Из (3.73)

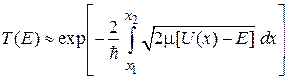
получаем

,

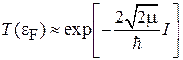где

.

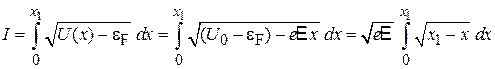Заменяем и находим

,

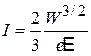коэффициент прохождения

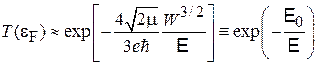, (П.4.1)

где эффективное задерживающее поле

.

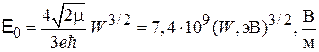Плотность потока электронов, подходящих из объема к поверхности металла при температуре T:

,

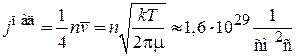где 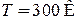; 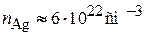. Плотность электрического тока автоэлектронная эмиссия серебра

.

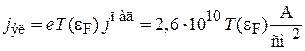Приведенный на рисунке сплошной линией график потенциальной энергии не учитывает поляризацию электроном металлической поверхности, от которой он находится на расстоянии x. Изображение электрона имеет заряд 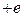, располагается на расстоянии x за поверхностью металла и действует на электрон с силой притяжения 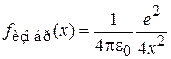, создающей потенциальную энергию

.

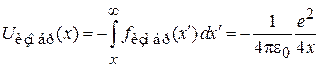Результирующая потенциальная энергия

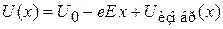
показана на рисунке пунктирной линией. Ее учет уменьшает работу выхода W.

Автоэлектронная эмиссия используется в электронных микроскопах, рентгеновских трубках, приемниках инфракрасного излучения.

2. Рассеяние на ступенчатом барьере. Найти коэффициент прохождения барьера 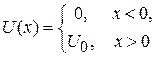частицей с энергией 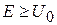. Рассмотреть рассеяние в прямом и обратном направлениях.

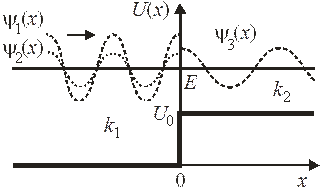
На оси x графика 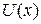выделяем область 1 при и область 2 при 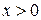. Для каждой области используем стационарное уравнение Шредингера

,

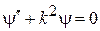где

.

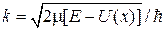Используем общее решение

.

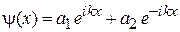При падении частицы на барьер с левой стороны получаем частные решения в виде падающей, отраженной и проходящей волн

,

, ,

, .

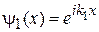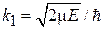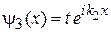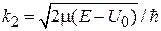Граничные условия (3.11) и (3.12) при 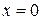имеют вид

,

,

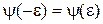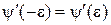где 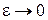, и дают

,

.

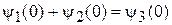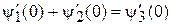Подставляем решения и получаем

,

.

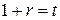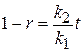Из системы уравнений находим амплитуды волн

,

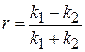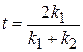, (П.4.2)

и коэффициент отражения

.

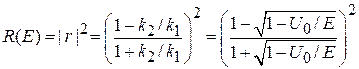Коэффициент прохождения получаем из условия унитарности (3.72)

.

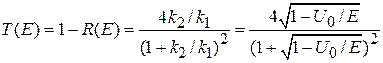Частные случаи:

При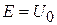

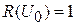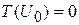, – полное отражение.

При 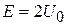находим

.

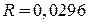При 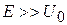разлагаем решение в ряд по аргументу 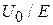и получаем

.

Обращение движения соответствует замене

,

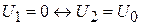тогда

.

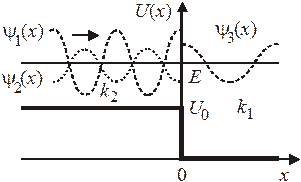
Из (П.4.2) получаем

,

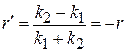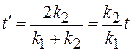. (П.4.3)

Функции R (E) и T (E) не изменяются. Обращение движения частицы через барьер не изменяет коэффицинты отражения и прохождения. Это следует из инвариантности уравнения Шредингера при обращении времени, означающей равенство вероятностей взаимообратимых процессов.

Независимость коэффициента отражения от направления движения парадоксальна с точки зрения классической физики. Действующая на частицу сила при 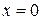направлена в сторону уменьшения потенциальной энергии – влево на первом рисунке и вправо на втором, а частица в обоих случаях отражается влево. Классическая физика в данном случае не применима, поскольку квазиклассическое приближение не дает правильного результата при малой ширине скачка потенциала по сравнению с длиной волны де Бройля.

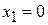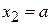3. Рассеяние на локальных барьерах. Частица с волновым числом k проходит через барьеры 1 и 2 сосредоточенные при и . Амплитуду прохождения системы барьеров t выразить через амплитуды прохождения 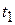, 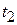и отражения 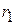, 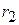каждого из барьеров по отдельности.

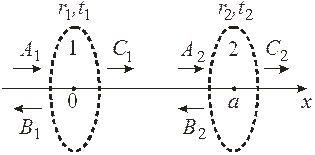
Используем амплитуды бегущих волн 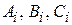около барьера 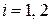. Фиксируем 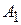и 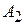, тогда для локальных барьеров

,

,

,

.

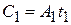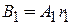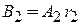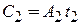Для системы барьеров

,

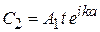где учтено, что при перемещении волны между входом и выходом набегает фаза .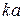

Волна 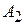в промежутке между барьерами складывается из волны 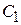и волны 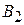, отразившейся от барьера 1, тогда

,

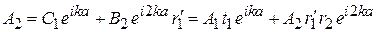где учены изменения фаз волн на пути между барьерами и амплитуда отражения 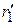волны 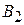от барьера 1. Из последнего уравнения находим

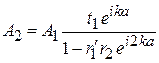
и получаем

,

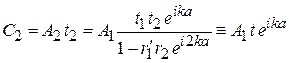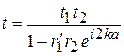. (П.4.4)

Для комплексного числа 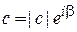используем

,

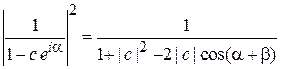и полагаем

, , .

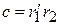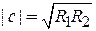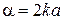Находим коэффициент прохождения

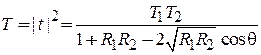, (П.4.4а)

где

; ;

;

;

.

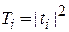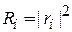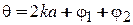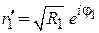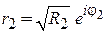Для симметричной системы барьеров

,

,

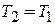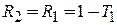из (П.4.4а) находим

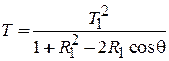. (П.4.4б)

Если энергия частицы удовлетворяет условию резонанса

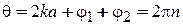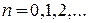, , (П.4.4в)

то 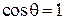, , 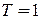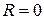и система барьеров не отражает частицу при любом .

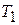Вдали от резонанса при 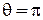из (П.4.4а) получаем

.

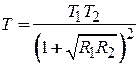При малой проницаемости барьеров 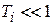, 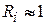находим

.

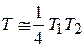4. Рассеяние на прямоугольном барьере. Для частицы с энергией 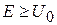найти коэффициент прохождения барьера 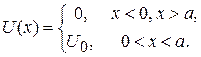Получить условие отсутствия отражения. Рассмотреть туннельный эффект при 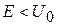, и перевернутый барьер. Система реализуется на практике при контакте двух металлов, разделенных диэлектриком или полупроводником.

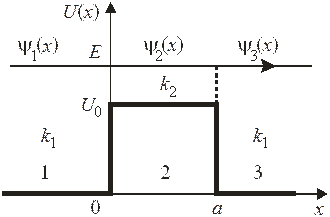
Стандартное решение. Выделяем области 1, 2 и 3. Из уравнения Шредингера

,

для областей 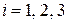получаем

, ,

, ,

.

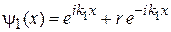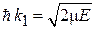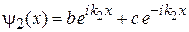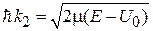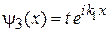Имеем неизвестные параметры: r, t, a, b. Используем условия сшивания

,

,

,

.

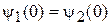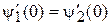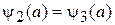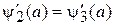Получаем систему алгебраических уравнений

,

,

,

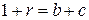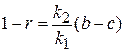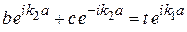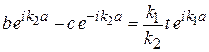
Решив их и вычислив t, найдем

.

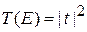Вычисления громоздкие. Рассмотрим другой путь.

Решение на основе системы барьеров. Барьер рассматриваем как состоящий из двух ступенчатых барьеров с амплитудами прохождения и отражения для левого барьера (П.4.2)

, ,

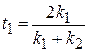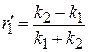для правого барьера (П.4.3)

, .

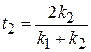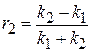Для системы барьеров используем (П.4.4)

.

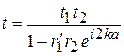Подстановка дает

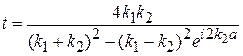. (П.4.5)

Используем

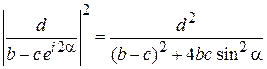
с вещественными

, , , .

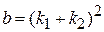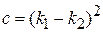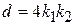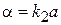Находим коэффициент прохождения

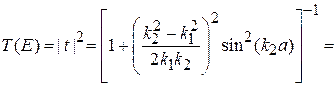
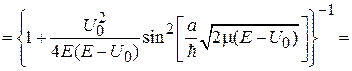
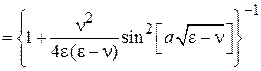. (П.4.6)

Параметры ε и ν в единицах 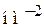описывают энергию частицы и высоту барьера, выраженные в электрон-вольтах:

;

.

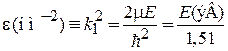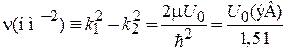При 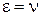энергия частицы равна высоте барьера, и из (П.4.6) получаем

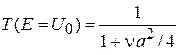. (П.4.6а)

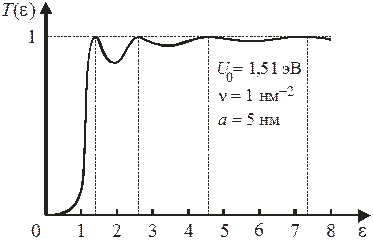
На рисунке показана зависимость коэффициента прохождения от энергии частицы для барьера шириной 5 нм, высотой 1,51 эВ.

Частные случаи:

При 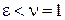, 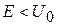имеем 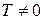– туннельный эффект.

При 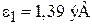, , 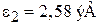,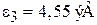... функция синус равна нулю, получаем 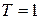– резонансное прохождение без отражения.

Резонансное прохождение. Частица с энергией 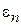не отражается при

.

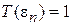Из (П.4.6)

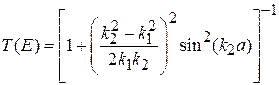
получаем

,

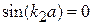тогда

, ,

,

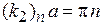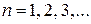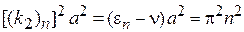длина волны де Бройля 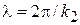удовлетворяет условию

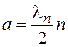(П.4.6б)

– в пределах барьера укладывается целое число полуволн и возникает квазисвязанное состояние с энергией

.

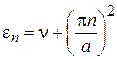Падающая волна проходит ширину барьера и набирает ход 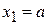, часть волны в результате отражений проходит путь три раза и набирает ход 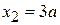. Волны интерферируют с разностью хода 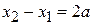. Если длина волны де Бройля электрона удовлетворяет условию максимума интерференции 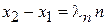, где 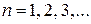, то выполняется (П.4.6б), и волны усиливаются. Образуется квазисвязанное состояние и частица задерживается в области барьера. Она делает неограниченное число попыток пройти барьер и достигается 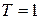. В оптике прохождение барьера без ослабления света называется просветлением оптики.

Туннельный эффект происходит при .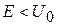

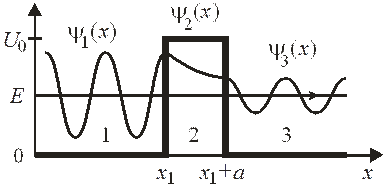
Уравнение Шредингера для областей 1, 2, 3 дает

, ,

,

;

, ,

.

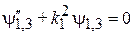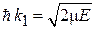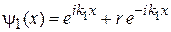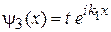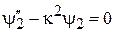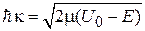Коэффициент прохождения ищем, используя (П.4.6):

.

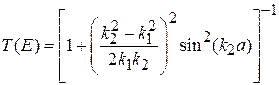Сравниваем

, ,

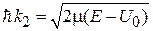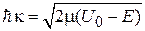получаем

.

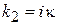Учитываем

,

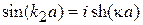где использовано

, .

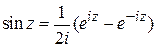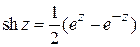Находим

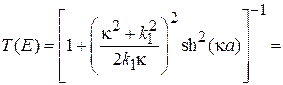
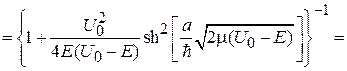
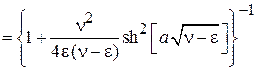, (П.4.7)

где

;

.

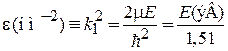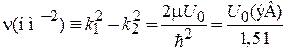Для сильного барьера 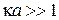с учетом

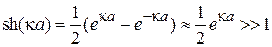
из (П.4.7) получаем

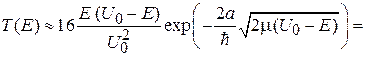
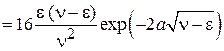. (П.4.8)

Выражение (П.4.8) согласуется с квазиклассическим результатом (3.73а)

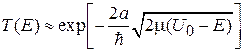
с точностью до множителя перед экспонентой.

Рассеяние на прямоугольной яме.

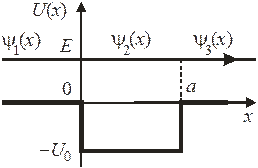
Используем (П.4.6) с заменой 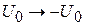, получаем

.

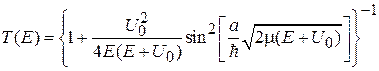Date: 2015-05-19; view: 729; Нарушение авторских прав