Электрон в периодической структуре. Имеются N одинаковых потенциальных ям, в которых на некотором уровне может находиться электрон

Имеются N одинаковых потенциальных ям, в которых на некотором уровне может находиться электрон. Ямы образуют периодическую структуру. При сближении ям возникает туннельное перемещение электрона между ямами. Это приводит к расщеплению уровня одиночной ямы на N подуровней. Множество подуровней называется зоной – областью с характерными свойствами, например, зона проводимости, валентная зона. Основы зонной теории кристалла заложили Феликс Блох и Леон Бриллюэн в 1928 г. и Рудольф Пайерлс в 1930 г. Задачу о движении электрона в периодическом поле потенциальных ям или барьеров, моделирующих кристаллическую решетку, рассмотрели Ральф Крониг и Вильям Пенни в 1931 г. Электрон в поле кристалле описывается как квазичастица. В отличие от электрона, на который действуют силы со стороны узлов решетки, для квазичастицы решетка не существует, она движется с групповой скоростью, квазиволновым числом и квазиимпульсом и имеет эффективную массу, отличающуюся от массы свободного электрона. На квазичастицу действует только внешнее поле по отношению к решетке. Влияние кристалла учитывается эффективной массой.

Расщепление уровня при сближении ям. Рассмотрим две δ-образные ямы в точках 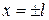с потенциальными энергиями

,

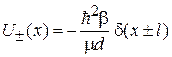где 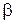– борновский параметр, d – параметр с размерностью длины. Для одиночной ямы существует единственное связанное состояние (П.3.15) частицы

,

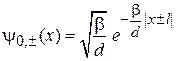где 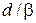– расстояние, на котором существенно убывает волновая функция. Энергия частицы (П.3.16)

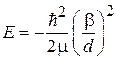
не зависит от положения ямы.

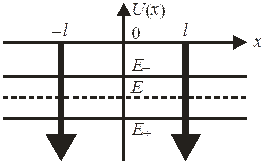
Две ямы 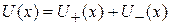образуют симметричную систему 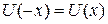, поэтому существуют линейно независимые четное 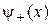и нечетное 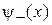состояния. При большом расстоянии между ямами

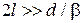
пренебрегаем влиянием соседней ямы на волновую функцию. Для системы ям получаем четную и нечетную суперпозиции

.

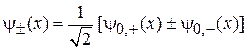Ищем энергии состояний

.

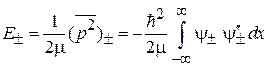Интегрирование по участкам 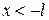, 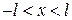и 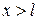с разными подынтегральными функциями дает

.

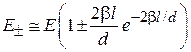Экспоненциальный множитель описывает туннельный переход частицы между ямами. Уровень 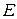одиночной ямы расщепляется на уровень четного состояния 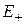и уровень нечетного состояния 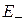, причем

.

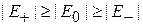Четный уровень находится ниже нечетного и является основным состоянием. Степень расщепления уровней

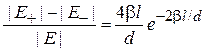
возрастает при сближении ям. Благодаря туннельному эффекту частица с течением времени периодически переходит между ямами с периодом

.

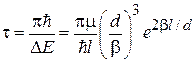Полученные результаты верны и для большого числа ям.

Одномерная решетка имеет периодически расположенные узлы, являющиеся потенциальными ямами или барьерами для электрона. Рассмотрим неограниченную δ-образную решетку барьеров

,

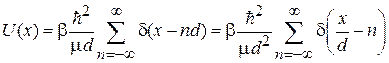где d – постоянная решетки; m – масса свободного электрона; β – безразмерный параметр, определяющий силу барьера; 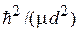– имеет размерность энергии.

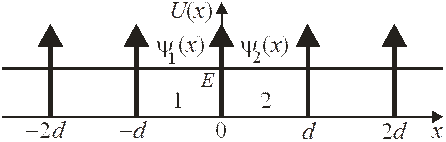
Состояние электрона в решетке получим из уравнения Шредингера (3.1)

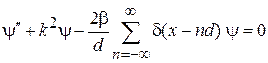, (3.75)

где 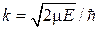– волновое число, и условия сшивания функций для соседних периодов решетки. Вне точечных барьеров при 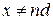уравнение (3.75) имеет вид

.

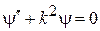На участке 2 при 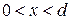используем общее решение в виде бегущих в противоположные стороны волн

.

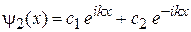Найдем связь между состояниями для соседних интервалов.

Волна Блоха. Электрон, движущийся в направлении оси x, описываем волной 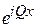с квазиволновым числом Q и с модулированной амплитудой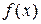

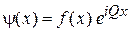. (3.76)

Решетка периодическая, уравнение Шредингера не изменяется при замене

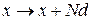, N – целое число,

тогда модулирующая функция также периодическая

.

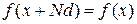В результате замена 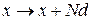в (3.76) дает

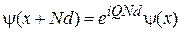, (3.77)

.

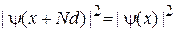Электрон обнаруживается в пределах каждого периода решетки с одинаковым распределением вероятности. Это следует из равноправия всех периодов для неограниченной решетки.

Волновые функции соседних интервалов. В (3.77) полагаем 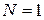, 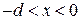и находим соотношение между функциями на интервалах 1 и 2

, ,

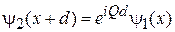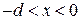тогда

.

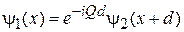С учетом

,

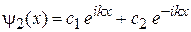получаем

.

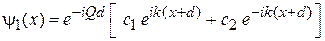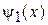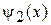Дисперсионное соотношение. Сшиваем и при 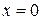. Условие (3.11) непрерывности функций

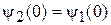
дает

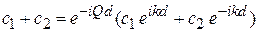. (3.77а)

Условие (3.13) с δ-потенциалом

, ,

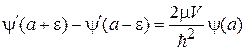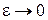с учетом

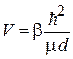
получает вид

.

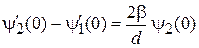Подстановка функций дает уравнение

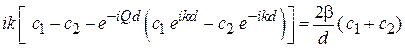. (3.77б)

Получаем систему однородных уравнений (3.77а) и (3.77б) для неизвестных Q, 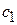и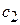

,

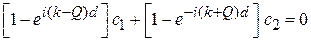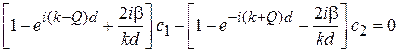. (3.78)

Найдем квазиволновое число Q из условия совместности системы уравнений. Определитель коэффициентов приравниваем к нулю и получаем дисперсионное соотношение

, (3.79)

связывающее квазиволновое число Q и волновое число

.

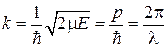Дисперсия от лат. dispersio – разброс. Соотношение (3.79) ограничивает допустимые значения волнового числа и энергии электрона в решетке, позволяет выразить энергию через квазиволновое число.

Date: 2015-05-19; view: 548; Нарушение авторских прав