Квазиклассическое квантование ВКБ. Точное решение уравнения Шредингера возможно для ограниченного числа функций потенциальной энергии

Точное решение уравнения Шредингера возможно для ограниченного числа функций потенциальной энергии. Квазиклассическое квантование является приближенным методом. Фазу волновой функции разлагаем в ряд по степени малости и ограничиваемся первыми двумя слагаемыми. Это допустимо, если длина волны де Бройля частицы гораздо меньше расстояния существенного изменения потенциальной энергии. Метод разработали Г. Вентцель, Х. Крамерс и Л. Бриллюэн в 1926 г.

Уравнение состояния (3.1)

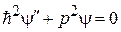, (3.51)

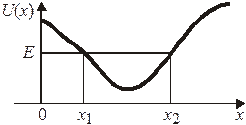
где 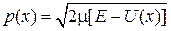– импульс частицы c энергией Е в точке x.

При 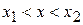решение ищем в виде волны

, (3.52)

где 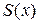– комплексная фазовая функция, 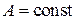. Подставляем (3.52) в (3.51), учитываем

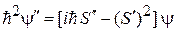
и получаем

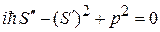. (3.53)

Решаем (3.53), разлагая 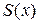в ряд по степеням 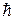и ограничиваясь двумя слагаемыми

.

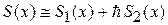Первое приближение. Считаем медленным изменение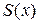

.

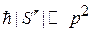Из (3.53) получаем

. (3.54)

Интегрирование дает

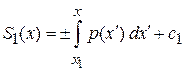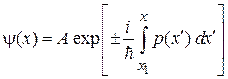, . (3.55)

Фаза волновой функции определяется интегралом от импульса по пути между точкой поворота и текущим положением частицы – условие квантования Бора–Зоммерфельда.

Условие применимости решения. Учитывая (3.54) , и используя

, , ,

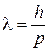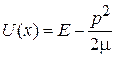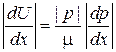из 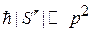получаем

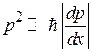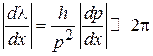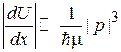, , . (3.56)

Согласно (3.56) 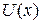изменяется медленно. Разлагаем ее в ряд Тейлора около точки поворота x ₁ и ограничиваемся двумя слагаемыми

,

,

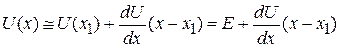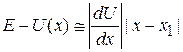где 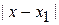– расстояние от точки поворота до области, где применимо (3.56). Используя (3.56), находим

,

.

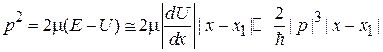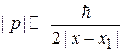Из 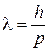и (3.56) получаем

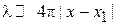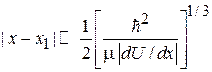, . (3.57)

Квазиклассическое приближение применимо, если длина волны де Бройля гораздо меньше расстояния, на котором существенно изменяется потенциальная энергия. Это соответствует большому импульсу и его малому изменению на протяжении указанного расстояния. Решение ВКБ неприменимо вблизи точки поворота, где

, , .

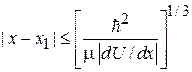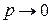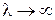Второе приближение. Подставляем в качестве малой поправки в исходное уравнение (3.53)

, .

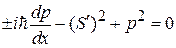Учитываем (3.56) 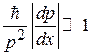, разлагаем скобку в ряд и оставляем первые два слагаемые 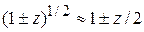, тогда

,

.

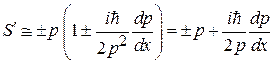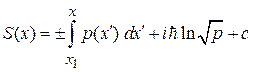Из (3.52) для 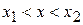находим общее решение

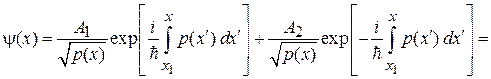
. (3.58)

Плотность вероятности получаем усреднением квадрата высокочастотного множителя 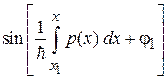в (3.58) по периоду. С учетом находим

.

Множитель связан с тем, что с увеличением скорости уменьшается время пребывания частицы в единичном интервале около рассматриваемой точки. Условие нормировки с учетом 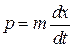, 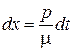дает

, ,

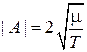где Т – период движения.

Вне классической области 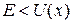, поэтому 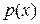– мнимая функция. Оставляя в (3.58) решения, убывающие при удалении от точек поворота, получаем

, (3.60)

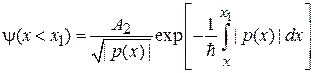. (3.61)

Date: 2015-05-19; view: 615; Нарушение авторских прав