Анализ дисперсионного соотношения

(3.79)

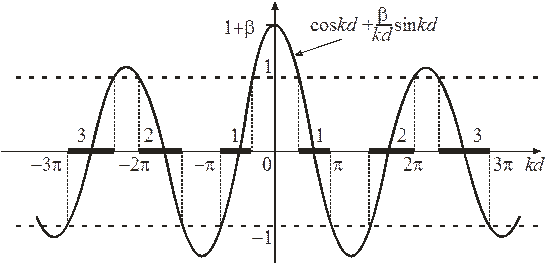
Разрешенные и запрещенные зоны. Правая сторона в виде функции с аргументом kd показана на рисунке сплошной кривой. Левая сторона ограничена 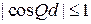интервалом между пунктирными линиями, тогда

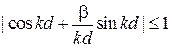. (3.80)

Области значений kd, удовлетворяющие (3.80), называются разрешенными зонами 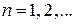, и обозначены на горизонтальной оси отрезками толстых линий. Между ними находятся запрещенные зоны.

Верхняя граница разрешенной зоны. С увеличением k разрешенная зона заканчивается в точке 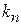при выполнении

, , ,

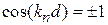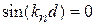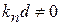тогда

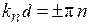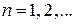, (3.81)

При этом согласно (3.79)

волновое число совпадает с квазиволновым числом

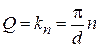. (3.82)

Выражаем (3.81) через длину волны де Бройля 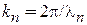, получаем

.

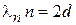Это есть условие максимума отраженной волны Вульфа–Брегга (П.1.2)

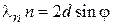
для угла скольжения 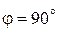, т. е. при нормальном падении на кристалл. У верхней границы разрешенной зоны электрон испытывает брэгговское отражение и не распространяется по кристаллу. Интенсивности падающей 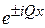и отраженной 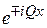волн сравниваются. Их интерференция образует стоячие волны. Найдем их вид.

Если при отражении фаза волны не меняется, то стоячая волна четная

,

.

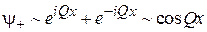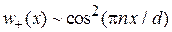При 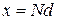, где N – целое, выполняется 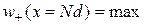, и электроны скапливаются вблизи ионов. Электрическое взаимодействие электрона с ионом

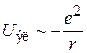
дает вклад в энергию кристалла. При сближении электрона с ионом уменьшается r и энергия кристалла понижается на 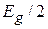по сравнению с равномерным распределением электронов.

Если при отражении фаза волны увеличивается на p, то стоячая волна нечетная

,

,

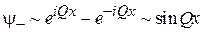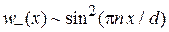электроны скапливаются между ионами, r увеличивается, энергия кристалла повышается на 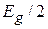. Это состояние принадлежит следующей разрешенной зоне. Между ними находится запрещенная зона шириной .

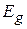Электрон как квазичастица. Электрон характеризуется:

массой m,

волновым числом k,

импульсом ,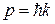

скоростью v.

В кристалле электрон описывается волной Блоха 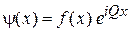. На достаточно больших участках кристалла 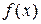усредняется, и бегущую волну 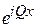рассматриваем как квазичастицу в свободном пространстве и характеризуем:

квазиволновым числом Q,

эффективной массой m*,

квазиимпульсом ,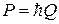

групповой скоростью V.

Если кристалл находится во внешнем поле, то импульс электрона изменяется под действием поля кристалла и внешнего поля. Квазиимпульс изменяется только внешним полем и описание квазичастицы существенно более простое.

Зависимость энергии от квазиволнового числа для частных значений параметра β – степени непроницаемости барьера.

1) Абсолютно свободный электрон соответствует прозрачному барьеру с 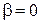. Дисперсионное соотношение

получает вид

,

.

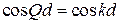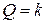Ограничение для k и Q отсутствует, спектр непрерывный (рис. 1)

.

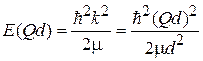Электрон обнаруживается в любой точке решетки с одинаковой вероятностью.

2) Абсолютно связанный электрон соответствует непроницаемому барьеру с 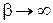. Дисперсионное соотношение

имеет смысл при

, ,

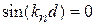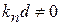тогда

,

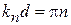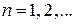
Решетка распадается на ямы шириной d с непроницаемыми стенками, спектр дискретный (рис. 2)

.

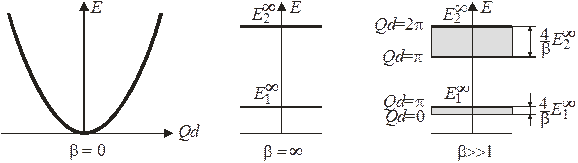
1 2 3

3) Приближение сильной связи. Барьеры сильные, 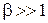, что близко к случаю 2, тогда

, ,

,

.

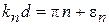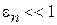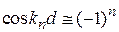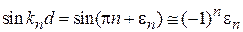Из (3.79)

получаем

,

.

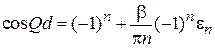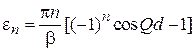Учитывая 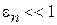, находим

,

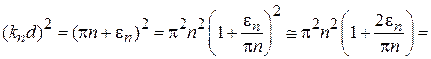
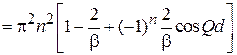где использовано 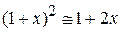при 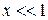. Подстановка в 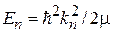дает зависимость энергии частицы в зоне nот квазиволнового числа

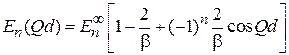, (3.83)

где

.

Энергетические зоны. Согласно (3.82) верхняя граница разрешенной зоны 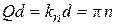. Предыдущая зона заканчивается при 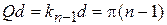. Тогда величина Qd в разрешенной зоне n меняется в пределах

.

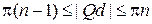Для границ разрешенной зоны получаем энергию из (3.83) с учетом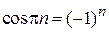

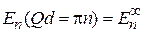– верхняя граница зоны,

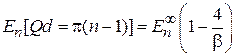– нижняя граница зоны,

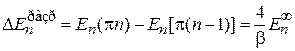– ширина зоны. (3.84)

Чем больше непроницаемость барьера β, тем меньше ширина разрешенной зоны. При 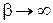ширина зоны равна нулю и получается рассмотренный ранее случай 2.

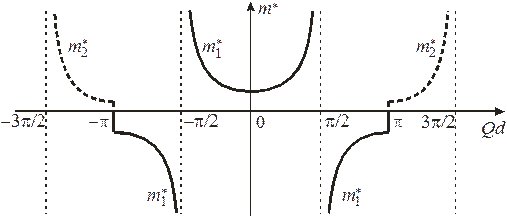
График 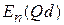для первых двух зон показан на рисунке толстыми сплошными линиями. Верхняя граница зоны 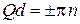касается параболы 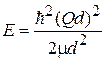(ранее рассмотренный случай 1), показанной пунктиром, где выполняется .

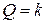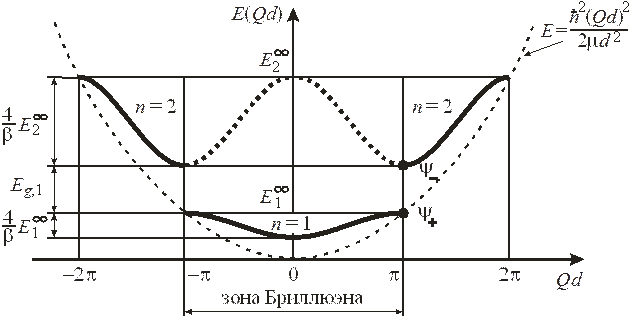
Ширина запрещенной зоны, или энергетической щели:

.

Появление щели объясняется тем, что при 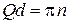возникают два типа стоячих волн – четная ψ₊ и нечетная ψ_–. Уровень, соответствующий исходной бегущей волне, распадается на два уровня, принадлежащих соседним разрешенным зонам.

Первая зона Бриллюэна. С учетом периодичности 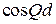замена

, ,

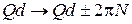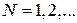не меняет функцию (3.83)

.

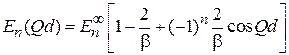Передвигаем левую и правую ветви зоны 2 на ±2π, соответственно. Результат показан толстой пунктирной кривой. Первая и вторая зоны, и аналогично другие зоны, попадают в интервал 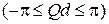, называемый первой зоной Бриллюэна. Квазиволновое число и квазиимпульс достаточно рассматривать в пределах этой зоны. На краю зоны

, .

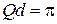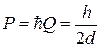При d» 3×10^–8 см энергия края зоны

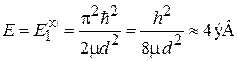
близка к энергии Ферми электронного газа металла.

Конечная протяженность кристалла. Мысленно заменяем кристалла длиной L на множество идентичных соприкасающихся кристаллов. Волновая функция электрона удовлетворяет условию Борна–Кармана (3.8)

.

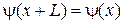На волну Блоха (3.76)

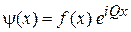
накладываем условие равноправия всех кристаллов 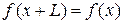и получаем

.

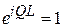В результате

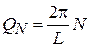, N – целое.

Квазиволновое число квантуется для кристалла конечной протяженности L. При макроскопической протяженности

.

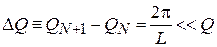Разрешенная зона имеет квазинепрерывный спектр. При 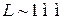расстояние между уровнями .

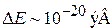Скорость квазичастицы является групповой скоростью волны и равна производная энергии по квазиимпульсу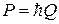

.

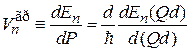Для свободного электрона 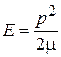и групповая скорость 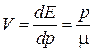совпадает со скоростью частицы. Для квазичастицы используем (3.83)

,

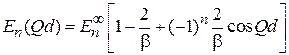получаем

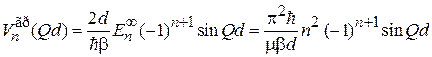. (3.85)

На краю зоны

, , ,

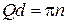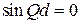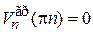бегущая волна полностью отражается от кристаллической плоскости согласно формуле Вульфа–Брэгга, образуется стоячая волна и энергия не перемещается по кристаллу.

В середине разрешенной зоны при 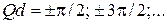скорость достигает максимума.

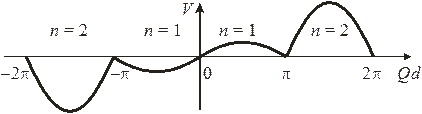
Эффективная масса. Согласно второму закону Ньютона

,

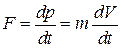инертная масса равна производной импульса по скорости

.

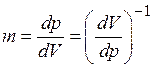Для квазичастицы 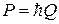в зоне n эффективная масса

,

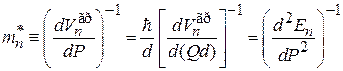где учтено 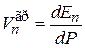. Около минимума функции 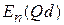эффективная масса положительная, около максимума – отрицательная. Рост функции 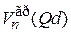соответствует положительной массе, убывание – отрицательной. Используем (3.85)

,

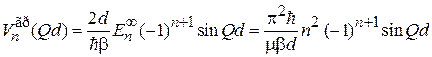находим

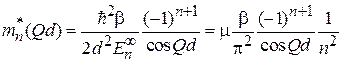. (3.86)

Для первой зоны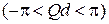

.

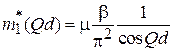В середине первой зоны

,

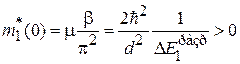где степень непроницаемости барьера β выражена через ширину разрешенной зоны на основании (3.84) 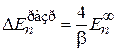. Эффективная масса в середине первой зоны обратно пропорциональна ширине зоны. У края зоны масса отрицательная

.

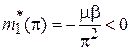Если под действием внешней силы квазиимпульс электрона увеличивается, приближаясь к границе зоны, то резко усиливается отраженная волна. Импульс, приходящий к электрону от решетки, направлен против силы и имеет большую величину, поэтому ускорение направлено против силы и масса квазичастицы отрицательная.

Около нижней границы второй зоны | Qd | = π из (3.86) получаем

.

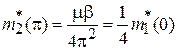Если внешняя сила увеличивает квазиимпульс и электрон удаляется от нижней границы второй зоны, то отраженная от решетки и идущая навстречу волна ослабевает, и электрон получает дополнительное ускорение в сторону силы. Поэтому масса квазичастицы положительная и меньшая 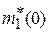. При высокой проницаемости барьера 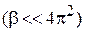эффективная масса гораздо меньше массы свободного электрона.

Метод эффективной массы рассматривает электрон в кристалле и во внешнем поле 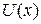как квазичастицу с эффективной массой m * в поле 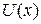. Решетка кристалла учитывается через эффективную массу квазичастицы. Используем определения

,

.

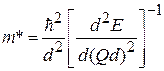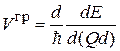При малом 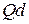, т. е. около середины первой зоны, функцию энергии разлагаем в ряд Маклорена и оставляем первые три слагаемые. Получаем дисперсионное соотношение

.

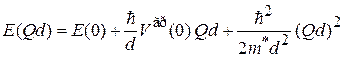Учитываем 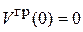, выбираем начало отсчета энергии 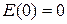и получаем соотношение между энергией и импульсом

,

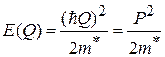совпадающее с выражением для свободной частицы. Следовательно, для квазичастицы нет поля кристалла. В середине зоны Бриллюэна квазичастица описывается постоянной эффективной массой m*, импульсом 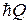и гамильтонианом

.

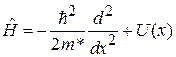Стационарное уравнение Шредингера 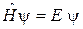во внешнем поле 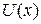имеет вид

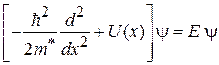. (3.87)

Рассмотрим отклонение от идеального кристалла, вызванное примесным атомом внедрения.

Date: 2015-05-19; view: 629; Нарушение авторских прав