Туннельный эффект

Если полная энергия частицы меньше потенциальной энергии барьера , то классическая частица не проходит через барьер. В квантовой механике частица имеет вероятность пройти такой барьер. Явление называется туннельным эффектом. Его описал Георгий Антонович Гамов в 1928 г. и объяснил парадокс, связанный с α-распадом ядра урана

.

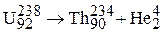Два протона и два нейтрона урана объединяются и образуют α-частицу с энергией 4,18 МэВ. Задерживающий потенциал ядра урана составляет 8,57 МэВ. Тем не менее, α-частица вылетает из ядра благодаря туннельному эффекту и ядро распадается за время . Причина распада в том, что волновая функция не равна нулю в области не доступной для классической частицы. Термин туннельный эффект ввел Вальтер Шоттки в 1931 г.

Туннельный эффект лежит в основе множества явлений квантовой механики. На его основе разработан туннельный микроскоп и туннельный транзистор.

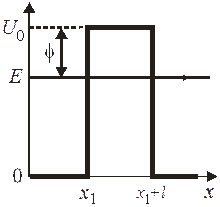
Движение частицы через барьер. Частица с энергией Е в виде бегущей волны

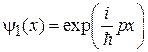
распространяется вдоль оси x и встречает барьер 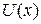, превышающий ее полную энергию:

,

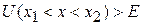где и 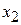– точки остановки классической частицы.

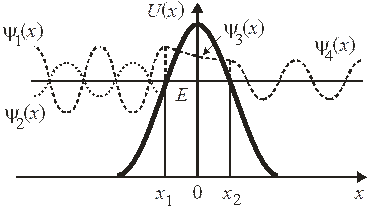
Возникает отраженная волна

.

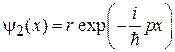Внутри барьера используем квазиклассическое приближение (3.60) в виде затухающей волны

.

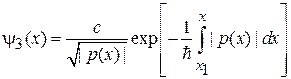За барьером возникает бегущая волна

.

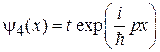Коэффициент прохождения барьера получаем из (3.68)

.

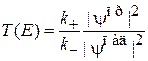При 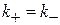находим

,

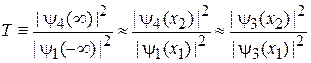где учтены условия сшивания (3.11) при условии малости отраженной волны

, .

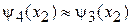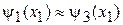Используем

,

,

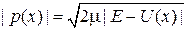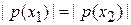из

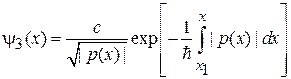
получаем

,

.

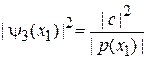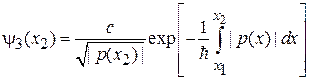С точностью до слабо меняющегося и близкого к единице предэкспоненциального множителя из 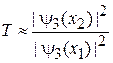находим

. (3.73)

Для прямоугольного барьера шириной 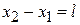и высотой 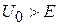из (3.73) получаем

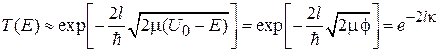, (3.73а)

где – преодолеваемая высота барьера; 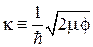. Проницаемость барьера существенна при 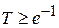, тогда 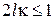, и это ограничивает ширину барьера

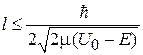. (3.74)

Чем меньше масса частицы, тем более широкий и высокий барьер она преодолевает. Коэффициенты прохождения электрона и протона с одинаковой энергией через один и тот же барьер согласно (3.73а) отличаются в 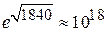раза. Для макроскопического тела туннельный эффект не проявляется.

Объяснение туннельного эффекта. Используем соотношение неопределенностей

.

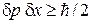Если частица обнаруживается внутри барьера шириной l, то 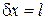, и частица получаем неопределенность импульса

.

Это дает дополнительную кинетическую энергию

.

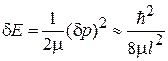Суммарная энергия

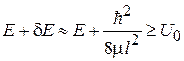
обеспечивает преодоление барьера шириной (3.74).

Сканирующий туннельный микроскоп (СТМ) измеряет микрорельеф проводящей поверхности с помощью туннельного эффекта. Игла из платины, вольфрама или иридия с атомарным острием подводится к поверхности сначала двигателем грубого перемещения, затем пьезосканером на расстояние ≤ 1 нм, которое контролируется по величине туннельного тока. На иглу подается потенциал (0,01–10) В по отношению к поверхности. Туннельный ток I через вакуумный промежуток размером l пропорционален коэффициенту прохождения (3.73а)

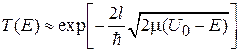
и экспоненциально зависит от l. При 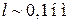ток 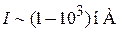. Перемещение иглы на 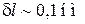меняет ток в 10 раз. Игла периодически сканирует поверхность. Ток поддерживается на одном уровне за счет перемещения иглы перпендикулярно поверхности. Регистрируемые перемещения иглы дают рельеф поверхности. Разрешение по нормали к поверхности достигает 0,005 нм, в плоскости – 0,2 нм, что делает возможным наблюдение отдельных атомов. Атом водорода в основном состоянии имеет размер ~ 0,1 нм. Малая величина используемого потенциала не разрушает исследуемый объект. Изображение в СТМ зависит от рельефа поверхности и от поверхностной плотности состояний образца. СТМ работает при нормальной температуре на воздухе и требует изоляции от вибраций. СТМ разработали в 1981 г. Герд Биннинг (на фото слева) и Генрих Рорер (справа). На фото перед ними находится СТМ. Нобелевская премия 1986 г.

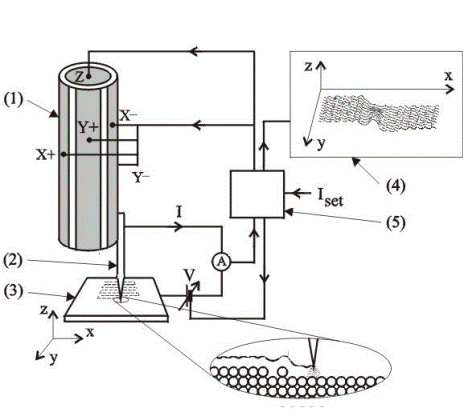
1– пьезо-сканер; 2 – игла; 3 – исследуемый образец; 4 – изображение на дисплее; 5 – электронное управление.

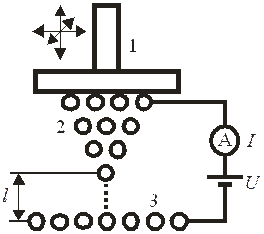
Поверхность Si(111)

(размытость изображения вызвана тепловыми флуктуациями)

Поверхность Cu(111)

Игла СТМ позволяет измерить потенциал точки поверхности проводника со сложной структурой и протекающим током.

Распределение тока, протекающего между двумя контактами в плоскости двумерного проводника, можно получить при помощи СТМ. Отрицательный потенциал иглы, касающейся проводника в точке 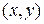, рассеивает упорядоченно движущиеся электроны, и проводимость проводника 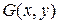уменьшается тем сильнее, чем больше плотность тока в изучаемой точке. Распределение изменений проводимости , где 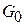– проводимость без касания иглы, дает распределение тока по проводнику. Метод предложен M.A. Topinca et al. Science 289, 2323 (2000).

При помощи СТМ можно измерить энергетическую плотность состояний поверхности проводника путем вариации приложенного к игле напряжения.

Date: 2015-05-19; view: 878; Нарушение авторских прав