Потенциальная яма

Если потенциальная энергия 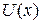имеет минимум, меньший значений при 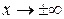, которые считаем одинаковыми и равными нулю, то это потенциальная яма. При 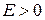движение частицы не ограничено, ее энергия имеет непрерывный спектр, яма лишь рассеивает частицу. При 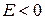частица захвачена ямой, состояние связанное.

Свойства связанных состояний. При 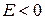частица находится в ограниченных пределах, спектр дискретный 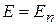, где 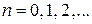– номер состояния. Состояние с наименьшей энергией E ₀ называется основным, остальные – возбужденные. Функции состояний дискретного спектра можно выбрать вещественными.

У края пологой ямы в области, где 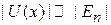, из (3.1) 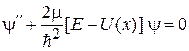для состояния n получаем

, .

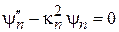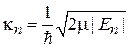Физическое решение убывает при 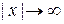и имеет вид

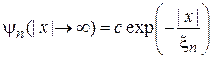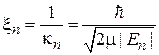, . (3.17)

Частица обнаруживается за пределами ямы в области порядка 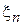благодаря туннельному эффекту.

Для симметричной ямы

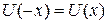
уравнение (3.1) не изменяется при замене 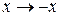. Множество общих решений распадается на линейно независимые и взаимно ортогональные подмножества четных и нечетных вещественных решений

, ,

, .

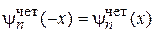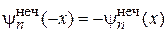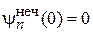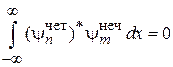Число нулей волновой функции является номером состояния и называется главным квантовым числом 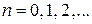Оно определяет длину волны 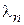, импульс 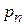и полную энергию частицы. С ростом n уменьшается 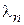, увеличиваются 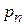и .

Между двумя последовательными нулями функции состояния существует нуль соседнего по энергии состояния.

Спектр состояний одномерной ямы невырожденный – состояния с разными волновыми функциями имеют разные энергии.

Множество связанных состояний 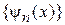образует ортонормированный базис

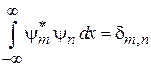. (3.20)

Борновский параметр. В яме с характерной шириной а из соотношения неопределенностей (2.37) получаем характерный импульс частицы 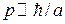и кинетическую энергию 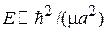. Мера воздействия ямы на частицу определяется параметром

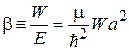, (3.22)

где 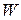– характерной глубина ямы. При 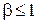яма слабая, при 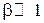яма сильная.

Date: 2015-05-19; view: 488; Нарушение авторских прав