Квазиклассическое квантование ВКБ

Точное аналитическое решение уравнения Шредингера возможно лишь для ограниченного числа функций потенциальной энергии. Для других случаев используются приближенные аналитические и численные методы. Приближенным аналитическим решением является квазиклассическое квантование. Метод разработали Грегор Вентцель, Хендрик Крамерс и Леон Бриллюэн в 1926 г., отсюда название ВКБ.

Метод ВКБ применим, если длина волны де Бройля частицы гораздо меньше расстояния существенного изменения потенциальной энергии. Малая длина волны означает близость к классическому поведению. В отличие от ранее рассмотренной полуклассической квантовой механики, квантование ВКБ дает более точные результаты. Метод применим для частицы, движущейся с большим импульсом в области с плавно изменяющимся потенциалом. Метод не применим к скачкообразным потенциалам и к резонансным явлениям.

Уравнение Шредингера (3.1) для частицы c энергией Е в поле с потенциальной энергией 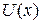записываем в виде

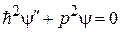, (3.51)

где

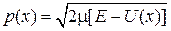
– импульс в точке x. В точках поворота классического движения 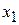и 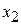частица останавливается,

, , .

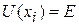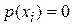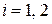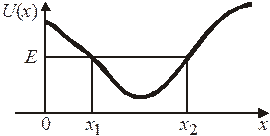
Между точками поворота 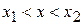кинетическая энергия положительная, импульс вещественный, решение ищем в виде волны

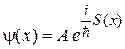, (3.52)

где – фазовая комплексная функция, 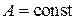– амплитуда. Подставляем (3.52) в (3.51), учитываем

,

,

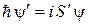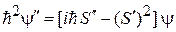получаем точное уравнение для фазовой функции

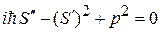. (3.53)

Уравнение нелинейное, решаем его методом последовательных приближений.

Первое приближение. Изменение фазы считаем медленным и не учитываем вторую производную в (3.53)

.

Уравнение (3.53) упрощается

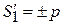. (3.54)

Интегрируем

,

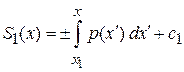находим

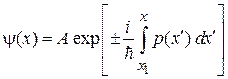. (3.55)

Фаза волновой функции определяется интегралом от импульса по пути между точкой поворота и текущим положением частицы. Результат совпадает с условием квантования Бора–Зоммерфельда полуклассической квантовой теории.

Условие применимости решения (3.55). Из (3.54) 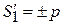получаем модуль отброшенного слагаемого

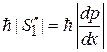. (3.55а)

Для его анализа используем

,

,

,

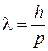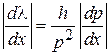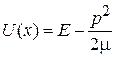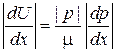. (3.55б)

Использованная медленность изменения фазы

с учетом (3.55а) означает

.

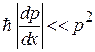Тогда

,

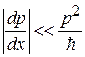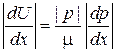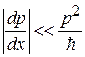– длина волны меняется от точки к точке медленно. Из (3.55б) и получаем

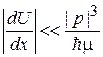(3.56)

– поле 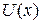изменяется медленно. Поэтому при разложении 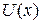в ряд Тейлора около точки поворота x ₁ ограничиваемся первыми двумя слагаемыми

,

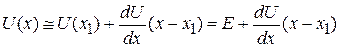, (3.56а)

где 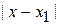– расстояние от точки поворота до области, где применимо (3.56). Используя (3.56а) и (3.56), находим

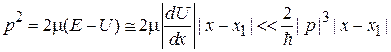. (3.56б)

В неравенстве

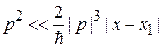
приводим подобные

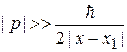. (3.56в)

С учетом

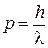
из (3.56в) находим

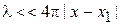(3.57)

– длина волны гораздо меньше расстояния до точки поворота.

Подставляем (3.56в) 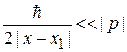в первый элемент строки (3.56б) 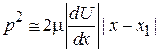, тогда

,

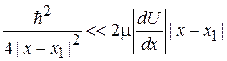приводим подобные

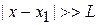, (3.57а)

где

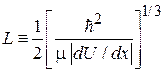
– расстояние, на котором существенно изменяется потенциальная энергия.

Согласно (3.57а) квазиклассическое приближение применимо вдали от точки поворота, когда длина волны де Бройля гораздо меньше расстояния, на котором существенно изменяется потенциальная энергия. Это соответствует большому импульсу и его малому изменению на протяжении указанного расстояния. Решение ВКБ неприменимо вблизи точки поворота при

, , .

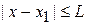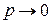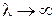Второе приближение. В исходное уравнение (3.53)

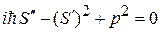
подставляем (3.55а) 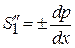и получаем

,

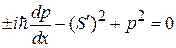тогда

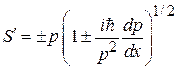. (3.57б)

Учитываем ранее полученное неравенство

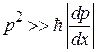
в виде

,

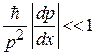Следовательно, второе слагаемое в круглой скобке (3.57б) мало. Разлагаем выражение в ряд по степеням малого параметра и оставляем первые два слагаемые согласно

, ,

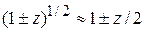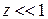тогда

.

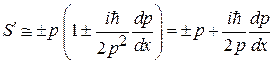Интегрируем

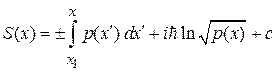, (3.57в)

где использовано

.

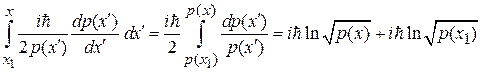Результат

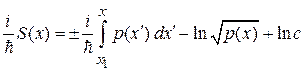
подставляем в (3.52)

,

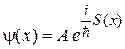получаем общее решение

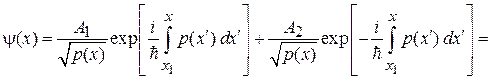
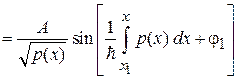. (3.58)

По сравнению с квантованием Бора–Зоммерфельда в (3.58) присутствует множитель 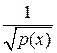. В плотности вероятности

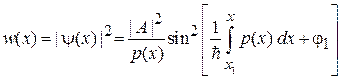
множитель 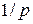связан с тем, что с увеличением скорости уменьшается время пребывания частицы в единичном интервале около рассматриваемой точки.

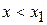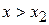Вне классической области при и получаем 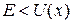и мнимый импульс 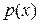. В решении ВКБ (3.58) оставляем функции, убывающие при удалении от точек поворота:

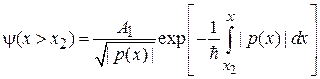, (3.60)

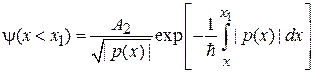. (3.61)

Date: 2015-05-19; view: 577; Нарушение авторских прав