Одномерные стационарные состояния

Одномерные стационарные задачи

Уравнение Шредингера для двухмерных и трехмерных стационарных систем с потенциальной энергией 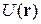сводится в ряде случаев к одномерному уравнению Шредингера (2.59)

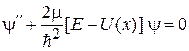, (3.1)

или

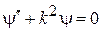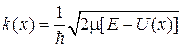, . (3.2)

Общее решение 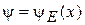содержит полную энергию Е и два свободных параметра. Эти величины находятся из граничных условий и из нормировки волновой функции.

Одномерные стационарные состояния

Переход к одномерной задаче. Трехмерная стационарная система описывается в декартовых координатах уравнением Шредингера (2.57)

.

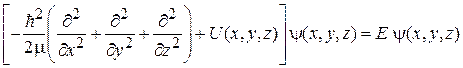Если

,

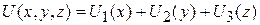то волновая функция факторизуется

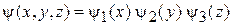
и уравнение распадается на независимые одномерные уравнения

, ,

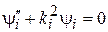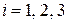где

; .

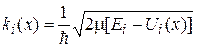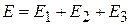Свободная частица. При 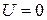уравнение (3.2) имеет общее решение

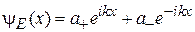, . (3.3)

Волны распространяются по- и против оси x. Если краевые условия не накладываются, то спектр непрерывный .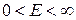

Плотность тока вероятности находим из (2.72)

, ,

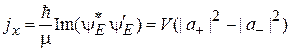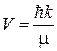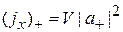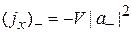, . (3.6)

Задавая плотность электрического тока, получаем 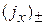, и из (3.6) находим амплитуды волн .

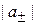Частица в потенциальном ящике. Внутри ящика размером L, где 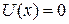, частица с энергией Е описывается функцией (3.3). Учтем стенки ящика. Для этого расширяем определение функции на все пространство, рассматривая систему повторяющихся ящиков, и вводим периодическое условиеБорна–Кармана:

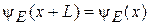. (3.8)

Подстановка (3.3) в (3.8) дает . Учитывая 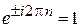, где 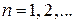, находим, что волновое число, импульс и энергия частицы в ящике квантуются

, , ,

.

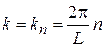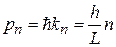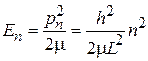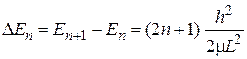Для кристалла с характерным размером 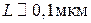получаем расстояние между уровнями 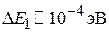. Сравниваем с тепловой энергией частицы газа при нормальной температуре 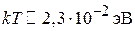. При достаточно высокой температуре и большом ящике спектр энергии квазинепрерывный.

Состояние n занимает в координатном пространстве объем 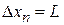, в импульсном пространстве – 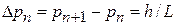, в фазовом пространстве

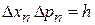. (3.9)

Любое состояние в потенциальном ящике занимает фазовый объем, равный постоянной Планка.

Date: 2015-05-19; view: 496; Нарушение авторских прав