
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лекция 5
|
|
Представление операций симметрии в виде матрицы преобразований

Таблица 1 полное представление и его характеры
| С3v | E | 2С3 | 3sv |
| Г |
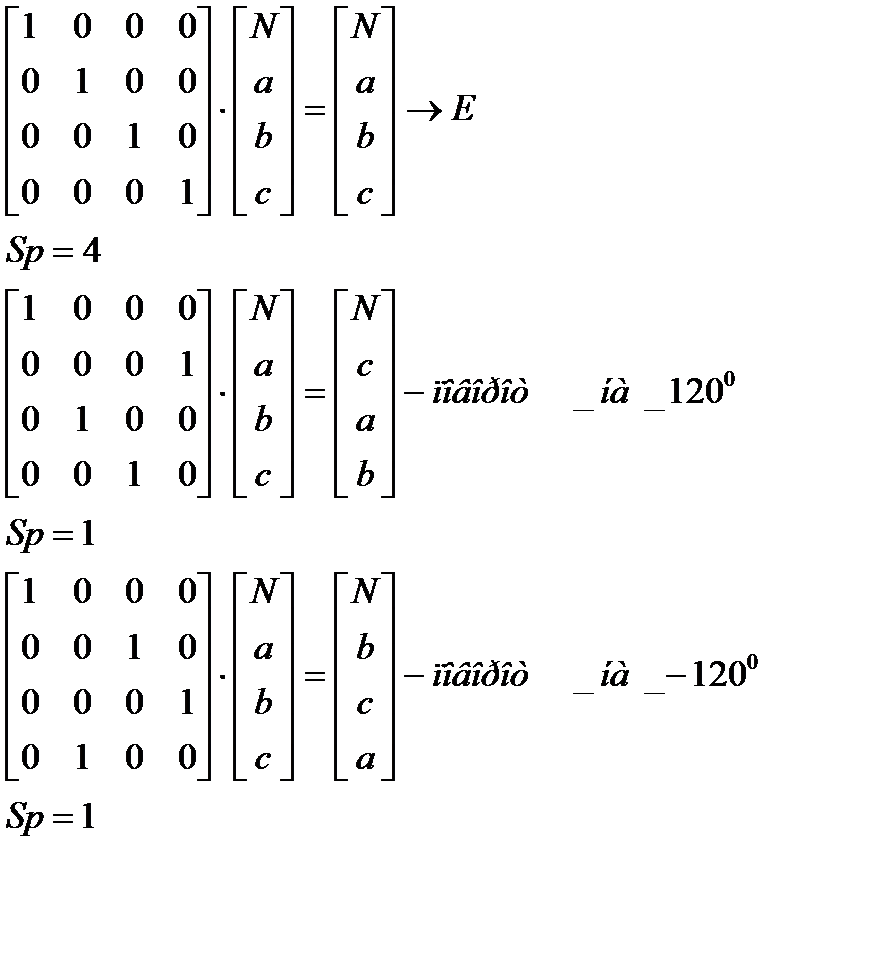
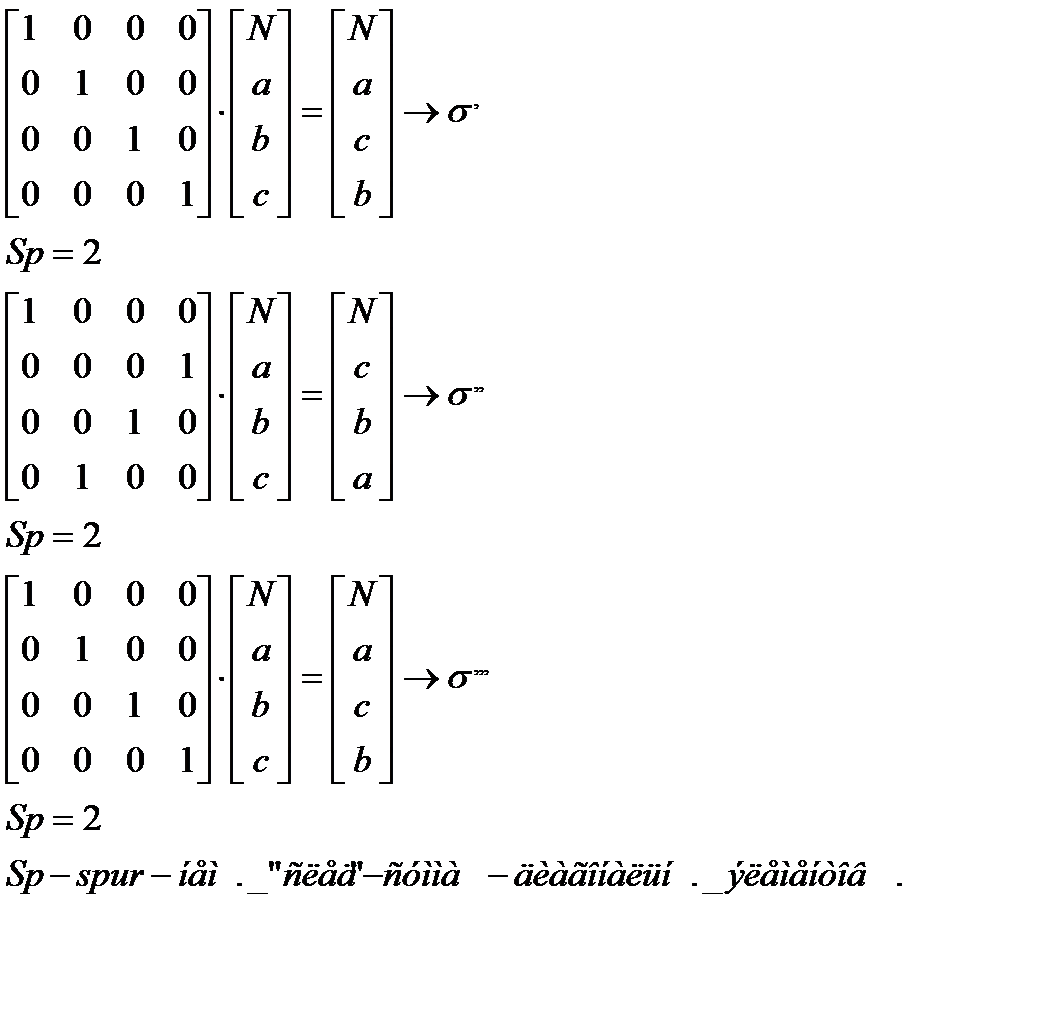
Для того, чтобы преобразование симметрии, выполняемое с любой молекулой характеризовать с помощью конечного числа матриц, необходимо исходные матрицы преобразовать к блочно-диагональному виду. (ненулевые элементы только на диагонали)
Преобразование подобия – математическое преобразование, которое не меняет смысла матрицы, шпура но приводит ее к блочно-диагональному виду.
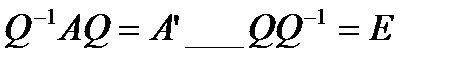
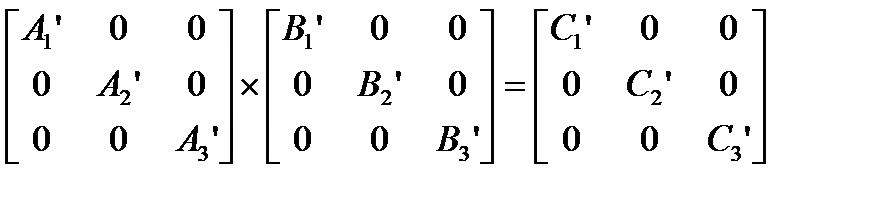
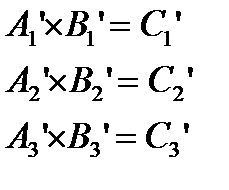
Число подблоков конечно. Полное представление не меняется, шпур также остается прежним.
Непреводимые представления – набор сумм диагональных элементов подматриц, получаемых после исчерпывающего преобразования подобия, выполняемого из исходного состояния матриц операциями симметрии.

Класс операции – операции одного типа с одним и тем же характером представления
Таблица 2 Таблица характеров (выделены НП)
| С3v | E | 2С3 | 3sv |
| А1 | |||
| А2 | -1 | ||
| Е | -1 | ||
| Г |
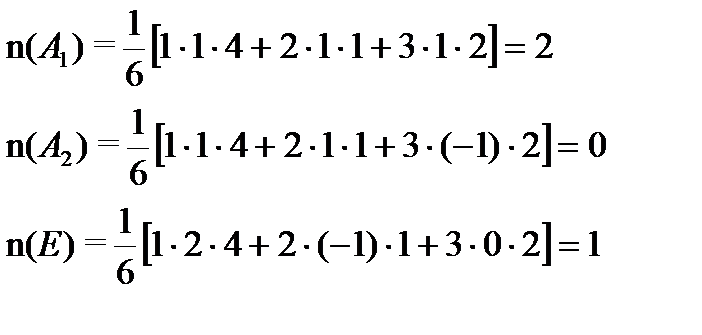
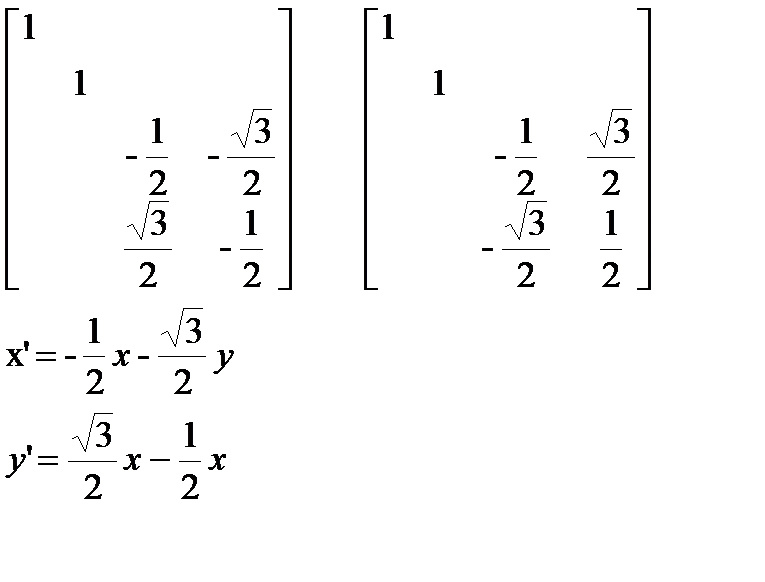

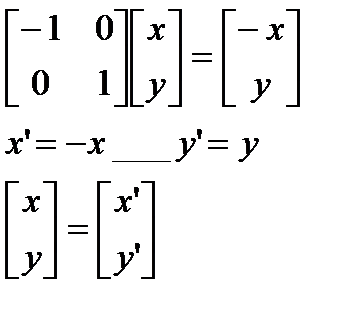
Элементы движения тоже описываются элементами симметрии
Н20: (ось высшего порядка вдоль оси z)
| С2v | E | C2 | sv(yz) | sv(xz) |
| A1 | ||||
| A2 | -1 | -1 | ||
| B1 | -1 | -1 | ||
| B2 | -1 | -1 |
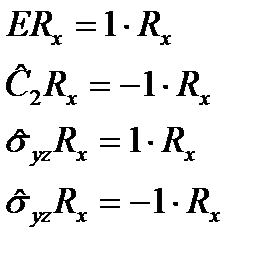

Символы, обозначающие НП
1) Невырожденное НП, симметричное отклонение главной оси, обозначается А
2) Невырожденное НП, антисимметричное относительно главной оси, В
3) 2х вырожденное НП – Е
4) 3х вырожденное НП – Т
(4х вырожденное представление – икосаэдр)
Индексы:
1 – симметрично относительно какого-то другого элемента
2 – антисимметрично
Чтобы отличить одноименные НП по отношению к разным элементам симметрии используются индексы 3, 4, 5…
В точечных группах с горизонтальной плоскостью используются индексы ‘ и ‘’
· ‘ – симметрия относительно горизонтальной плоскости
· ‘’ – антисимметрия
Где есть центр инверсии ставят индексы g и u:
g – симметрия
u – антисимметрия
Бесконечные точечные группы C¥V и D¥h
| C¥V | E | 2C¥ | ¥sV |
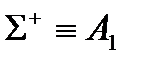
| |||
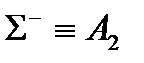
| -1 | ||
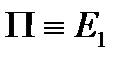
| cosj | ||
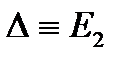
| cosj | ||
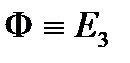
| |||
| ….. | …. | … | .. |
| D¥h | E | 2C¥ | i | 2S¥ | ¥sV |
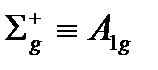
| |||||
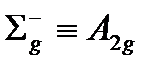
| |||||
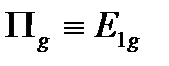
| |||||
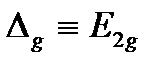
| |||||
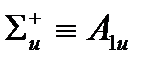
| |||||
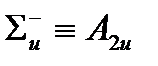
| |||||
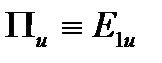
| |||||
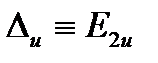
|
Вторая система обозначений связана с l для линейных молекул
Лекция 6
Классификация МО по симметрии
В теории МО многоатомная молекула трактуется так же как и многоэлектронный атом, с той разницей, что молекула создает сложнее поле, зависящее от ядер и их геометрии в пространстве
Геометрию ядер можно отнести к точечной группе симметрии, а поскольку электроны движутся по всей молекуле, то и МО можно характеризовать по симметрии.
| С2v | E | C2 | sv(yz) | sv(xz) |
| A1 | ||||
| A2 | -1 | -1 | ||
| B1 | -1 | -1 | ||
| B2 | -1 | -1 |

Групповые орбитали – линейная комбинация одноименных орбиталей разных атомов, которая выполняется для построения орбиталей, обладающих симметрией. Это промежуточный этап построения МО.
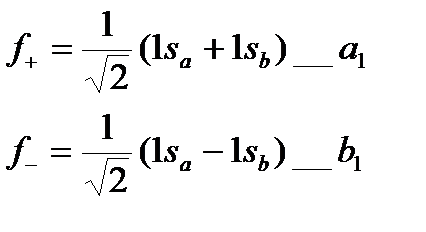
Гибридизация – математический прием, при котором берется линейная комбинация атомных орбиталей одного и того же атома с одинаковой симметрией
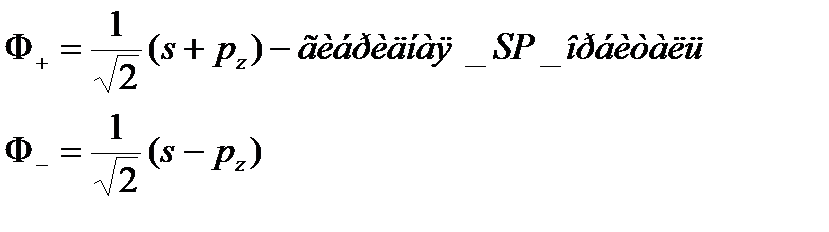

У гибридной орбитали нет собственного значения энергии.
Канонические МО – делокализованы, имеют конкретную энергию, являются решением уравнения Шредингера
Локализованные МО – используются для некоторых целей (для наглядности).
Не обладают симметрией, не имеют конкретной энергии.
Для определения терма
1) Записать электронную конфигурацию
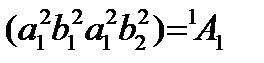
2) Каждое НП возводим в степень количества электронов и меремножаем
Переносим 1 электрон с верхней b2 на a1:
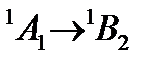
Переносим 1 электрон с верхней b2 на b*1
| * | b1 | -1 | -1 | |||
| b2 | -1 | -1 | 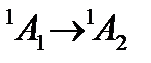
| |||
| A2 | -1 | -1 |

| С3v | E | 2С3 | 3sv | |
| А1 | SN PZ | |||
| А2 | -1 | |||
| Е | -1 | (Px, Py) |
| E | C13 | C23 | s’V | s’’V | s’’’V |
| Sa | Sb | Sc | Sa | Sc | Sb |
| Sb | Sc | Sa | Sc | Sb | Sa |
| Sc | Sa | Sb | Sb | Sa | Sc |
После опраций симметрии берем по очереди характеры и умножаем на результаты проведения опраций симметрии, складываем произведения, отбрасываем коэффициенты, нормируем.
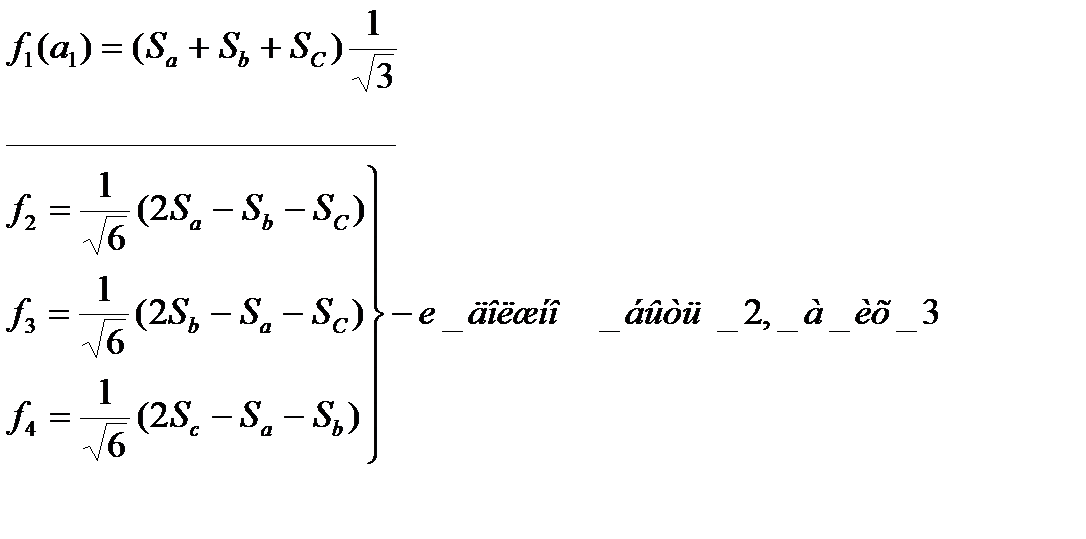
Для построения МО нужен набор независимых функций (ортогональных)
Ортогонализация по Шмидту:
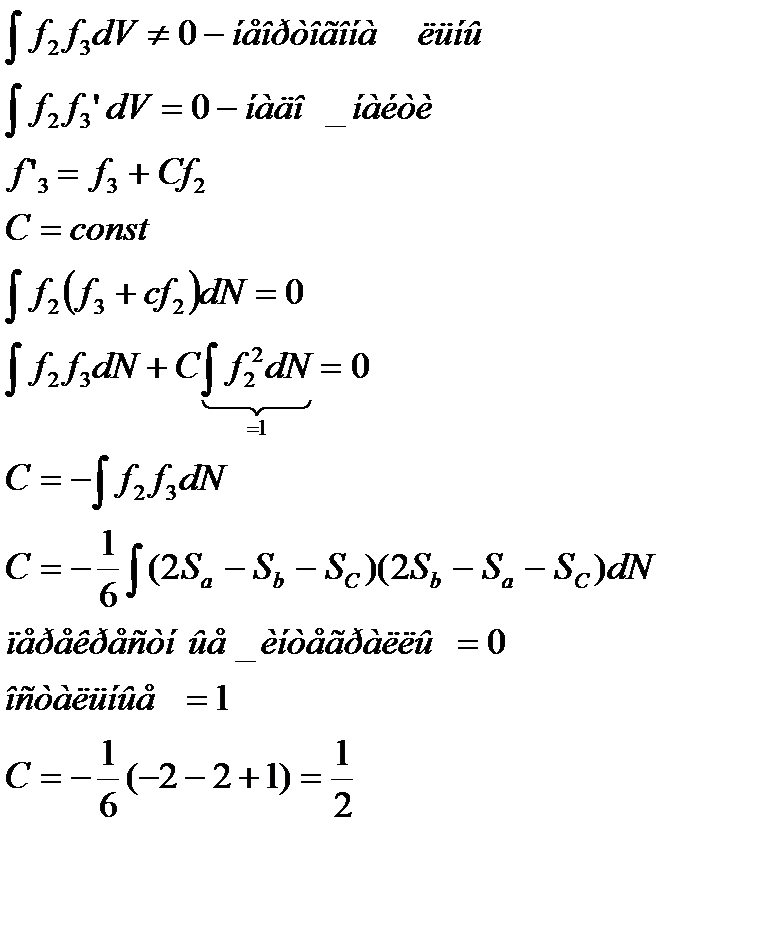


Диаграммы Уолша и геометрия молекул
Диаграммы Уолша показывают изменение относительных орбитальных энергий в зависимости от симметрии молекулы
Молекулы AH2: LiH2+, BeH2,.BH2,:CH2,.NH2, H20
| D¥h | E | 2C¥ | ¥ C2 | i | 2S¥ | ¥sV |
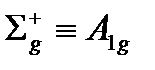
| ||||||
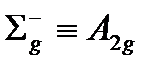
| -1 | -1 | ||||
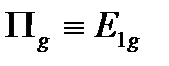
| 2cosj | -2cosj | ||||
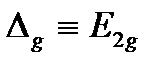
| 2cos2j | 2cos2j | ||||
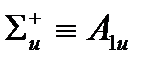
| -1 | -1 | -1 |
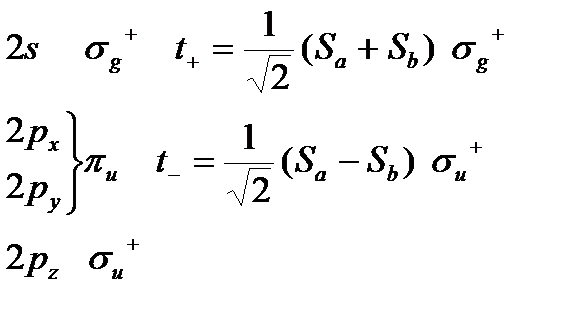





LiH2+ - 2 электрона на нижней a1 – угловая молекула
BeH2 – 4 электрона на 2х нижних s+g и s+u - линейная
BH2 - угловая
:CH2 – синглетный угловой, триплетный тоже угловой
Дальше молекулы всегда угловые
Лекция 7
Основы теории строения координационных соединений
1. Теория кристаллического поля (ТКП) (CFT)
2. Теория поля лигандов (ТПЛ) (LFT)
СFT
· взаимодействие между ионом комплексообразователя и лигандами чисто электростатическое
· лиганды рассматриваются как точечные отрицательные заряды, расположенные определенным образом и создающие поле определенной симметрии
· у иона комплексообразователя взаимодействуют только только d-орбитали,
При взаимодействиях лиганд-комплексообразователь в явном виде участвуют только волновые функции d-орбиталей.
Характерные симметрии комплексов:
· октаэдр Оh
· тетраэдр Td
· плоский квадрат или искаженный октаэдр D4h
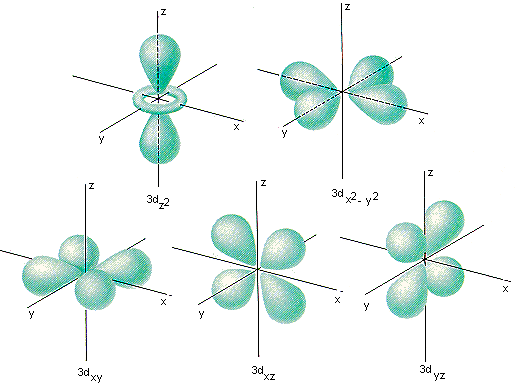
Все d-орбитали четные
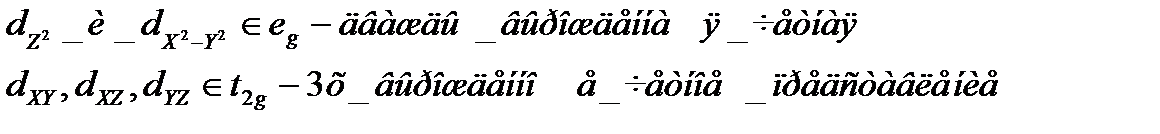

10Dq – энергия расщепления кристаллическим полем d – уровней
Теорема центра тяжести:
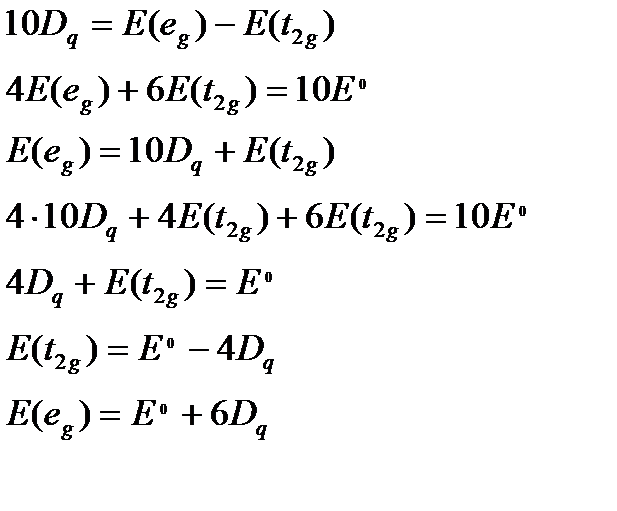
ЭСКП – энергия стабилизации кристаллическим полем (CFSE)

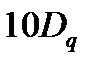 чаще всего определяют из спектров
чаще всего определяют из спектров





Во всех случаях реализуется конфигурация с более низкой энергией
Комплексы с более чем 3-мя электронами делятся на высокоспиновые и низкоспиновые.
Высокоспиновые = комплексы слабого поля
Низкоспиновые = комплексы сильного поля





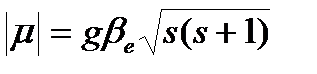 - для чисто спинового магнитного момента
- для чисто спинового магнитного момента
Орбитальный вклад у электронов 1го переходного периода почти отсутствует
Величина 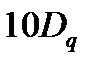 зависит от заряда центрального иона и от природы лиганда. ТКП не может это объяснить. (обнаружено в спектрах поглощения)
зависит от заряда центрального иона и от природы лиганда. ТКП не может это объяснить. (обнаружено в спектрах поглощения)
Оказалось, что лиганды можно расположить в ряд по увеличению 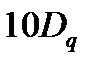

Спектрохимический ряд лигандов:
Date: 2015-05-19; view: 868; Нарушение авторских прав