Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Одноэлектронный водородоподобный атом
|
|
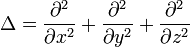— оператор Лапласа (он же Ñ2).
Перейдем к сферическим координатам (переход громоздкий, поэтому лучше заучить конечный вариант)
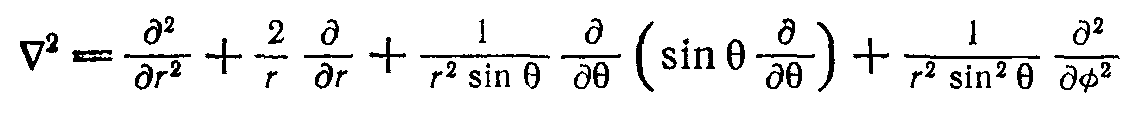
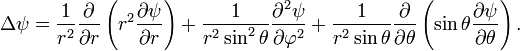
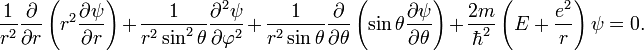
Произведем замену
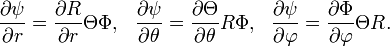
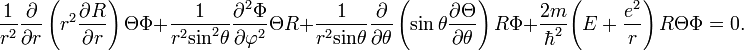
Умножим на r2sin2q
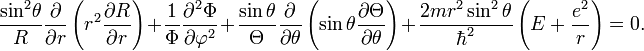
Второе слагаемое тут зависит только от φ. Перенесём его в правую часть равенства.
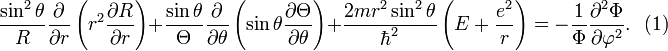
Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим её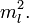 
Следовательно,
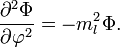
Решением этого уравнения являются функции
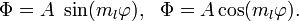
Угол φ может изменяться от 0 до 2π. Функция Φ должна быть периодической с периодом 2π. Это возможно, только если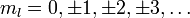 
Таким образом, из решения уравнения Шрёдингера получаем значение одного из квантовых чисел (конечно, из него можно получить их все). Число ml называется магнитным квантовым числом.
Далее, интегрируя квадрат модуля функции Φ от 0 до 2π и приравнивая полученное выражение к единице, получим, что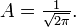 
Далее рассмотрим левую часть уравнения (1). Она, конечно, равна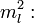 
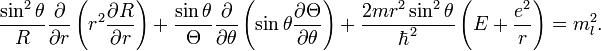
Разделим уравнение на sin 2θ:
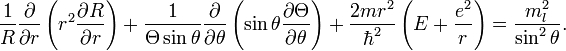
После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через β, получаем
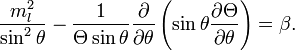
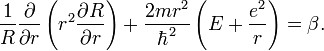
Решение этих двух последних уравнений приводит к значениям l и n соответственно. Три квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода. Число n называется главным квантовым числом. Оно может иметь значения от 1 до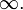 
Число l называется азимутальным квантовым числом и определяет орбитальный момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).
Радиальную часть волновой функции можно записать как (для атома водорода Z=1):
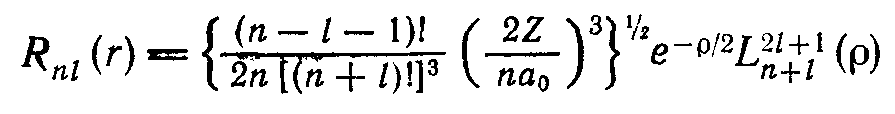
Магнитное квантовое число ml определяет проекцию орбитального момента количества движения на выбранную ось в магнитном поле. Эта проекция равна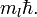 
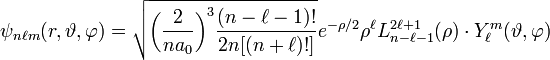
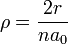
a 0 – боровский радиус,
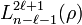обобщенный полином Лагерра степени n − ℓ − 1, (он определяется разными авторами по-разному, например в предыдущей формуле по Фларри он определен для n + ℓ)
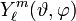- сферическая гармоническая функция степени ℓ порядка m.
Квантовые числа имеют следующие значения:
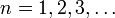
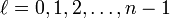
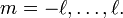
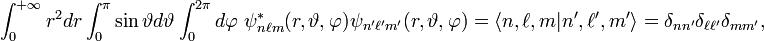Кроме того, эта волновая функция нормированна.
Date: 2015-05-19; view: 597; Нарушение авторских прав