Угловой момент

Собственные значения для оператора углового момента:

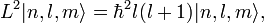
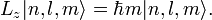
Задача решается в сферических координатах, поскольку атом имеет сферич. Эквипот. Поверхности. нач. коорд. помещ в центр тяж. (ядро)

(помнить 5 постулатов кв. мех.)

1 Состояние сист. опис-ся волн. ф-цией, которая явл. ф-цией координат и врем.

(ВФ обладает след. св-вами: однозначность, непрерывность, дифференцируемость, конечность, квадратичная интегрируемость.)

2 Св-ва сист. описывается динамич. оператором. (оператор должен быть линейным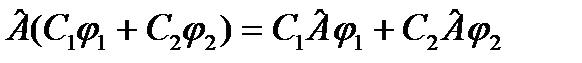

и эрмитовым )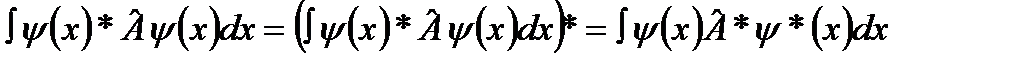

3 Если оператор меняет ф-цию до пост. величины, то говорят о собственной ф-цией данного оператора, а постоянная наз. соб знач.

4 Во всех случаях действует временное уравнение Шредингера.

5 (постулат о среднем)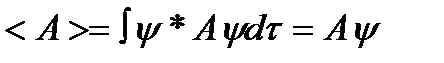

Оператор Гамельтона переводится в сферич. координаты.

Квантовых чисел всегда столько, сколько степеней свободы у системы.

Энергия зависит только от одного кв. числа.

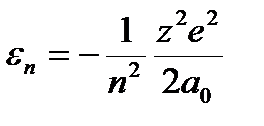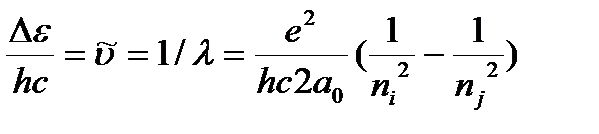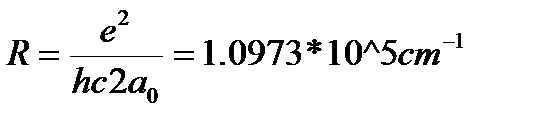, , , -постоянная Ридберга

l: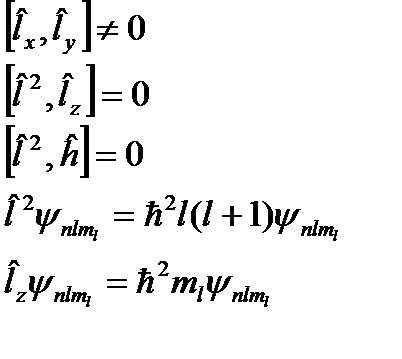

Энергетич. состояния водородопод. ат можно охарактеризовать диаграммой

Date: 2015-05-19; view: 714; Нарушение авторских прав