
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Опыт Штерна и Герлаха. Орбитальный магнитный момент.В квантовой теории магнитный момент μ и механический момент М атома следует заменить операторами и : (13.46)
|
|
Орбитальный магнитный момент. В квантовой теории магнитный момент μ и механический момент М атома следует заменить операторами 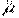 и
и 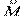 :
:
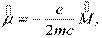 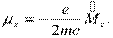
| (13.46) |
Отсюда следует, что изучение свойств магнитного момента электрона сводится к изучению свойств операторов 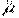 и
и 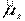 . А так как операторы
. А так как операторы 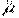 и
и 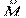 ,
,  и
и 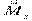 отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам.
отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам.
В стационарном состоянии определенные значения могут иметь только модуль магнитного момента 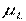 и одна из его проекций на произвольную ось Z. Имея в виду (13.46), а также (13.34) и (13.36), запишем собственные значения операторов
и одна из его проекций на произвольную ось Z. Имея в виду (13.46), а также (13.34) и (13.36), запишем собственные значения операторов 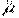 и
и 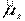 :
:
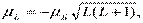 L = 0, 1, 2,... L = 0, 1, 2,...
| (13.47) | |
| μLz = -μБ mL, mL = 0, ± 1, ± 2, …, ± L, | (13.48) | |
где μБ — магнетон Бора: μБ = eћ/2mc. Он играет роль кванта магнитного момента (точнее его проекции μz).
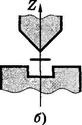
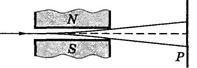
Опыты Штерна и Герлаха. Наличие у атомов магнитных моментов и их квантование было доказано экспериментально Штерном и Герлахом (1921). В их опытах пучок атомов пропускался сквозь сильно неоднородное поперечное магнитное поле (рис. 13.10, а). Необходимая степень неоднородности поля достигалась с помощью специальной формы полюсных наконечников N и S электромагнита (рис. 13.10, б). После прохождения магнитного поля пучок атомов попадал на фотопластинку Р и оставлял на ней след.

а)
Рис. 13.10.
Если атомы обладают магнитным моментом, то согласно электродинамике на них будет действовать сила, проекция которой на ось Z (см. рис. 13.10, б)
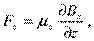
| (13.49) |
где μ z — проекция магнитного момента атома на ось Z. Из этой формулы видно, что для получения необходимого эффекта при малых значениях μ z нужно обеспечить достаточно большую неоднородность поля, т. е. ∂Bz/∂z. Это и достигалось с помощью указанной формы полюсных наконечников.
В отсутствие магнитного поля след пучка на фотопластинке ^ Р имел вид одной полоски (z = 0). При включении же магнитного поля наблюдалось расщепление пучка (рис. 13.10, в), что являлось следствием квантования проекции магнитного момента μ z в формуле (13.49): μ z может принимать только ряд дискретных значений. В опытах обнаружилось также, что для разных атомов число компонент, на которые расщеплялся пучок, было или нечетным, или четным. Анализ полученных результатов показал, что нечетное число компонент возникает у атомов, обладающих только орбитальным механическим моментом ML, тогда магнитное поле снимает вырождение по L и число компонент (значений mL) будет равно 2 L + 1, т. е. нечетным.
Если же момент атома является суммой орбитального и спинового, т. е. определяется квантовым числом ^ J, то число компонент будет равно 2 J + 1, и в зависимости от того, полуцелым или целым будет значение J, число компонент будет соответственно четным или нечетным.
^ Спиновый магнитный момент. Зная степень неоднородности магнитного поля, т. е. дВг/дг, Штерн и Герлах по величине расщепления пучка на фотопластинке рассчитали значение проекции спинового магнитного момента на направление магнитного поля, μB. Выяснилось, что μB равен одному магнетону Бора. Этот результат приводит к гиромагнитному отношению вдвое превышающему гиромагнитное отношене для орбитальных моментов. В связи с этим говорят, что спин обладает удвоенным магнетизмом.
Итак, спиновый магнитный момент и его проекция на произвольную ось Z определяются как
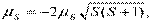
| (13.50) |
| μSz = -2 μБ ms, ms=S,S- 1, …, -S. | (13.51) |
При S = 1/2 ms = +1/2 и -1/2.
Принято говорить, что спиновый магнитный момент электрона равен одному магнетону Бора. Такая терминология обусловлена тем, что при измерении магнитного момента мы обычно измеряем его проекцию, а она как раз и равна одному μ Б. Опыты Штерна и Герлаха явились еще одним убедительным доказательством наличия у электрона спина. Помимо этих опытов следует упомянуть и о так называемых магнитомеханических явлениях — опытах Эйнштейна и де Хааса, а также опыте Барнетта. И в этих опытах было обнаружено, что гиромагнитное отношение спиновых моментов тоже вдвое больше отношения орбитальных.
^ Полный магнитный момент атома. Вследствие удвоенного магнетизма спина гиромагнитное отношение полных моментов μ/MJ оказывается значительно более сложным. Оно зависит от квантовых чисел L, S и J. Соответствующий расчет, проводимый в квантовой теории, позволил найти магнитный момент μ и его проекцию на ось Z:
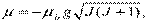
| (13.52) |
| μ z = - μ Б gmJ, mJ = J, J -1, …, - J, | (13.53) |
где g — множитель (или фактор) Ланде
В частности, в синглетных состояниях (S = 0) J = L, g = 1, и мы приходим к формулам (13.47) и (13.48). А при L = 0 (J = S, g = 2) — к формулам (13.50) и (13.51).
Date: 2015-05-18; view: 693; Нарушение авторских прав