Соотношение неопределенностей Гейзенберга. В 1927 г. немецкий физик-теоретик В

В 1927 г. немецкий физик-теоретик В. Гейзенберг сформулировал принцип неопределенности, заключающийся в принципиальной невозможности одновременно точно определить положение микрочастицы в пространстве и ее импульс:

Δ p_x · Δ x ≥ h / 2π,

где Δ p_x = m Δ v_x x - неопределенность (ошибка в определении) импульса микрообъекта по координате х; Δ x - неопределенность (ошибка в определении) положения микрообъекта по этой координате.
Таким образом, чем точнее определена скорость, тем меньше известно о местоположении частицы, и наоборот.
Поэтому для микрочастицы становится неприемлемым понятие о траектории движения, поскольку оно связано с конкретными координатами и импульсом частицы. Можно лишь говорить о вероятности обнаружить ее какой-то областях пространства.
Произошел переход от "орбит движения" электронов, введенных Бором, к понятию орбитали - области пространства, где вероятность пребывания электронов максимальна.

Потенциальный барьер – область пространства, где потенциальная энергия частицы (или тела) выше, чем в соседних областях. Рассмотрим простейший потенциальный барьер прямоугольной формы шириной а и высотой U₀. Вне барьера потенциальная энергия частицы равна нулю. Полная энергия частицы Е равна сумме её кинетической энергии Т и потенциальной U. Вне барьера Е = Т. Если частица двигается на барьер слева и имеет Е = Т < U₀, то с точки зрения классической физики она не может преодолеть его и отразится от него. Действительно, классическая физика требует безусловного сохранения энергии. Если представить, что частица с Е < U₀, вошла внутрь барьера, то она неизбежно должна иметь там отрицательную кинетическую энергию (чтобы её полная энергия сохранилась), что невозможно по смыслу кинетической энергии.
С точки зрения квантовой физики частица с Е < U₀ может с некоторой вероятностью пройти сквозь барьер. Это явление носит название туннельного эффекта.
Вероятность прохождения частицы массы m через барьер D определяется соотношением

где .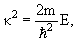
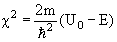Основная зависимость коэффициента прохождения D от ширины a и высоты барьера U₀ определяется экспоненциальным множителем e^-χa.

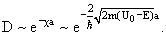
В случае a ~ 10^{-13 см, m ~ 10-24 г для (U}₀ − E) ~ 10 МэВ D ~ 1/e.
То есть частица (протон, α-частица) с заметной вероятностью может пройти сквозь потенциальный барьер, превышающий её энергию на 5–10 МэВ.

Квантовые числа – целые или дробные числа, определяющие возможные значения физических величин, характеризующих квантовую систему (молекулу, атом, атомное ядро, элементарную частицу). Квантовые числа отражают дискретность (квантованность) физических величин, характеризующих микросистему. Набор квантовых чисел, исчерпывающе описывающих микросистему, называют полным. Так состояние электрона в атоме водорода определяется четырьмя квантовыми числами: главным квантовым числом n (может принимать значения 1, 2, 3, …), определяющим энергию Е_n электрона (Е_n = -13.6/n² эВ); орбитальным квантовым числом l = 0, 1, 2, …, n – 1, определяющим величину L орбитального момента количества движения электрона (L = ћ[ l (l + 1)]^1/2); магнитным квантовым числом m < ± l, определяющим направление вектора орбитального момента; и квантовым числом m_s = ± 1/2, определяющим направление вектора спина электрона.

Date: 2015-05-18; view: 495; Нарушение авторских прав