
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные квантовые числа
|
|
| n | Главное квантовое число: n = 1, 2, … 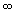 . .
|
| j | Квантовое число полного углового момента. j никогда не бывает отрицательным и может быть целым (включая ноль) или полуцелым в зависимости от свойств рассматриваемой системы. Величина полного углового момента J связана с j соотношением J2 = ћ2j(j + 1).  = = 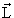 + + 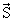 , где , где 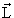 и и 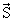 векторы орбитального и спинового угловых моментов. векторы орбитального и спинового угловых моментов.
|
| l | Квантовое число орбитального углового момента l может принимать только целые значения: l = 0, 1, 2, … ∞. Величина орбитального углового L момента связана с l соотношением L2 = ћ2 l (l + 1). |
| m | Магнитное квантовое число. Проекция полного, орбитального или спинового углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента mj = j, j-1, j-2, …, - (j-1), - j. Для орбитального момента m l = l, l -1, l -2, …, -(l -1), - l. Для спинового момента электрона, протона, нейтрона, кварка m s = ±1/2 |
| s | Квантовое число спинового углового момента s может быть либо целым, либо полуцелым. s - неизменная характеристика частицы, определяемая ее свойствами. Величина спинового момента S связана с s соотношением S2 = ћ2s(s + 1). |
| P | Пространственная четность. Она равна либо +1, либо -1 и характеризует поведение системы при зеркальном отражении. P = (-1) l. |
Существование сохраняющихся (неизменных во времени) физических величин для данной системы тесно связано со свойствами симметрии этой системы. Так, если изолированная система не изменяется при произвольных поворотах, то у неё сохраняется орбитальный момент количества движения. Это имеет место для атома водорода, в котором электрон движется в сферически симметричном кулоновском потенциале ядра и поэтому характеризуется неизменным квантовым числом l. Внешнее возмущение может нарушать симметрию системы, что приводит к изменению самих квантовых чисел. Фотон, поглощенный атомом водорода, может “перебросить” электрон на другую орбиту с другими значениями квантовых чисел.
Помимо квантовых чисел, отражающих пространственно-временную симметрию микросистемы, существенную роль у частиц играют так называемые внутренние квантовые числа. Ряд из них, такие как спин и электрический заряд, сохраняются во всех взаимодействиях, другие в некоторых взаимодействиях не сохраняются. Так кварковое квантовое число странность, сохраняющееся в сильном взаимодействии, не сохраняется в слабом взаимодействии, что отражает разную природу этих взаимодействий. Внутренним квантовым числом для кварков и глюонов является также цвет. Цвет кварков может принимать три значения, цвет глюонов – восемь.
Date: 2015-05-18; view: 671; Нарушение авторских прав