Туннельный эффект. Туннельный эффект (туннелирование) - квантовый переход системы через область движения, запрещённую классич

ТУННЕЛЬНЫЙ ЭФФЕКТ (туннелирование) - квантовый переход системы через область движения, запрещённую классич. механикой. Типичный пример такого процесса- прохождение частицы через потенциальный барьер, когда её энергия 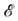меньше высоты барьера. Импульс частицы р в этом случае, определяемый из соотношения 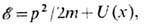где U(x) - потенц. энергия частицы (т - масса), был бы в области внутри барьера, мнимой величиной. В квантовой механике благодаря неопределённостей соотношению между импульсом и координатой подбарьерное движение оказывается возможным. Волновая ф-ция частицы в этой области экспоненциально затухает, и в квазиклассич. случае (см. Квазиклассическое приближение)её амплитуда в точке выхода из-под барьера мала.

Одна из постановок задач о прохождении потенц. барьера соответствует случаю, когда на барьер падает стационарный поток частиц и требуется найти величину прошедшего потока. Для таких задач вводится коэф. прозрачности барьера (коэф. туннельного перехода) D, равный отношению интенсивностей прошедшего и падающего потоков. Из обратимости по времени следует, что коэф. прозрачности для переходов в "прямом" и обратном направлениях одинаковы. В одномерном случае коэф. прозрачности может быть записан в виде

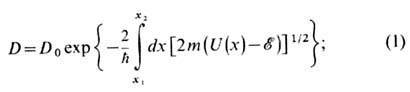
интегрирование проводится по классически недоступной области, х _1,2 - точки поворота, определяемые из условия 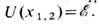В точках поворота в пределе классич. механики импульс частицы обращается в нуль. Коэф. D ₀ требует для своего определения точного решения кван-тово-механич. задачи.

При выполнении условия квазиклассичности

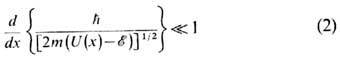
на всём протяжении барьера, за исключением непосредств. окрестностей точек поворота x _1,2 коэф. D ₀ слабо отличается от единицы. Существ. отличие D ₀ от единицы может быть, напр., в тех случаях, когда кривая потенц. энергии с одной из сторон барьера идёт настолько круто, что квазиклассич. приближение там неприменимо, или когда энергия близка к высоте барьера (т. е. выражение, стоящее в экспоненте, мало). Для прямоугольного барьера высотой U _о и шириной а коэф. прозрачности определяется ф-лой
где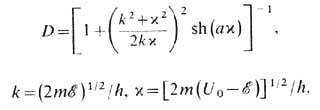

Основание барьера соответствует нулевой энергии. В квазиклассич. случае D мал по сравнению с единицей.

Др. постановка задачи о прохождении частицы через барьер состоит в следующем. Пусть частица в нач. момент времени находится в состоянии, близком к т. н. стационарному состоянию, к-рое получилось бы при непроницаемом барьере (напр., при барьере, приподнятом вдали от потенциальной ямы на высоту, большую энергии вылетающей частицы). Такое состояние наз. квазистационарным. Аналогично стационарным состояниям зависимость волновой ф-ции частицы от времени даётся в этом случае множителем 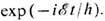В качестве энергии здесь фигурирует комплексная величина Е, мнимая часть к-рой определяет вероятность распада квазистационарного состояния в единицу времени за счёт Т. э.:

В квазиклассич. приближении вероятность, даваемая ф-лой (3), содержит экспоненц. множитель того же типа, что и в-ф-ле (1). В случае сферически симметричного потенц. барьера вероятность распада квазистационарного состояния с орбит. квантовым числом l определяется ф-лой

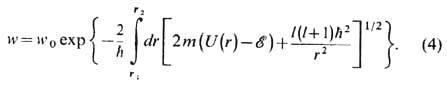
Здесь r _1,2-радиальные точки поворота, подынтегральное выражение в к-рых равно нулю. Множитель w₀ зависит от характера движения в классически разрешённой части потенциала, напр. он пропорц. классич. частоте колебаний частицы между стенками барьера.

Т. э. позволяет понять механизм a-распада тяжёлых ядер. Между -частицей и дочерним ядром действует элек-тростатич. отталкивание, определяемое ф-лой На малых расстояниях порядка размера а ядра ядерные силы таковы, что эфф. потенциал можно считать отрицательным: 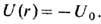В результате вероятность а -распада даётся соотношением

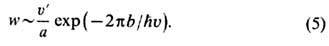
Здесь -энергия вылетающей a-частицы.

Т. э. обусловливает возможность протекания термоядерных реакций на Солнце и звёздах при темп-ре в десятки и сотни млн. градусов (см. Эволюция звёзд),а также в земных условиях в виде термоядерных взрывов или УТС.

В симметричном потенциале, состоящем из двух одинаковых ям, разделённых слабопроницаемым барьером, Т. э. приводит к интерференциисостояний в ямах, что приводит к слабому двойному расщеплению дискретных уровней энергии (т. н. инверсионное расщепление; см. Молекулярные спектры). Для бесконечного периодичного в пространстве набора ям каждый уровень превращается в зону энергий. Таков механизм образования узких электронных энергетич. зон в кристаллах с сильной связью электронов с узлами решётки.

Если к полупроводниковому кристаллу приложено элек-трич. поле, то зоны разрешённых энергий электронов становятся наклонными в пространстве. Тем самым уровень пост. энергии электрона пересекает все зоны. В этих условиях становится возможным переход электрона из одной энергетич. зоны в другую за счёт Т. э. Классически недоступной областью при этом является зона запрещённых энергий. Это явление наз. пробоем Зинера. Квазиклассич. приближение отвечает здесь малой величине напряжённости электрич. поля. В этом пределе вероятность пробоя Зинера определяется в осн. экспонентой, в показателе к-рой стоит большая отрицат. величина, пропорциональная отношению ширины запрещённой энергетич. зоны к энергии, набираемой электроном в приложенном поле на расстоянии, равном размеру элементарной ячейки.

Похожий эффект проявляется в туннельных диодах, в к-рых зоны наклонены благодаря полупроводникам р - и n -типа по обе стороны от границы их соприкосновения. Туннелирование осуществляется благодаря тому, что в зоне, куда переходит носитель заряда, имеется конечная плотность незанятых состояний.

Благодаря Т. э. возможен электрич. ток между двумя металлами, разделёнными тонкой диэлектрич. перегородкой. Эти металлы могут находиться как в нормальном, так и в сверхпроводящем состоянии. В последнем случае может иметь место Джозефсона эффект.

Т. э. обязаны такие явления, происходящие в сильных электрич. полях, как автоионизация атомов (см. Ионизация полем)и автоэлектронная эмиссия из металлов. В обоих случаях электрич. поле образует барьер конечной прозрачности. Чем сильнее электрич. поле, тем прозрачнее барьер и тем сильнее электронный ток из металла. На этом принципе основан сканирующий туннельный микроскоп - прибор, измеряющий туннельный ток из разных точек исследуемой поверхности и дающий информацию о характере её неоднородности.

Т. э. возможен не только в квантовых системах, состоящих из одной частицы. Так, напр., низкотемпературное движение дислокаций в кристаллах может быть связано с туннелированием конечной части дислокации, состоящей из многих частиц. В такого рода задачах линейную дислокацию можно представить как упругую струну, лежащую первоначально вдоль оси у в одном из локальных минимумов потенциала V(x, у). Этот потенциал не зависит от у, а его рельеф вдоль оси х представляет собой последовательность локальных минимумов, каждый из к-рых находится ниже другого на величину, зависящую от приложенного к кристаллу механич. напряжения. Движение дислокации под действием этого напряжения сводится к туннелированию в соседний минимум определ. отрезка дислокации с последующим подтягиванием туда оставшейся её части. Такого же рода туннельный механизм может отвечать за движение волн зарядовой плотности в диэлектрике Пайерлса (см. Пайерлса переход).

Для расчётов эффектов туннелирования таких многоразмерных квантовых систем удобно использовать квазиклассич. представление волновой ф-ции в виде 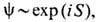где S -классич. действие системы. Для Т. э. существенна мнимая часть S, определяющая затухание волновой ф-ции в классически недоступной области. Для её вычисления используется метод комплексных траекторий.

Квантовая частица, преодолевающая потенц. барьер, может быть связана с термостатом. В классич. механике это соответствует движению с трением. Тем самым, для описания туннелирования необходимо привлечение теории, получившей назв. диссипативной квантовой механики. Такого рода соображения необходимо использовать для объяснения конечного времени жизни токовых состояний контактов Джозефсона. В этом случае происходит туннелирование эфф. квантовой частицы через барьер, а роль термостата играют нормальные электроны.

Лит.: Ландау Л. Д., Лифшиц Е. М., Квантовая механика, 4 изд., М., 1989; Займан Дж., Принципы теории твердого тела, пер. с а

Date: 2015-05-18; view: 794; Нарушение авторских прав