
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Реологические свойства жидких сред
|
|
К реологическим свойствам жидких сред, определяющим их текучесть, относятся вязкость и предельное напряжение сдвига.
Вязкость – свойство жидкостей оказывать сопротивление их сдвиговому течению. Силы, возникающие при скольжении слоев жидкости относительно друг друга, называются внутренними силами трения, а жидкости, в которых это трение возникает, называются вязкими.
В соответствии с законом Ньютона сила внутреннего трения пропорциональна скорости сдвига жидкости и площади соприкасающихся сдвигаемых слоев:
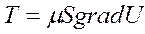 ,
,
где Т – сила внутреннего трения; S –площадь соприкасающихся слоев; m - коэффициент динамической вязкости жидкости; 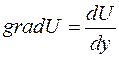 - градиент скорости сдвига; U – скорость сдвига.
- градиент скорости сдвига; U – скорость сдвига.
В результате внутреннего трения в вязкой жидкости возникают касательные напряжения:
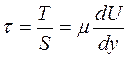 .
.
Следовательно, касательное напряжение в жидкости пропорционально скорости деформации сдвига.
Вязкость можно рассматривать как меру передачи движения частиц жидкости в направлении перпендикулярном скорости их движения.
Эта мера для газов объясняется молекулярным движением, проявлением которого является перенос количества макроскопического движения.
Для коэффициента динамической вязкости газов на основе молекулярно-кинетической теории установлена следующая формула:
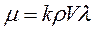 ,
,
где k – постоянная; r - плотность; l - длина свободного пробега молекул; V - среднее значение скорости движения молекул.
В теории вязкости жидкостей принимается, что передача количества движения происходит за счет временного объединения молекул на границе слоев, причем, она будет лишь тогда, когда энергии движения будет достаточно для преодоления силы притяжения между молекулами, и когда они будут определенным образом друг относительно друга.
Коэффициент динамической вязкости жидкости зависит от температуры давления и энергии связи молекул и определяется экспериментальной формулой А.И.Бачинского:
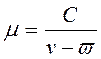 ,
,
где v – удельный объем; C,w - постоянные.
В табл.1.3 приведены значения коэффициентов динамической вязкости некоторых жидкостей.
Таблица 1.3
Коэффициенты динамической вязкости некоторых жидкостей
| Жидкость | t, оС | µ, Па.с |
| Воздух | 0,00002 | |
| Вода | 0,00101 | |
| Керосин | 0,0025 | |
| Нефть легкая | 0,025 | |
| Нефть тяжелая | 0,14 | |
| Смазочное масло | 0,172 | |
| Глицерин | 0,87 |
Кинематическим коэффициентом вязкости называют отношение коэффициента динамической вязкости к плотности жидкости:
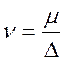 .
.
Реологические свойства гетерогенных (неоднородных) систем (суспензии, коллоидные растворы, эмульсии), в частности дисперсных, закону Ньютона не подчиняются. Из-за сцепления элементарных объемов они имеют напряжения сдвига даже при отсутствии движения.
Такие среды называются структурированными и касательные напряжение в них описываются законом Шведова-Бингама:
 ,
,
где 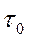 - предельное напряжение сдвига, необходимое для начала течения среды;
- предельное напряжение сдвига, необходимое для начала течения среды; 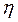 - коэффициент структурной вязкости, Па·с.
- коэффициент структурной вязкости, Па·с.
Структурообразование является результатом энергетического взаимодействия между частицами дисперсной фазы и дисперсионной средой.
Для бесструктурных суспензий 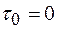 , а коэффициент структурной вязкости становится равным коэффициенту динамической вязкости.
, а коэффициент структурной вязкости становится равным коэффициенту динамической вязкости.
Из законов Ньютона и Шведова-Бингама следует:
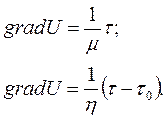
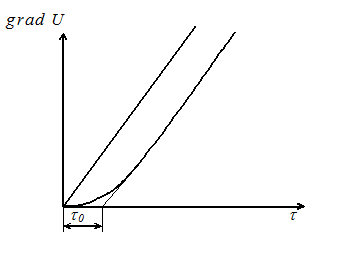
Рис.1.1. Графическая интерпретация законов Ньютона и Шведова-Бингама.
Date: 2015-05-18; view: 1347; Нарушение авторских прав