Стационарные состояния в квантовой механике

Состояние квантовой системы, в котором ее энергия имеет определенное значение, а среднее значение всех других физических величин, характеризующих систему, не меняются с течением времени, называется стационарным.

Выявим условия стационарности состояния квантовой системы. Воспользуемся для этого шредингеровским представлением описания движения с помощью оператора матрицы плотности .

Из уравнения фон Неймана (15.3)

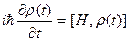
следует, что если коммутатор 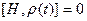, то 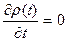. Это означает:

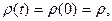(16.1)

т.е. матричные элементы оператора матрицы плотности 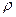не зависят от времени

(16.2)

Физический смысл соотношения (16.2) свидетельствует о том, что вероятности измерения любых величин в этом состоянии системы не зависят от времени (т.к. диагональные матричные элементы матрицы 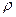имеют смысл вероятности или плотности вероятности). Следовательно, и средние значения этих физических величин не изменяются с течением времени.

Для решения вопроса об энергии системы в этом состоянии рассмотрим случай чистого состояния, когда оно может быть описано в шредингеровском представлении вектором состояния .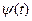

Из формулы матричного оператора 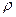в виде

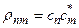(16.3)

и соотношения (16.2) следует вывод о том, что зависимость 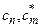от времени может быть лишь типа:

(16.4)

где α - некоторая постоянная. Тогда и волновой вектор будет зависеть от времени таким же образом:

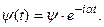(16.5)

Учтем, что вектор состояния является решением волнового уравнения Шредингера

(16.6)

и что левая часть этого уравнения равна

(16.7)

Тогда из соотношений (16.6) и (16.7) следует новое уравнение

(16.8)

Принимая во внимание уравнение для собственных векторов и собственных значений оператора энергии 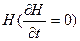для случая дискретного спектра

(16.9)

и сокращая в уравнениях (16.9) и (16.8) временной множитель 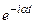, получим

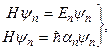(16.10)

откуда следует, что , т.е. энергия в этом состоянии имеет определенное значение 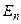. Значит, состояние системы действительно является стационарным.

Уравнение (16.9) получило название стационарного уравнения Шредингера.

Date: 2015-05-18; view: 843; Нарушение авторских прав