Описание электромагнитных волн

Световые волны в вакууме.

Описание электромагнитных волн.

Уравнения Максвелла для ЭМВ, распространяющихся в вакууме при отсутствии токов (j = 0) и зарядов (r = 0) имеют вид: rotH=∂D/dt; rotE=-∂B/dt; divB=0; divD=0; D=ε₀E; B= μ₀H, (1-6), где E и H – напряженности, D и B – индукции электрического и магнитного полей соответственно, e₀ и m₀ – соответственно электрическая и магнитная постоянные. Последние уравнения называются материальными. Именно они учитывают влияние свойств среды на процесс распространения ЭМВ в ней.

Пользуясь уравнениями Максвелла, можно получить волновое уравнение и определить далее основные свойства ЭМВ.

Волновое уравнение для B:

∇²B-(1/c²)(∂²B/∂t²)=0, где введено обозначение: 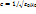— скорость света в вакууме.

Волновое уравнение для поля E:

∇²E-(1/c²)(∂²E/∂t²)=0

Найдем решение этого уравнения для скалярной функции Ф=Ф (r, t). Пусть эта функция является, по крайней мере, дважды дифференцируемой функцией. Исследуем сначала очень важный частный случай – одномерную задачу, когда скалярная функция Ф зависит только от одной из декартовых координат Ф = Ф (z, t). Это означает, что в данный момент времени t при z = const функция Ф имеет вполне определенное значение, одинаковое на всей плоскости z = const. Такое соответствующее поле называется однородным. В этом случае волновое уравнение принимает вид:

∂²Ф/∂z²-(1/c²)(∂²Ф/∂t²)

Используя новые формальные независимые переменные x = z – ct, h = z + ct, получаем

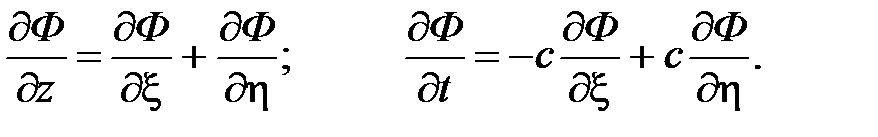
Решая эти дифференциальные уравнения, получаем общее решение в виде:

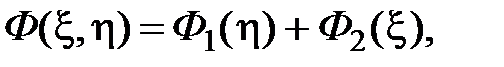
или окончательно в исходных переменных:

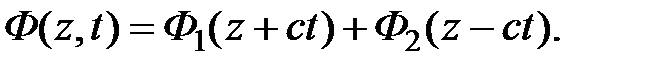
Выясним физический смысл полученного решения волнового уравнения. Сначала проанализируем решение

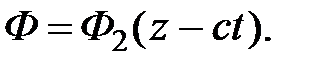
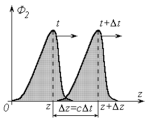График функции Ф ₂ (z) в моменты времени t и t+Dt изображен на рис.. Значение аргумента функции в точке z в момент времени t совпадает со значением аргумента функции в точке z+Dz в момент t+Dt, если Dz=cDt, т.к. z – ct = z + D z – c(t + D t)( D z = c D t). Поэтому функция Ф ₂ (z–ct) описывает волну произвольной формы, движущуюся со скоростью v=Dz/Dt=c в направлении положительных значений оси Z. В процессе движения значение Ф ₂ в каждой точке волны и форма волны не изменяются.

Аналогично функция Ф ₁ (z+ct) описывает волну произвольной формы, движущуюся со скоростью с в направлении отрицательных значений оси Z. Значение Ф₁ в каждой точке волны и форма волны в процессе движения не изменяются.

Значение функции Ф для фиксированных z и t является постоянным на плоскости, перпендикулярной оси Z. Поэтому такие волны называются плоскими.

Сферические волны. Рассмотрим изотропную волну от точечного источника. Тогда решение волнового уравнения будем искать в виде Ф(r,t), где r – расстояние от точечного источника. В сферической системе координат (r, q, j) искомое решение из соображений симметрии не зависит от угловых координат. Тогда волновое уравнение примет вид:

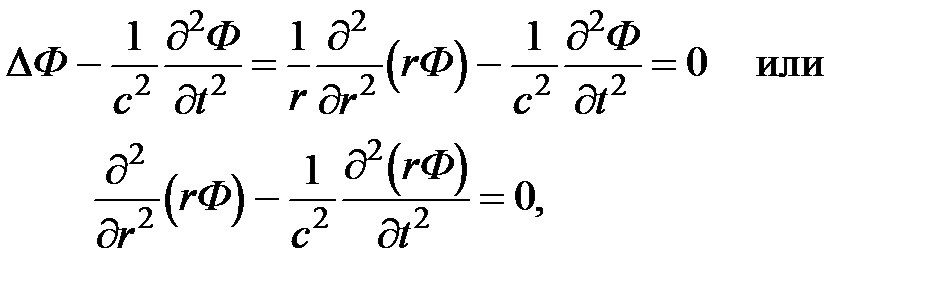Тогда общее решение уравнения имеет вид:

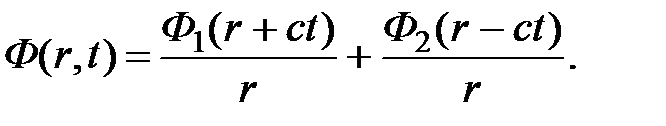
Выясним физический смысл полученного решения. Второе слагаемое представляет собой волну, движущуюся в направлении увеличения значений r, т.е. от центра (точечного источника). Такая волна называется расходящейся. Первое слагаемое описывает волну, движущуюся в направлении уменьшения r, т.е. к центру. Такая волна называется сходящейся. Общее решение является суперпозицией сходящейся и расходящейся волн. Значение Ф в фиксированный момент времени на сфере постоянного радиуса является постоянным. Такие волны называются сферическими.

Плоские гармонические волны. Если Ф ₁ и Ф ₂ являются гармоническими функциями своего аргумента, то волна называется гармонической. Волна, описываемая функцией 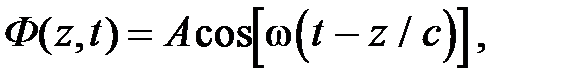называется плоской гармонической волной. Постоянная А называется амплитудой волны, w – ее частотой. Необходимо отметить, что это выражение описывает лишь частный случай плоской гармонической волны, распространяющейся в направлении положительных значений оси Z. Движущуюся волну часто называют бегущей. Общее выражение для бегущей волны в положительном направлении оси Z имеет вид:

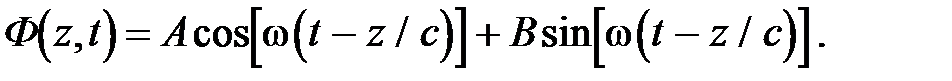Аналогично общее выражение для бегущей волны в отрицательном направлении оси Z имеет вид: 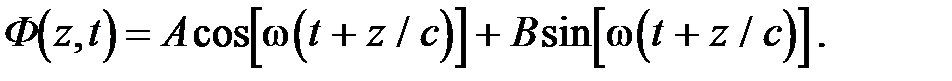Аргумент гармонической функции в этих выражениях называется фазой волны. Тогда, исходя из этого понятия, можно дать другое определение плоской волны. Волна, у которой поверхностями постоянных фаз являются плоскости, называется плоской. Учитывая, что

l = сТ = 2p с/ w: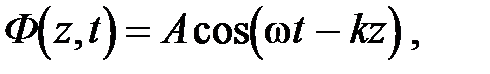

где k = w / c = 2p / l – волновое число.

Волновой вектор. Рассмотрим случай бегущей в положительном направлении оси Z плоской гармонической волны. Введем вектор k, называемый волновым, модуль которого равен волновому числу, а направление совпадает с осью Z. Тогда для произвольной точки с радиус-вектором r: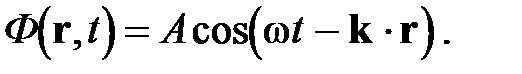

Эта формула не зависит от системы координат и характеризует в общем случае плоскую волну, распространяющуюся в направлении вектора k.

Если для гармонической волны поверхности постоянной фазы такой волны, вообще говоря, не совпадают с поверхностями постоянной амплитуды. В таком случае говорят, что волна неоднородна.

Представление плоской волны в комплексной форме. Принимая во внимание формулу Эйлера

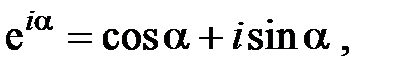
Общее решение для плоской волны в комплексной форме можно записать в ви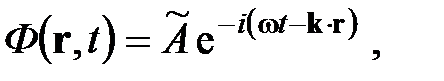де

где 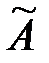– в общем случае комплексная величина, называемая комплексной амплитудой. Тогда учитывая, что

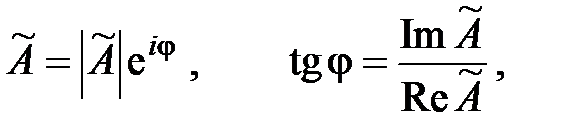
запишем

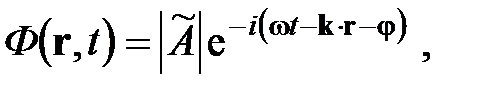
Плоская электромагнитная волна. Для анализа структуры плоской ЭМВ воспользуемся записью уравнений Максвелла с помощью определения и свойств оператора Гамильтона (набла-оператора):

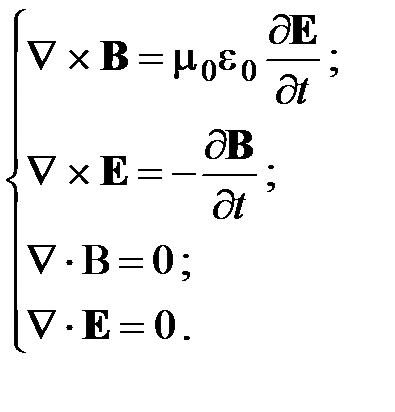
Решение этих уравнений ищем в виде:

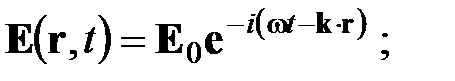
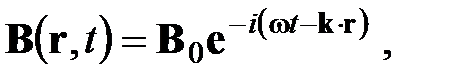
где E ₀ и B ₀ – постоянные векторы, не зависящие от координат и времени (в общем случае компоненты этих векторов могут быть комплексными).

Важные соотношения, описывающие структуру плоской ЭМВ:

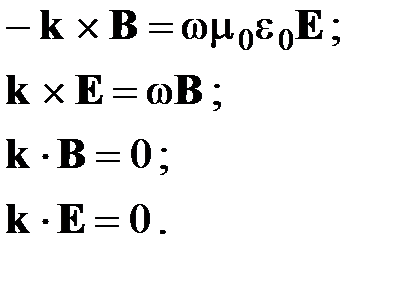
Из этих соотношений можно сделать следующие выводы:

1. Векторы Е и В плоской волны перпендикулярны вектору k, т.е. направлению распространения. Это означает, что плоская ЭМВ является поперечной. E, B и k составляют тройку взаимно перпендикулярных векторов.

2. Соотношение между напряженностью электрического поля и магнитной индукцией плоской ЭМВ в вакууме: E = cB

3. Т.к. k, w, m₀, e₀ – вещественные величины, то это значит, что E и B в плоской ЭМВ колеблются в одинаковой фазе.

Плотность потока энергии электромагнитных волн определяется вектором Пойнтинга:

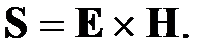
В случае плоской волны модуль вектора Пойнтинга может быть представлен в виде: 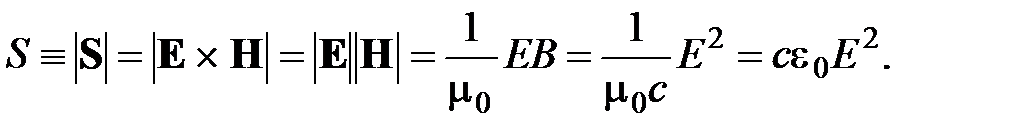При характерных для оптического диапазона высоких частотах w (» 10¹⁵ с^-1) колебания потока энергии волны в каждой точке, происходящие в соответствии с (2.50) на частоте 2w, не наблюдаемы, и физический интерес представляет лишь среднее по времени значение S, называемое обычно интенсивностью света. Учитывая, что E = E₀ cos w t, где E₀ – амплитуда напряженности электрического поля, находим для интенсивности световой волны:

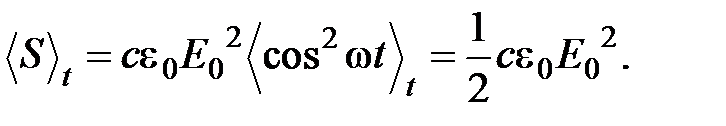
Date: 2015-05-17; view: 797; Нарушение авторских прав