Немонохроматическое излучение

Реальное излучение имеет конечную продолжительность и происходит со случайно изменяющимися амплитудой и фазой. Ограниченность по времени и монохроматичность исключают друг друга. Реальную ЭМВ можно представить в виде наложения монохроматических волн с различными частотами в соответствии с принципом суперпозиции полей. С математической точки зрения спектральный состав излучения анализируется с помощью Фурье–преобразований.

Спектр амплитуд и спектр фаз

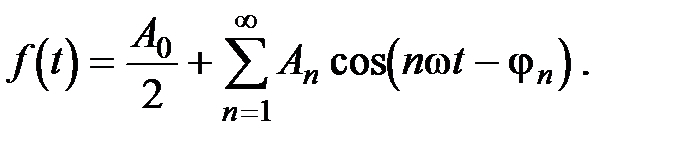
Совокупность A_n называется спектром амплитуд функции f (t), а совокупность j _n – спектром фаз. Частоты по определению имеют положительные значения.

Комплексный спектр (3.8) эквивалентен амплитудному и фазовому спектру

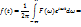
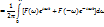
Для вещественной функции f (t) 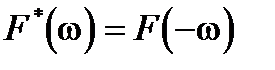и тогда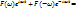

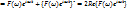
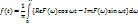
или

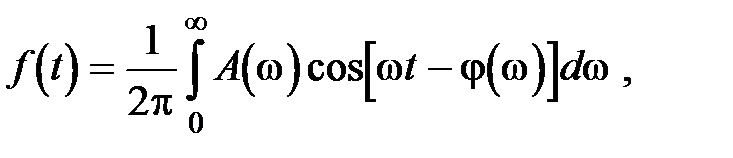
где

Периодические функции характеризуются дискретными спектрами, непериодические – непрерывными.

Продолжительностью (длительностью) импульса называется промежуток времени D t, в течение которого импульс существенно отличается от 0. Шириной спектра называется интервал частот Dn, на котором амплитуда спектра существенно отлична от 0. Вообще говоря, при таком расплывчатом определении универсального соотношения между D t и Dn не существует, но есть универсальная закономерность: ширина спектра обратно пропорциональна продолжительности импульса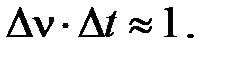

Точное соотношение зависит от формы исследуемого сигнала и от точного определения величин D t и Dn.

Отрицательные частоты. Чаще всего удобнее функцией F (w). Но тогда возникает вопрос о смысле отрицательных частот. F (w) при w > 0 описывает плотность спектральной компоненты частоты w с положительным направлением вращения единичного (базисного) комплексного вектора е ^{i w t}, а F (–w) – плотность спектральной компоненты той же частоты w, но с отрицательным направлением вращения базисного комплексного вектора е^{– i w t}. Таким образом, обращение к отрицательным частотам связано с изменением базисных функций, с помощью которых осуществляется Фурье-преобразование, а именно с переходом к вращающимся комплексным векторам как базисным функциям Фурье-преобразования.

Энергетические спектры. Выразим полную энергию световой волны через интенсивность ее компонент Фурье, вычислив интеграл от E ²(t) по времени:

,

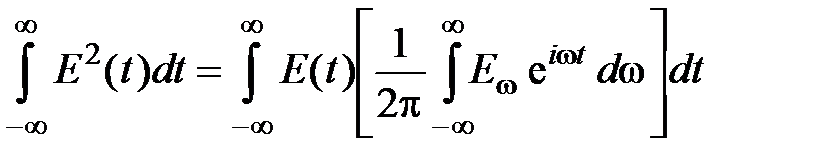где E _w – Фурье-образ поля E (t). Изменяя порядок интегрирования по w и по t, получаем соотношение, называемое теоремой Планшереля:

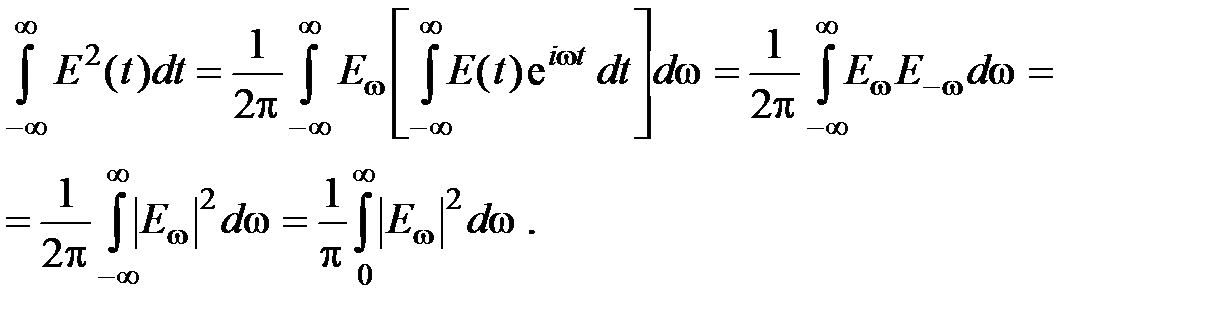Отсюда следует, что полная энергия немонохроматической волны выражается через интеграл по положительным частотам от ее спектральной плотности, характеризующей распределение энергии волны по спектру частот. Отметим, что если E _w полностью определяет поле E (t), то знание спектральной плотности энергии еще не позволяет восстановить функцию E (t). В энергетическом спектре уже не содержится информация о фазовом спектре. Поэтому данное поле E (t) характеризуется вполне определенным спектром, но одному и тому же спектру могут соответствовать различные E (t).

Математическому разложению немонохром. волны в ряд или интеграл Фурье для нахождения спектральной плотности ее энергии можно сопоставить реальный физический процесс ­– экспериментальное измерение спектра такой волны с помощью соответствующего анализатора (спектрального прибора).

Волновые пакеты. В отличие от распространения в вакууме, в среде скорость ЭМВ меньше c = const и зависит от частоты. Зависимость скорости волны от частоты называется дисперсией.

Рассмотрим суперпозицию двух волн:

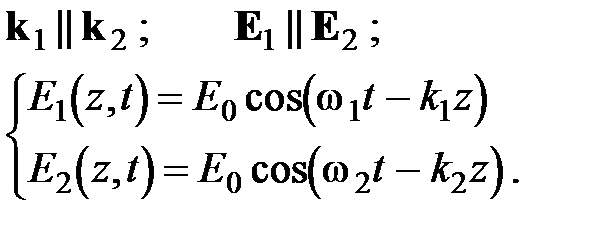
Фазовая скорость определяется из условия: ; .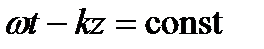

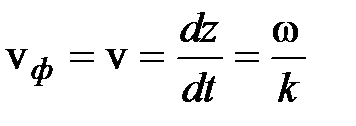Для результирующего поля имеем:

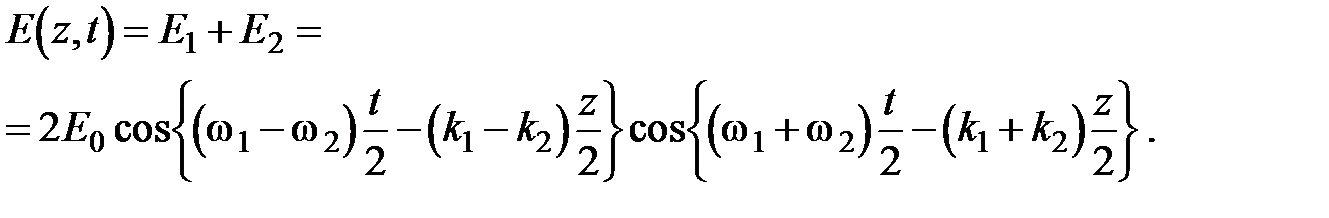Суперпозиция двух и более волн с различными частотами составляет группу волн (волновой пакет). Скоростью группы волн или групповой скоростью u называется скорость движения максимума огибающей амплитуды группы волн:

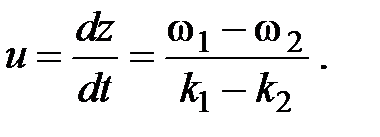
Если дисперсия отсутствует, то u = v. При наличии дисперсии групповая скорость отличается от фазовой. Если 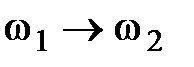, то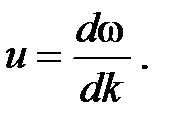

Рассмотрим импульс, состоящий из бесконечно большого числа монохроматических плоских волн, непрерывно заполняющих интервал частот 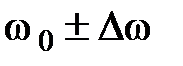, где 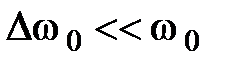. Диапазону частот 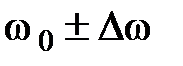соответствует диапазон волновых чисел . Тогда для результирующей напряженности поля имеем:

.

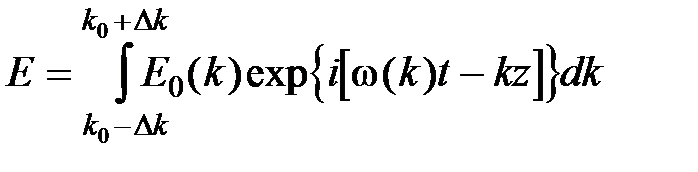(Размерность заключена в амплитуде). Выражение для фазы колебания преобразуем к виду:

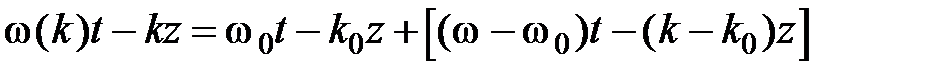Тогда для результирующего поля E получаем:

.

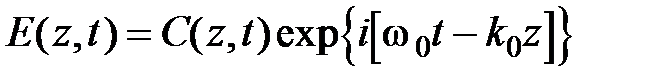Получилось уравнение плоской волны с w₀ и k ₀ и медленно меняющейся в пространстве и во времени амплитудой (огибающей) C (z,t), т.к.

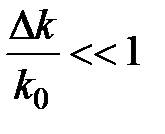и :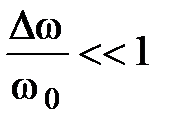

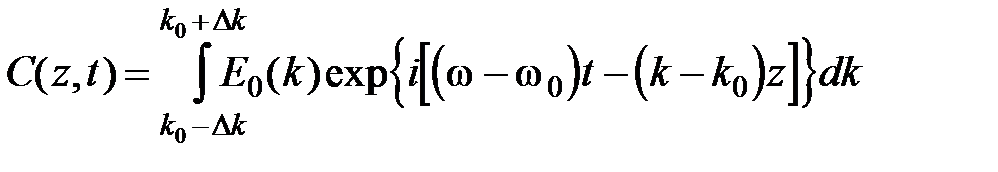Т.к. функция w(k) изменяется в узком интервале волновых чисел вблизи k ₀, то (w – w₀) можно разложить в ряд и ограничиться в разложении первым членом ряда, получаем:

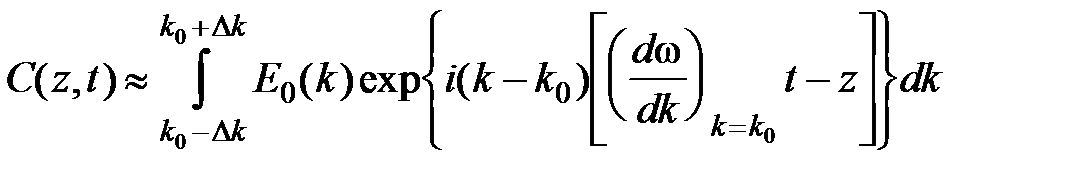В этом приближении C (z,t) представляет собой суперпозицию низкочастотных монохроматических составляющих, распространяющихся с одинаковой скоростью. Зависимость от координат и времени у всех составляющих одинакова, и волновой пакет (импульс) движется как единое целое (не деформируясь) с групповой скоростью 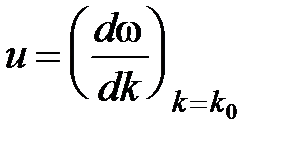. Учет членов более высокого порядка показывает, что форма импульса в процессе распространения изменяется.

Формула Рэлея. Установим связь между групповой и фазовой скоростями.

.

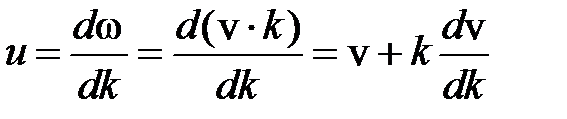Учитывая, что

,

получаем окончательно выражение, называемое формулой Рэлея, позволяющее по заданному закону дисперсии v(l) получить значение групповой скорости:

.

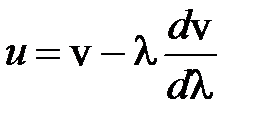5.Оптические явления на границе раздела двух сред.

Граничные условия для векторов поля световой волны на границе между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид:

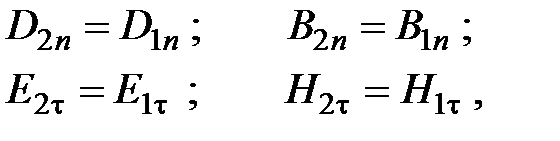
где t, n – индексы тангенциальной (касательной к границе раздела) и нормальной компоненты вектора соответственно.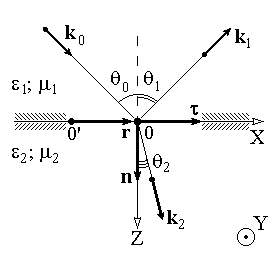

Пусть на плоскую границу двух диэлектриков с абсолютными (не относительными!) проницаемостями (e₁; m₁) и (e₂; m₂) (магнитную проницаемость пока оставим в общем виде) падает под некоторым углом плоская световая волна. Тогда для напряженностей электрического поля в падающей, отраженной и преломленной волнах соответственно имеем:

Где

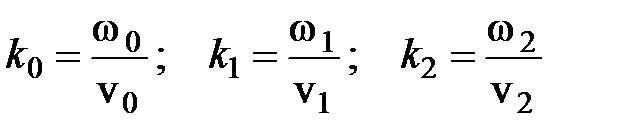
– волновые числа, причем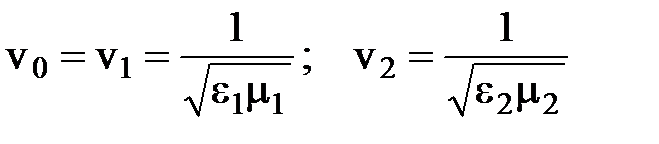

– скорости света в 1-й и 2-й средах.

Законы отражения и преломления света на границе полностью определяются граничными. Для электрического поля граничные условия:

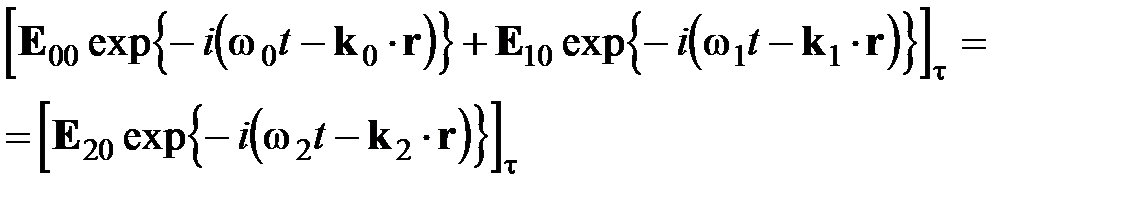Отметим, что начало отсчета вектора r (точка 0’) совершенно произвольно. Если 0’ лежит не на поверхности раздела, то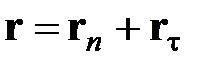

При этом: 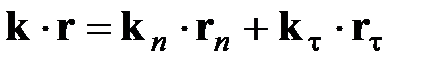. Но для любой точки поверхности 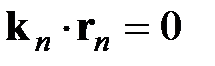, поэтому удобно точку 0’ поместить на границе раздела.

Равенство будет соблюдаться для произвольных значений r и t только при .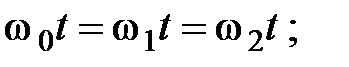

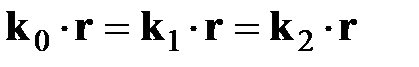Отсюда следует, что .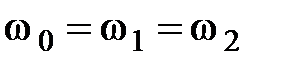

(Частота ЭМВ при отражении и преломлении не меняется.)

Выберем точку 0’ так, чтобы вектор 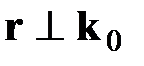(т.е. направим перпендикулярно плоскости XZ). Тогда 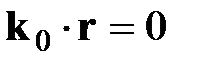, 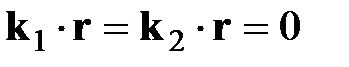. Отсюда следует, что волновые векторы падающей, отраженной и преломленной волн (условно пока назовем направление k лучом) лежат в одной плоскости.

Плоскость, в которой лежат волновой вектор k ₀ и нормаль к поверхности раздела n в точке падения луча, называется плоскостью падения. Из рис. видно, что

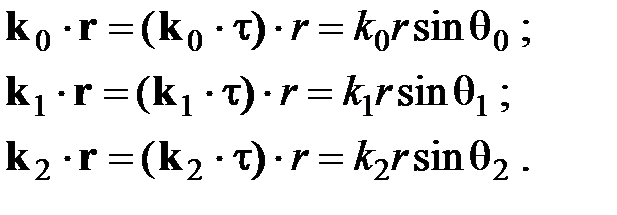
Тогда с учетом (4.31) получаем:

или:

.

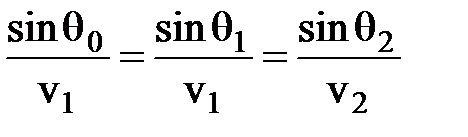Вспомним, что

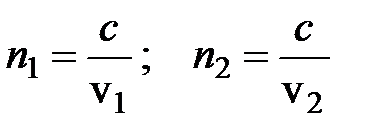– показатели преломления.

; .

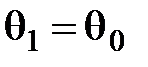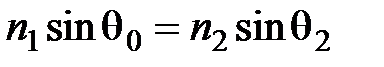(Закон Снеллиуса)

Введем обозначение

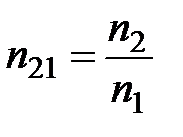– относительный показатель преломления. Тогда закон Снеллиуса примет вид:

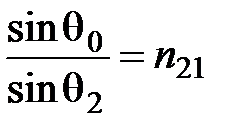
При 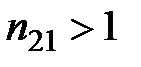(падение из менее оптически плотной в более оптически плотную среду) 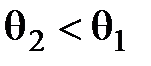. При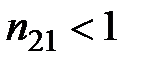

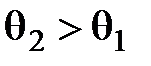
Явление полного внутреннего отражения.

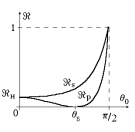
При падении света на границу двух диэлектриков, для которых 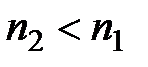, из закона Снеллиуса следует, что существует предельный (или критический) угол q_п падения, при котором угол преломления 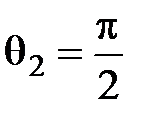. Тогда 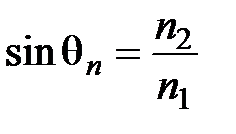. При 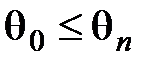угол преломления q₂ имеет обычную геометрическую интерпретацию, и коэффициенты R и T являются вещественными.

Когда угол падения 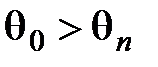, не существует вещественного угла преломления q₂, т.к. закон Снеллиуса дает для sinq₂ значение больше единицы, а для cosq₂ – чисто мнимое значение: 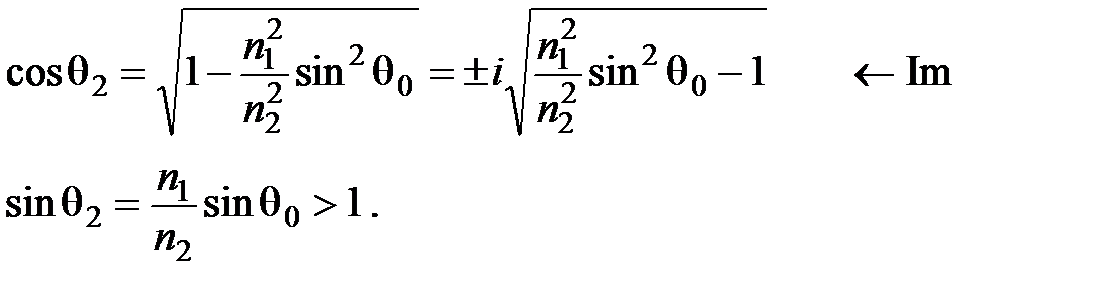Рассмотрим сначала световую волну во второй среде (преломленную) в общем случае:

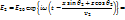
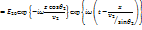
В такой записи сомножитель I означает комплексную амплитуду волны II, распространяющейся вдоль оси X со скоростью :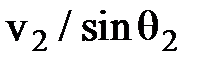

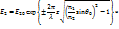
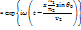
Знак (+) в первой экспоненте соответствует безграничному возрастанию поля в среде, что лишено физического смысла. Поэтому остается(–), что соответствует быстро убывающей с ростом z амплитуде волны, распространяющейся во второй среде вдоль X. Практически эта неоднородная волна существует лишь в поверхностном слое второй среды толщиной порядка длины волны. Причем фазовая скорость этой неоднородной (и соответственно не плоской) зависит как от свойств среды, так и от угла падения.

Формулы Френеля для отраженной волны:

;

.

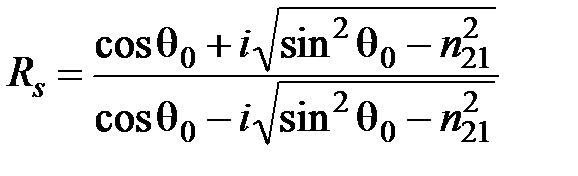Видно, что энергетические коэффициенты 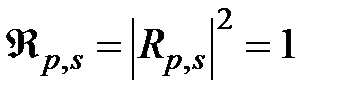при углах падения больше критического. Поэтому это явление называется полным внутренним отражением(ПВО). При этом волна и соответствующая доля энергии проникают через границу раздела во вторую среду на некоторую глубину d (глубину проникновения) (амплитуда поля на глубине d падает в е раз):

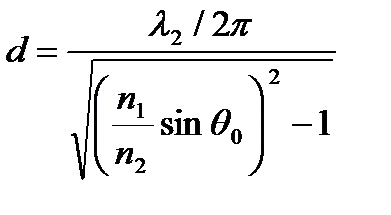, движутся вдоль поверхности раздела и затем возвращаются в первую среду. Места входа энергии во вторую среду и ее возвращения в первую смещены друг относительно друга. Амплитуды p– и s– компонент отраженной волны не изменяются по абсолютному значению, но испытывают различные фазовые сдвиги. Если представить, что

,

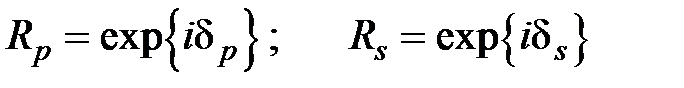то

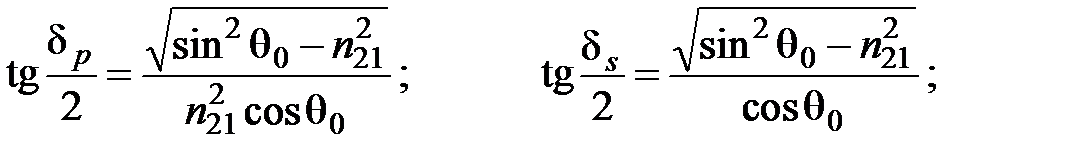
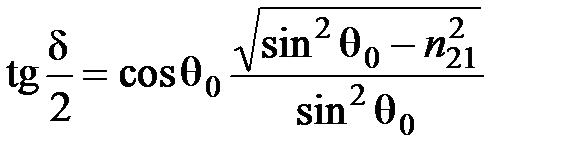
Date: 2015-05-17; view: 1575; Нарушение авторских прав