Спин электрона. Оператор спина электрона. Матрицы Паули. Собственные функции операторов спина

Для полного объяснения всех свойств атома была выдвинута гипотеза о наличии у электрона так называемого спина. Спин — это чисто квантовое свойство электрона, не имеющее классических аналогов. Спин — это собственный момент импульса электрона, не связанный с движением в пространстве. Для полного описания состояния электрона в атоме необходимо к трем квантовым числам n, l, m добавить еще одно - спиновое квантовое число (спин) S. Для всех электронов абсолютное значение спина всегда равно s = ½. Это квантовое число определяет ориентацию собственного момента количества движения электрона на некоторое направление, например, на направление орбитального момента электрона. Наличие спина приводит к удвоению состояний электрона в атоме. Спин не имеет классического аналога, это такое же внутреннее свойство электрона, как его заряд и масса.

Спин – неотъемлемое свойство микрочастицы, особая степень свободы. Для описания этого свойства ему в соответствие приводится механический момент 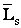. Спиновый (собственный) момент электрона есть вектор 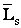, у которого определены только модуль и одна из проекций:

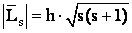(10) (11) где: 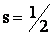(12)(спиновое квантовое число для электрона, принимающее единственное значение ½).

Проекция спина на ось z (магнитное спиновое число m_s) может иметь лишь два значения: (13) (магнитное спиновое квантовое число, принимающее 2 значения).

В соответствии с (12,13) вектор 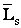для электрона относительно выделенного направления (ось z) может ориентироваться лишь двумя способами (пространственное квантование).

Оператор спина подчиняется тем же соотношениям, что и оператор орбитального момента импульса: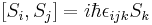

где ε_ijk – символ Леви-Чивиты. Собственные векторы операторов S² и S_z (выраженные через кет-векторы в общем S-базисе) равны:

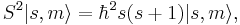
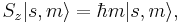
где через m обозначено квантовое число проекции спина на выделенную ось.

Операторы увеличения и уменьшения спина, действующие на данные собственные векторы, дают соотношения:

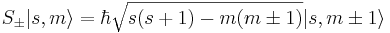, где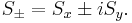

В отличие от орбитального момента импульса, указанные собственные векторы (и соответствующие матричные элементы) не выражаются через сферические гармоники и не являются функциями углов θ и φ. Величины s и m могут быть полуцелыми числами.

В квантовой механике спин квантуется в единицах постоянной Дирака 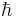, которая образуется путём деления постоянной Планка (постоянной действия) на 2π. При этом функция состояния частицы 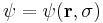зависит как от координат в виде радиус-вектора , так и от 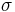в виде дискретного набора величин:

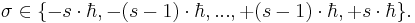
Здесь можно выделить бозоны (s = 0 или 1 или 2 или...) и фермионы (s = 1/2 или 3/2 или 5/2 или...). В процессах взаимодействия сохраняется общий момент импульса системы, складывающийся из орбитального момента импульса и спина.

Date: 2015-05-19; view: 1499; Нарушение авторских прав