
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Центрированные оптические системы
|
|
Прохождение лучей в центрированных оптических системах.
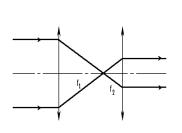
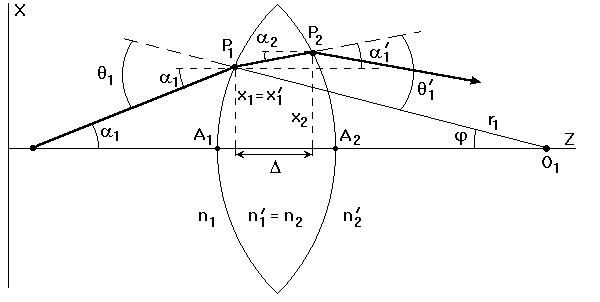 Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину. Ось Z совпадает с осью линзы. Главной оптической осью линзы называется прямая, проходящая через центры кривизны ее поверхности (в данном построении это ось Z). Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. r 1 и r 2 – радиусы кривизны 1-й и 2-й сферических поверхностей линзы. Весь расчет проводится в параксиальном приближении:
Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину. Ось Z совпадает с осью линзы. Главной оптической осью линзы называется прямая, проходящая через центры кривизны ее поверхности (в данном построении это ось Z). Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. r 1 и r 2 – радиусы кривизны 1-й и 2-й сферических поверхностей линзы. Весь расчет проводится в параксиальном приближении:
Преломление на первой сферической поверхности.
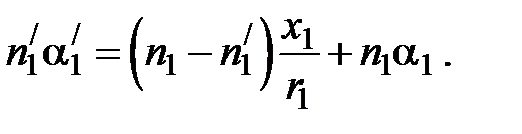
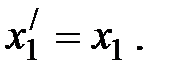
Данная система уравнений получена из закона Снеллиуса и соотношений между углами системы. Систему удобно записать в матричном виде:
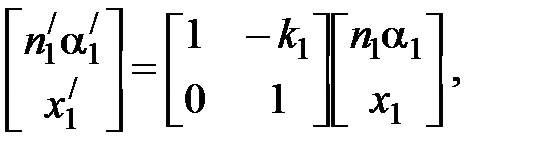
где величина k1= (n1/–n1)/ r 1 называется преломляющей силой первой поверхности, а матрица
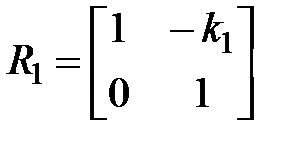
называется преломляющей матрицей первой поверхности.
Распространение луча внутри линзы. Преломленный луч в параксиальном приближении, пройдя внутри линзы, падает на её вторую поверхность на расстоянии x 2 от оси:
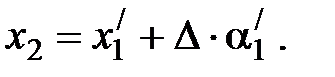
Отметим, что величина D в параксиальном приближении практически равна толщине линзы А1А2. Получаем в матричном виде:
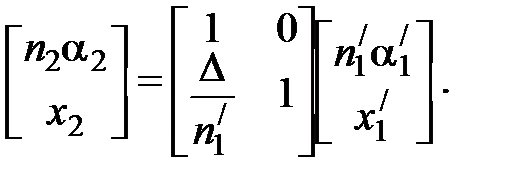
Матрица
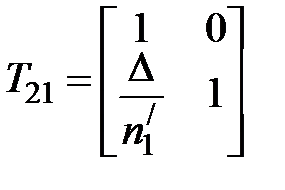
описывает распространение луча от первой поверхности линзы ко второй и называется передаточной матрицей.
Преломление луча на второй сферической поверхности рассматривается точно так же, как и на первой поверхности. Величина k2= (n2/ –n2)/ r 2 называется преломляющей силой второй поверхности, а матрица R2 – преломляющей матрицей второй поверхности:
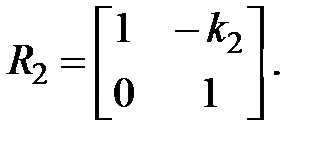
Знаки всех величин в приведенных выражениях необходимо брать с учётом правила знаков: если встречаемая лучом преломляющая поверхность выпуклая, то её радиус кривизны надо брать с положительным знаком, а если вогнутая – с отрицательным; углы a, отсчитываемые от оси Z против часовой стрелки, положительны, а по часовой стрелке – отрицательны; расстояния, отсчитываемые по Z (по рис. 5.3 – слева направо), положительны, а против Z (справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх, положительны, вниз – отрицательны.
Распространение луча через оптическую систему. Связь между характеристиками на выходе линзы и входе в неё:
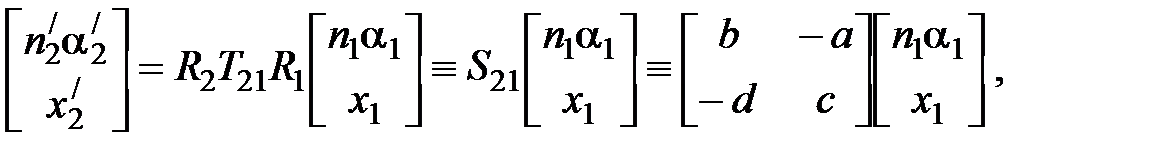
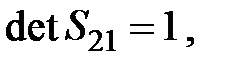
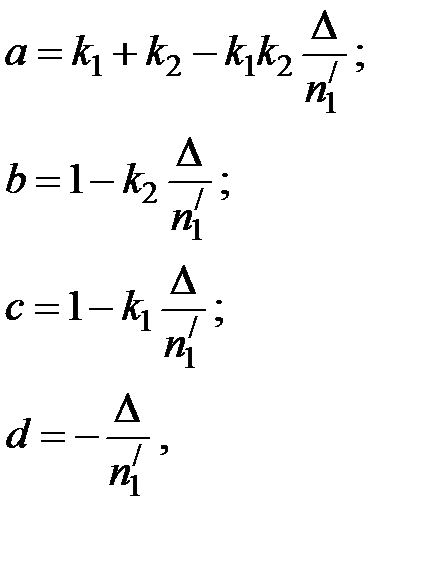
где a, b, c, d называются постоянными Гаусса. Независимыми являются только три из четырех постоянных Гаусса. Матрица S 21 полностью описывает рассмотренную оптическую систему.
Преобразование луча от плоскости предмета к плоскости изображения. Пусть из точки некоторой плоскости (плоскости предмета), расположенной на расстоянии l слева от точки А 1 выходит луч с координатами (n1 a 1, x) и падает на рассматриваемую линзу. В некоторой плоскости, расположенной справа от точки А 2 на расстоянии l / луч характеризуется координатами (n2/ a 2/, x /). Связь между параметрами системы:
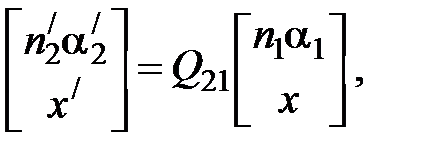
Матрица Q21 называется матрицей преобразования предмета к изображению:
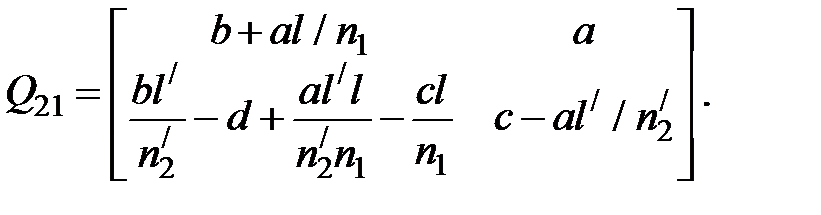 Обозначим
Обозначим 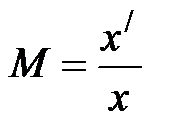 – увеличение оптической системы. Под изображением понимается такое отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, исходящие от точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением.
– увеличение оптической системы. Под изображением понимается такое отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, исходящие от точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением.
Исходя из этого определения в точке изображения увеличение М не должно зависеть от угла a1
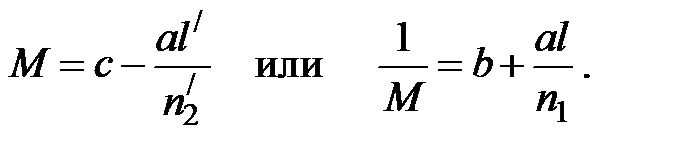
Тогда матрица преобразования от предмета к изображению принимает вид:
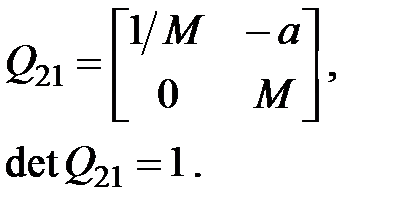
Кардинальные элементы оптической системы. Плоскости H и H /, увеличение для точек которых М = 1, называются главными плоскостями, а их пересечения с осью системы (ось Z) – главными точками системы. Их положение:
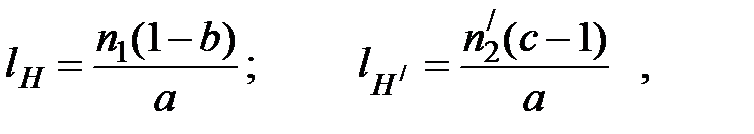 где l H – отсчёт положения плоскости H относительно точки А 1; l H/ – отсчёт положения плоскости H относительно точки А 2 .
где l H – отсчёт положения плоскости H относительно точки А 1; l H/ – отсчёт положения плоскости H относительно точки А 2 .
Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно оптической оси (т.е. точка с увеличением M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с увеличением M = ¥), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Их положение:
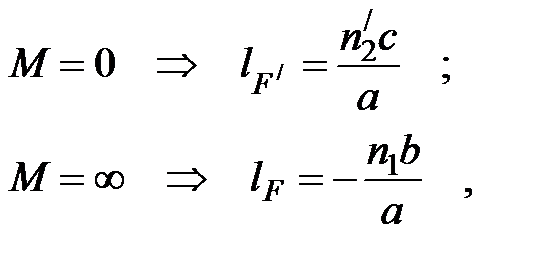
где lF – отсчёт положения переднего фокуса относительно точки А 1, l F/ – отсчёт положения заднего фокуса относительно точки А 2.
Расстояние f между передним фокусом и передней главной точкой называется передним фокусным расстоянием; расстояние f / между задним фокусом и задней главной точкой называется задним фокусным расстоянием:
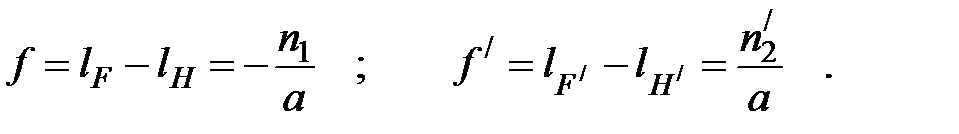 Главные и фокальные плоскости называются кардинальными элементами оптической системы
Главные и фокальные плоскости называются кардинальными элементами оптической системы
Физический смысл постоянных Гаусса. Пусть линза располагается в воздухе: n 1 = n 2/ = 1. Тогда:
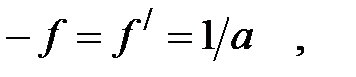 т.е. a является величиной, обратной фокусному расстоянию.
т.е. a является величиной, обратной фокусному расстоянию.
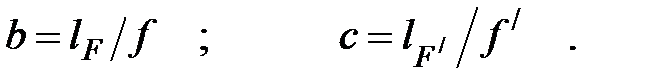
Коэффициенты b и c характеризуют взаимное расположение главных и фокальных плоскостей.
Уравнение линзы. У равнение линзы в форме Ньютона:
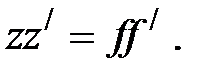
Уравнение линзы в форме Гаусса:
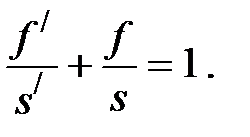
Увеличение линзы определяется из формулы:
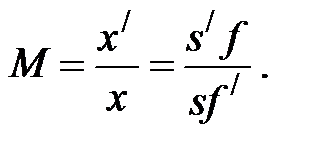
Тонкие линзы. Пусть 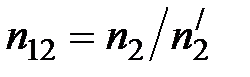 – относительный коэффициент преломления и
– относительный коэффициент преломления и 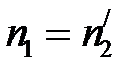 . Для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:
. Для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:
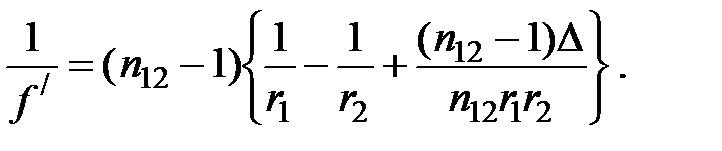 (1)
(1)
Тонкой линзой называется линза, для которой можно пренебречь третьим слагаемым в скобках (1), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:
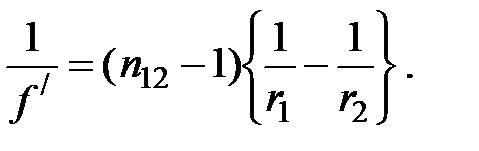
Тонкая линза представляется не имеющей толщины и с ней совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:
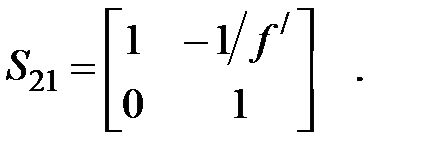
Величина
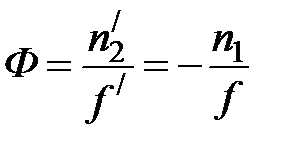
называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.
Отражение от сферических поверхностей рассматривается как преломление в среду с отрицательным показателем преломления – n, если n – показатель преломления среды, из которой луч падает на отражающую поверхность. В остальном матрица, описывающая отражение, полностью аналогична матрице, описывающей преломление. Правило знаков остается тем же.
Аберрации оптических систем. Отклонения фактически получаемого изображения от идеального, описываемого всеми предыдущими формулами, называются аберрациями. Для параксиальных лучей аберрации малы и ими пренебрегают. Если же лучи не параксиальны, то аберрации становятся значительными и сильно искажают изображение.
Первый источник аберраций состоит в том, что линзы, ограниченные сферическими поверхностями, преломляют лучи не совсем так, как это принимается в параксиальном. Такие аберрации называются геометрическими.
К геометрическим аберрациям относятся: сферическая аберрация, кома, астигматизм, искривление поверхности изображения (кривизна поля), дисторсия.
При сферической аберрации лучи, параллельные оптической оси, не пересекаются после линзы в одной точке. Пучок параллельных оси лучей после преломления образует совокупность конусов, вершины которых расположены на оси. Огибающая эту совокупность конусов поверхность называется каустической, а сечение этой поверхности любой плоскостью, проходящей через луч – каустической кривой
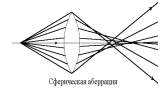
Если светящаяся точка расположена не на оптической оси, то её изображение не является светящимся кружком, как в предыдущем случае, а представляется в виде довольно сложной асимметричной фигуры, напоминающей комету с хвостом. Такая аберрация называется комой.
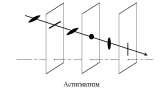
Если на линзу падает цилиндрический пучок лучей под достаточно большим углом к оптической оси, то в результате сечение пучка лучей изменяется с расстоянием от линзы после преломления. На некотором расстоянии от линзы сечение является отрезком линии, перпендикулярным плоскости падения пучка (такая плоскость падения, образованная осью падения пучка и оптической осью, называется меридианальной плоскостью, а перпендикулярная ей – сагиттальной). Затем эта линия переходит в эллипс, на некотором расстоянии дальше сечение опять становится круговым, а затем эллиптическим и дальше превращается в отрезок линии, лежащей в меридианальной плоскости. Такой вид аберрации называется астигматизмом.
Поверхности, на которых лежат фокусы (где образуются отрезки линий при астигматизме), создаваемые меридианальной и сагиттальной фокусировками, не совпадают между собой и не являются плоскостями. Эти поверхности касаются лишь в точке F/ оптической оси. Этот вид аберрации называется искривлением поверхности изображения.
Увеличение системы, вообще говоря, зависит от угла наклона падающих лучей. В результате, например, сетка из прямых линий превращается в сетку из кривых линий. Такая аберрация называется дисторсией.
Второй источник аберраций связан с дисперсией света. Т.к. показатель преломления зависит от частоты, то и фокусное расстояние и другие характеристики системы зависят от частоты. Поэтому лучи, соответствующие излучению различной частоты, исходящие из одной точки предмета, не сходятся в одной точке изображения даже в идеальном случае. Такие аберрации называются хроматическими.
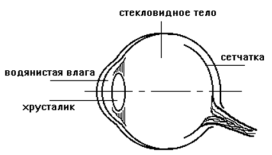
Некоторые приборы геометрической оптики. 1. Глаз
. 
2. Линзовый телескоп Увеличение
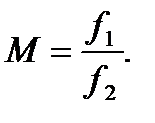
3. Лупа. Простейшая оптическая система с малым фокусным расстоянием (~1 см или немного больше). Предмет располагается на расстоянии от лупы меньше фокусного. Изображение мнимое, прямое, увеличенное. Увеличение
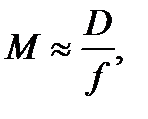 где D – расстояние наилучшего зрения (25 см).
где D – расстояние наилучшего зрения (25 см).
9 .Интерференция света.
Под интерференцией изменение средней плотности потока энергии, обусловленное суперпозицией электромагнитных волн.
В дальнейшем под интенсивностью световой монохроматической волны будем понимать следующую величину, определяемую формулой:

где E 0 – действительная амплитуда световой волны.
Рассмотрим суперпозицию двух линейно поляризованных в одном направлении волн с различными амплитудами:
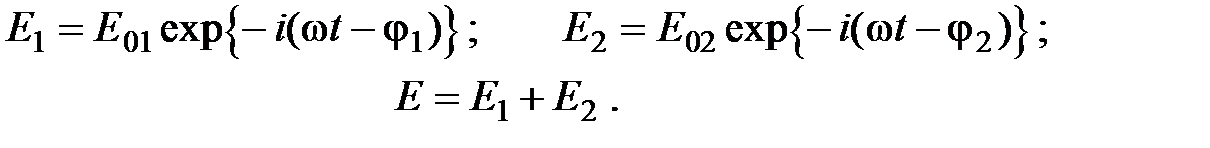 Тогда суммарная интенсивность I будет равна:
Тогда суммарная интенсивность I будет равна:
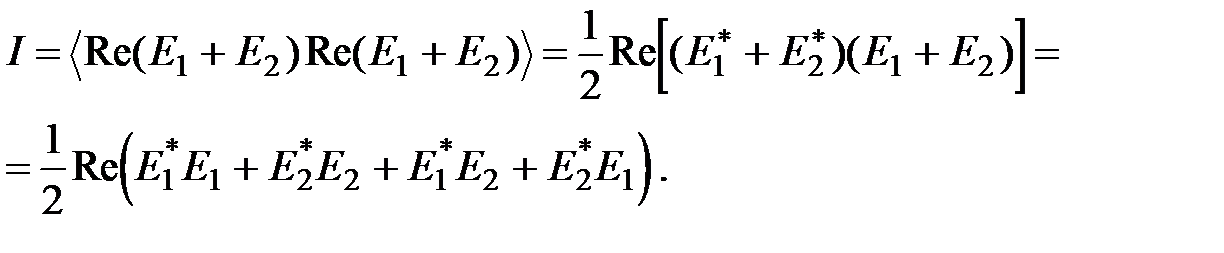
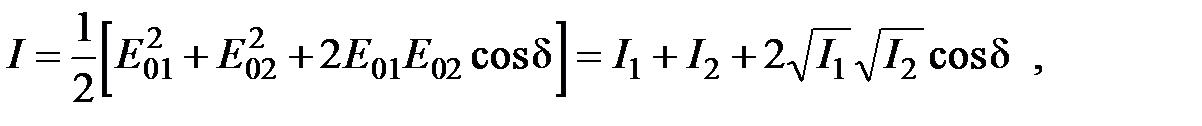 где
где 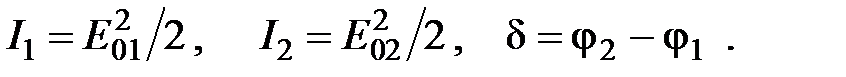
Если частоты интерферирующих волн различны, то:
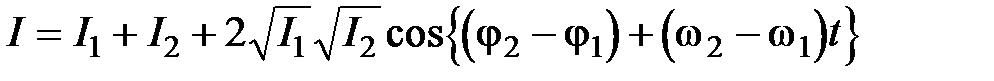 Последнее слагаемое называется интерференционным членом. В тех случаях, когда он обращается в нуль, результирующая интенсивность равна сумме интенсивностей отдельных волн и интерференция отсутствует. Если же интерференционный член отличен от нуля, то суммарная интенсивность изменяется от минимального значения
Последнее слагаемое называется интерференционным членом. В тех случаях, когда он обращается в нуль, результирующая интенсивность равна сумме интенсивностей отдельных волн и интерференция отсутствует. Если же интерференционный член отличен от нуля, то суммарная интенсивность изменяется от минимального значения
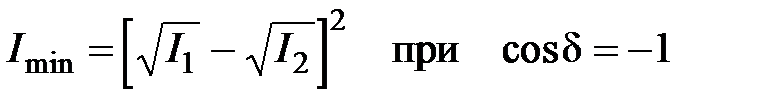
до максимального значения
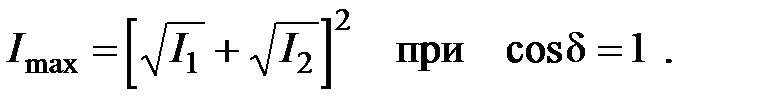
Монохроматических волн в природе не существует, поэтому приходится ограничиться квазимонохроматическими волнами. Картина интерференции монохроматических волн является лишь первым приближением в интерференции волн от реальных источников. Существующие экспериментальные методы получения интерференционной картины обычно делятся на два класса: 1) способы деления амплитуды волны; 2) способы деления фронта волны.
Интерферометр Майкельсона. Интерферометр состоит из делительной пластинки P и двух зеркал R 1 и R 2, расположенных на расстояниях l 1 и l 1 от пластины. На пластинке P происходит деление амплитуды, поскольку фронты волн на ней сохраняются, меняя лишь направление своего движения. Нетрудно показать, что при любом коэффициенте отражения света от пластинки амплитуды полей, приходящих в точку наблюдения А одинаковы. Т.к. частоты также остаются постоянными, то:
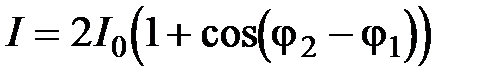 .
.
При этом интенсивность I изменяется от своего минимального значения при 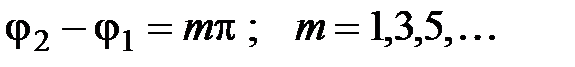 до своего максимального значения при
до своего максимального значения при 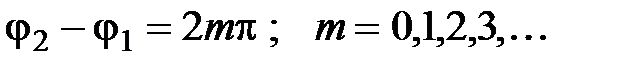 . Значение разности фаз определяется длинами плеч интерферометра l 1 и l 2:
. Значение разности фаз определяется длинами плеч интерферометра l 1 и l 2:
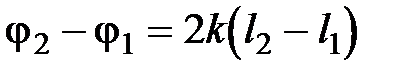 .
.
Пример применения интерферометра Майкельсона.При движении одного из зеркал за счет продольного эффекта Доплера происходит смещение частоты отраженной волны:
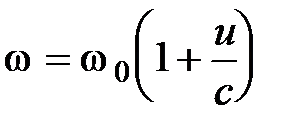 .
.
Тогда существенной станет не постоянная амплитуда, а периодически изменяющаяся с частотой в соответствии со значением скорости движения зеркала:
 .
.
Как видно, интерферометр Майкельсона – прекрасный инструмент не только для измерений расстояний, но и скорости перемещения объектов, т.к. он весьма чувствителен к перемещениям.
Поставив в одно из плеч призму или линзу, можно получить великолепный инструмент для исследования их качества по интерференционной картине (интерферометр Тваймана–Грина).
Другой пример интерферометра по методу деления амплитуды – интерферометр Маха–Цендера. По изменению интерференционной картины и длине пути светового пучка в ячейке Q можно с большой точностью определить относительный показатель преломления исследуемого вещества ячейки.
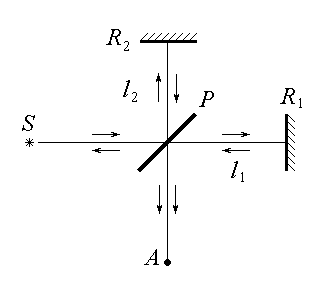
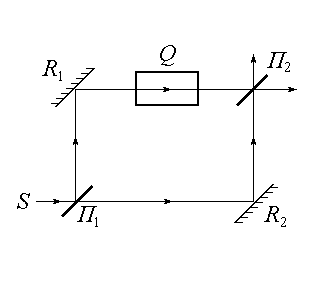
Майкельсон Мах-Цендер
Принцип Гюйгенса. Если в некоторый момент времени задан фронт световой волны, то для определения положения фронта через промежуток времени D t надо каждую точку фронта рассматривать как вторичный источник сферической волны. Поверхность, огибающая вторичные сферические волны радиусом с D t, представляет фронт волны через промежуток времени D t. При анализе распространения волн необходимо учитывать фазу и амплитуду интерферирующих вторичных волн.
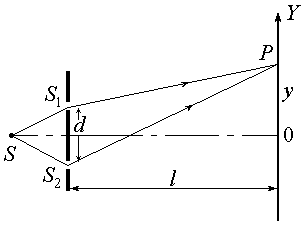
Опыт Юнга. (1801 г.) Рассмотрим интерференцию, возникающую в результате выделения с помощью двух щелей S 1 и S 2 участков сферического волнового фронта волны от точечного источника S (метод деления волнового фронта). Найдем разность хода лучей в произвольной точке наблюдения P на экране:
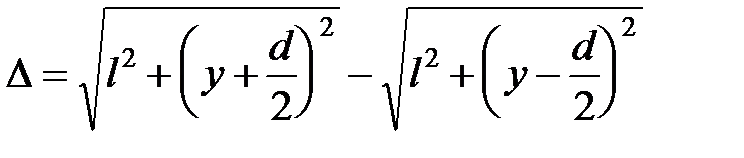
При 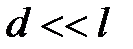 (что обычно реализуется в эксперименте) получаем:
(что обычно реализуется в эксперименте) получаем:
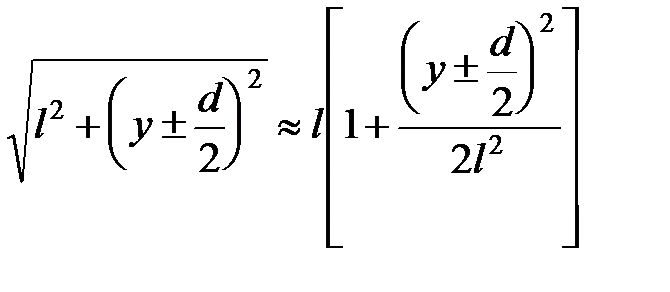 .
.
Следовательно, с точностью до величины первого порядка по 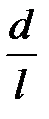 имеем:
имеем:
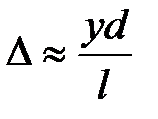 .
.
Разность фаз между волнами в точке наблюдения при этом равна:
 .
.
Интерференционная картина на экране в зависимости от координаты y принимает вид:
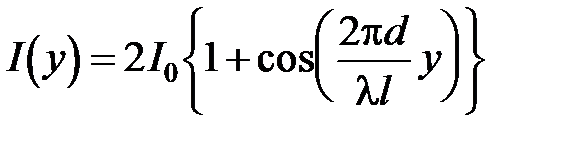
Разумеется, приведенный расчет весьма приблизительный, т.к. кроме используемого приближения мы не учитывали размеры отверстия, а в их пределах фаза может существенно изменяться. Если же размеры меньше длины волны, то необходимо учитывать дифракционные эффекты.
11. Многолучевая интерференция.
Многолучевая интерференция. Рассмотрим многолучевую интерференцию на примере интерферометра Фабри–Перо (ИФП)
Исследуем сначала интерференцию многих световых волн при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку толщиной h и показателем преломления n. Обозначим {T,R}– амплитудные коэффициенты пропускания и отражения при входе волны внутрь пластины, {T’,R’}– амплитудные коэффициенты пропускания и отражения на выходе волны из пластины наружу. При этом справедливы соотношения:
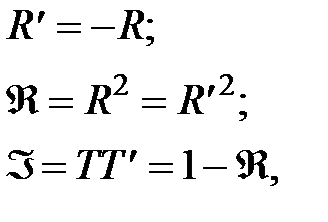
где Á и Â – энергетические коэффициенты пропускания и отражения соответственно. Будем считать углы падения j и преломления q достаточно малыми, что можно считать коэффициенты отражения и пропускания независящими от этих углов. Разность хода D между соседними интерферирующими волнами на выходе пластины равна 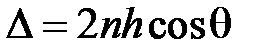 ,
,
а разность фаз равна 
Суммарная амплитуда E 2 прошедшей волны определяется суперпозицией всех прошедших пластинку волн:
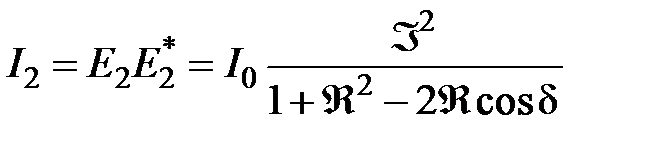
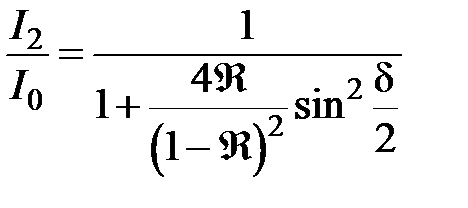
Эта формула носит название формулы Эйри.
Отметим, что аналогично можно найти суммарную интенсивность света при отражении от плоскопараллельной пластинки:
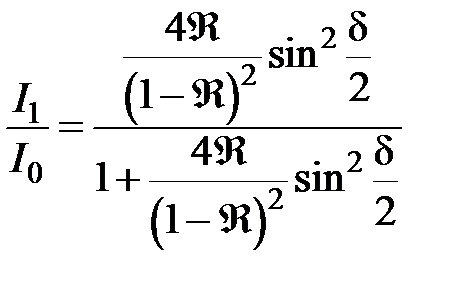 .
.
Интерференционные картины в проходящем и отраженном свете оказываются дополнительными.
Максимумы функции 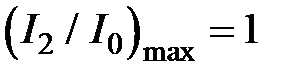 достигаются при
достигаются при 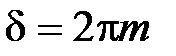 , где m = 0,1,2,..., а минимумы
, где m = 0,1,2,..., а минимумы 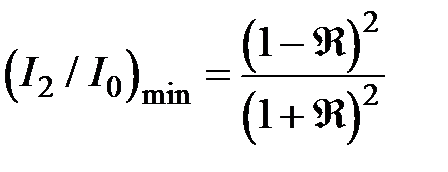 – при
– при 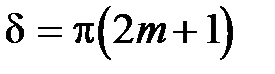 . Т.о. функция видности интерференционной картины равна:
. Т.о. функция видности интерференционной картины равна:
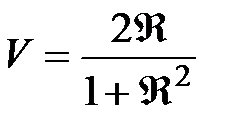 ,
,
т.е. при Â ® 1 Þ V ® 1. При минимуме прошедшей проинтерферировавшей волны наблюдается максимальное отражение света от интерферометра тоже за счет интерференционного сложения волн на зеркалах.
Если на ИФП падают пучки света под всевозможными углами, то интерференционные полосы имеют вид колец. Максимальный порядок интерференции соответствует центру интерференционной картины. Интерференционная картина имеет одинаковый вид там, где падающие пучки имеют одинаковый угол падения на ИФП (полосы равного наклона). Интерференционная картина наблюдается или на бесконечности, или (что обычно реализуется в эксперименте) в фокальной плоскости линзы.
Интерферометр с показателем преломления между зеркалами n = 1 называется эталоном Фабри–Перо).
Разрешающая способность интерферометра Фабри–Перо. Пусть на ИФП падают две волны с близкими длинами l и l+Dl. Каждая из них создает свою интерференционную картину. При достаточно близких длинах волн возникает проблема разрешения (различения) этих двух длин волн по наложенным интерференционным картинам. Разрешающая способность интерферометра g характеризуется минимальной разницей Dl в длинах волн, при которой возможно их разрешение:
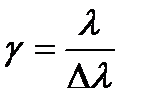 .
.
В теории ИФП принимается, что условием разрешения является пересечение кривых, описывающих распределение интенсивности от каждой из волн на половине их максимального значения, т.е. где 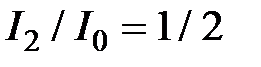 . Ширина линии на полувысоте:
. Ширина линии на полувысоте:
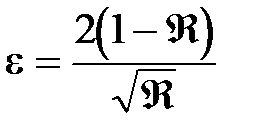 .
.
Для эталона Фабри–Перо при достаточно больших коэффициентах отражения от пластин получаем значение разрешающей способности:
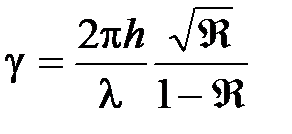 .
.
Отсюда видно, что с увеличением Â разрешающая способность ИФП повышается. Также приводит к увеличению разрешающей способности и увеличение расстояния между пластинами h. Но добиться сколь угодно большой разрешающей способности препятствуют ряд факторов.
Факторы, ограничивающие разрешающую способность:
1.Пластины ИФП не могут быть сделаны абсолютно плоскими.
2.Необходимо добиться параллельности пластин с той же точностью, что и для их плоскостности.
3.Расстояние между пластинами, умноженное на число эффективных отражений, должно быть меньше, чем длина временной когерентности исследуемого света.
Дисперсионная область. При увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью (или областью свободной дисперсии) G. Из определения дисперсионной области следует:
 .
.
Отсюда получаем:
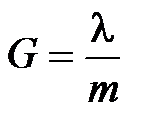 .
.
Для ИФП при 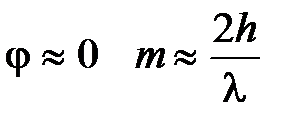 , поэтому дисперсионная область равна:
, поэтому дисперсионная область равна:
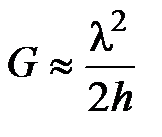 .
.
Из сравнения формул для разрешающей способности и дисперсионной области видно, что требование повышения обеих этих величин противоречат друг другу. Для повышения разрешающей способности приходится работать на больших порядках интерференции, т.е. там, где мала дисперсионная область.
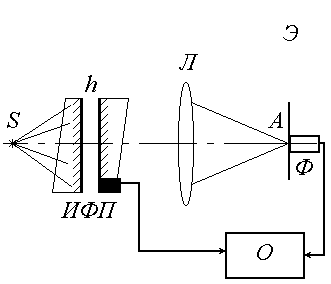
 Сканирующий интерферометр Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.8), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия
Сканирующий интерферометр Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол j, то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.8), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия 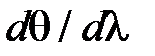 в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+ v t. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию. При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины
в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+ v t. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию. При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины 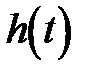 электрическим сигналом.
электрическим сигналом.
12. Дифракция света.
 Под дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой. В явлениях дифракции, как и в интерференции, проявляются волновые свойства света.
Под дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой. В явлениях дифракции, как и в интерференции, проявляются волновые свойства света.
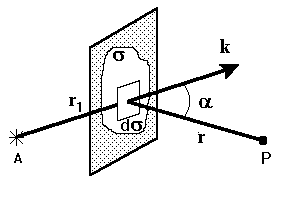
Пусть A – источник света, а s – произвольная замкнутая поверхность, охватывающая A. Принцип Гюйгенса – Френеля: в любой точке, находящейся вне поверхности s, световая волна, возбуждаемая источником A, может быть представлена как результат суперпозиции когерентных вторичных волн, которые “излучаются” элементарными воображаемыми источниками, непрерывно распределенными вдоль вспомогательной поверхности s. Рассмотрим экран с некоторым отверстием, через которое проходит свет от данного источника A. Проведем мысленно произвольную поверхность s, закрывающую отверстие в экране и ограниченную краями отверстия. Разделим эту поверхность на элементарные участки площадью ds, малые по сравнению с размерами отверстия, но большие по сравнению с длиной волны. Каждый из этих участков сам становится источником вторичных волн, распространяющихся во все стороны. Пусть E (r 1) – напряженность поля в самом участке ds. Напряженность поля d E p, создаваемая элементарным участком ds в точке наблюдения P определяется формулой:
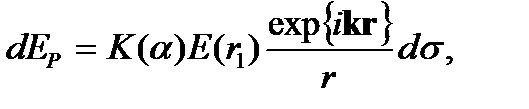
где K (a) – некоторый коэффициент, учитывающий зависимость амплитуды вторичных волн от угла a между вектором k и направлением на точку наблюдения. Полное поле в точке P представляет собой суперпозицию полей от всех элементов ds поверхности, закрывающей отверстие в экране:
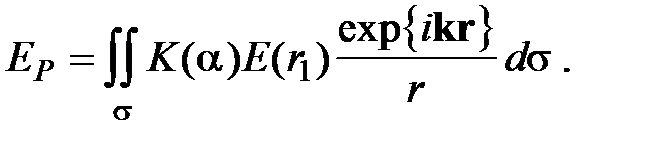
Эта формула дает математическое выражение принципа Гюйгенса – Френеля.
Зоны Френеля. Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения:
1.непроницаемые части экрана не являются источниками вторичных волн; 2.в отверстии точки волнового фронта являются такими же источниками вторичных волн, какими они были бы при отсутствии непроницаемых частей экрана.
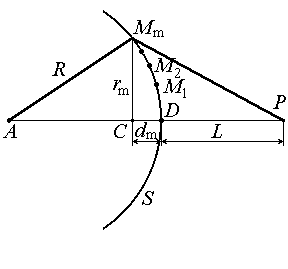
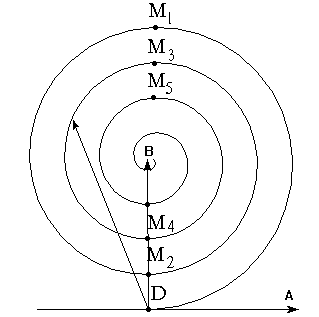
Пусть A – источник сферической волны, S – волновой фронт в некоторый момент времени, R – радиус кривизны этого фронта. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M 1, M 2, M 3 , …) до P отличались на l/2 (эти зоны называются зонами Френеля):
Из геометрии рис. можно получить для радиуса m –й зоны Френеля rm:
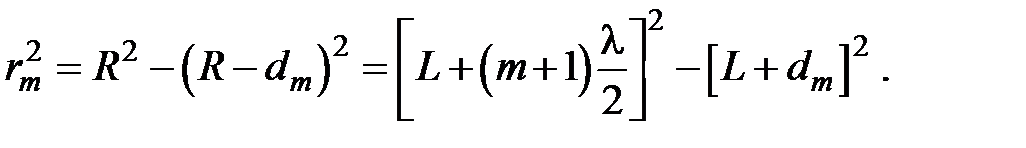 Исключая величину d m и пренебрегая слагаемыми ~l2 ввиду их малости, получаем:
Исключая величину d m и пренебрегая слагаемыми ~l2 ввиду их малости, получаем:
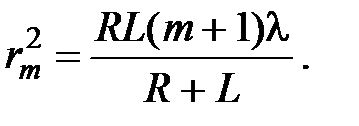
Площади всех зон Френеля примерно одинаковы (в случае пренебрежения кривизной поверхности, что не вносит существенной ошибки, если радиусы зон Френеля много меньше радиуса кривизны волнового фронта (обычно это справедливо для очень большого числа зон Френеля)):
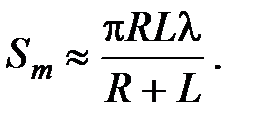
Графическое вычисление амплитуды (метод векторных диаграмм). Разделим каждую из зон на большое число N участков. Между началом и концом зоны фаза меняется на p, а между малыми участками – на d = p/ N. Пусть E 0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна:
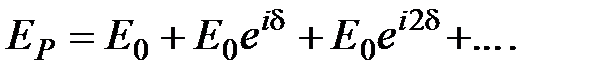
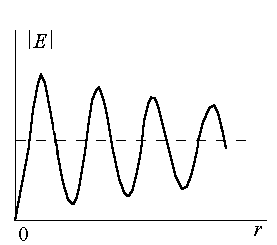
Аналитическое сложение амплитуд можно проделать графически, изображая комплексную амплитуду в виде вектора. При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM 1 пропорциональна амплитуде волны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции гаси ли бы друг друга, но коэффициент наклона K (a) убывает по мере увеличения a и приводит к уменьшению амплитуд вторичных волн. Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана
Пятно Пуассона. Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Необходимость возникновения светлого пятна очевидна из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности.
Отметим, что можно наблюдать и противоположный эффект – темное пятно в центре картинки при дифракции на открытом отверстии. Такое пятно называется пятном Араго.
Трудности метода зон Френеля. Метод зон Френеля приводит к результатам, которые хорошо согласуются с экспериментом для практически важных случаев, когда размеры препятствий много больше длины волны. Однако метод имеет существенные недостатки:
Он не решает вопроса о законе ослабления амплитуды вторичных волн в зависимости от направления распространения. Эту зависимость приходится постулировать.
Метод Френеля дает неправильную фазу волны.
13. Дифракция света.
Под дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой.
Приближение Кирхгофа.
Рассмотрим монохроматическую волну
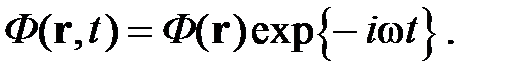
Подставляя это выражение в волновое уравнение, получим для пространственно зависящей амплитуды:
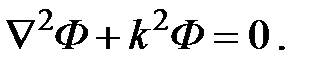
При 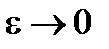 имеем:
имеем:
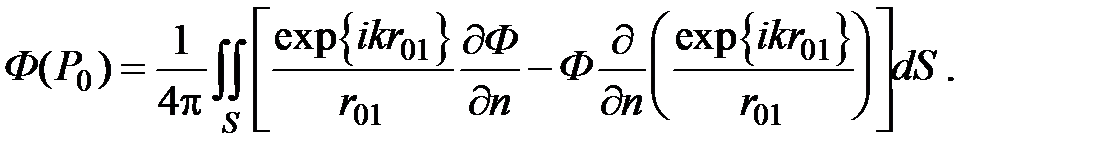 Это интегральное уравнение называется интегральной теоремой Гельмгольца-Кирхгофа и является основой скалярной теории дифракции. Она позволяет вычислить значение функции Ф в любой точке внутри объема, если известны значения функции и ее производной по нормали на поверхности, ограничивающей этот объем.
Это интегральное уравнение называется интегральной теоремой Гельмгольца-Кирхгофа и является основой скалярной теории дифракции. Она позволяет вычислить значение функции Ф в любой точке внутри объема, если известны значения функции и ее производной по нормали на поверхности, ограничивающей этот объем.
Для того чтобы формулу использовать не как интегральное уравнение для Ф, а как формулу для вычисления Ф(P0) (P0 – фиксированная точка внутри этого объема) по известным значениям этой функции и ее производной в точках плоского экрана, Кирхгоф предложил следующие правила для определения их значений в плоскости экрана (приближение Кирхгофа): 1.На отверстиях Ф и ¶Ф/¶n имеют те же значения, какие они имели бы при отсутствии непрозрачных частей экрана. 2.На непрозрачных частях экрана Ф = 0 и ¶Ф/¶n = 0.
Выбор граничных условий в соответствии с этими правилами приводит к решению задач дифракции в приближении Кирхгофа. Граничные условия Кирхгофа никогда точно не выполняются, т.к.: на краях отверстий должны соблюдаться определенные граничные условия, которые можно найти в соответствии с электромагнитной теорией света; за экраном не может быть резкой тени, т.е. скачкообразного обращения Ф в нуль.
Приближение Кирхгофа хорошо работает при линейных размерах отверстий (или экранов) много больших длины волны.
Оптическое приближение. В видимом диапазоне как правило соблюдается условие:
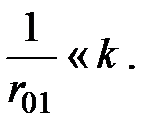
При его выполнении:
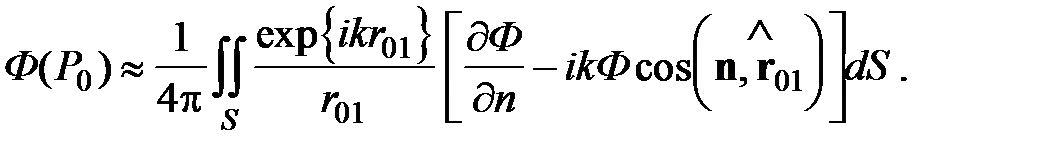
Формула дифракции Френеля-Кирхгофа. Пусть на отверстие падает сферическая волна, исходящая из точки P2:
В оптическом приближении:
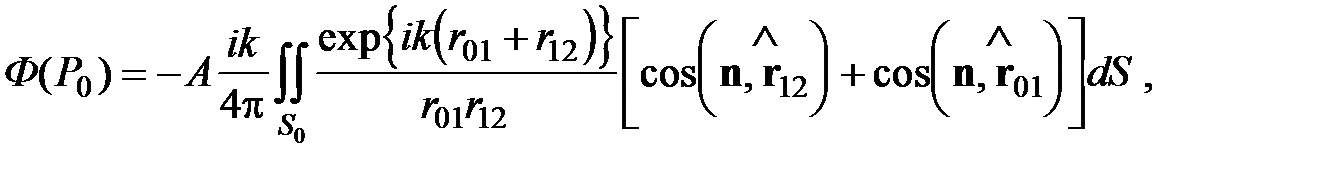 где S0 – площадь отверстия. (На непрозрачных частях экрана подынтегральное выражение равно нулю.) - формула дифракции Френеля-Кирхгофа.
где S0 – площадь отверстия. (На непрозрачных частях экрана подынтегральное выражение равно нулю.) - формула дифракции Френеля-Кирхгофа.
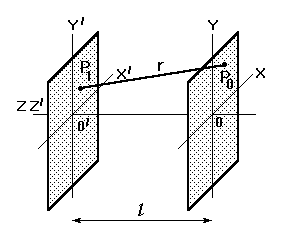 Приближение Френеля. Пусть дифракционная картина наблюдается в плоскости (плоскости дифракционной картины), параллельной экрану с отверстиями (плоскости источников), l – расстояние между этими плоскостями. В каждой плоскости введем системы координат P0 точка наблюдения.
Приближение Френеля. Пусть дифракционная картина наблюдается в плоскости (плоскости дифракционной картины), параллельной экрану с отверстиями (плоскости источников), l – расстояние между этими плоскостями. В каждой плоскости введем системы координат P0 точка наблюдения. 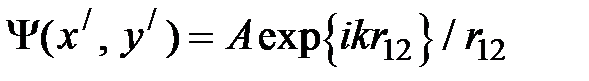 – амплитуда источников.
– амплитуда источников. 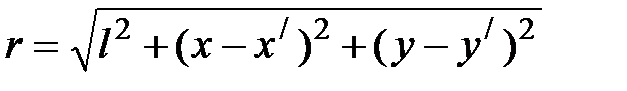 .
.
При малых углах обычно соблюдаются и следующие неравенства:
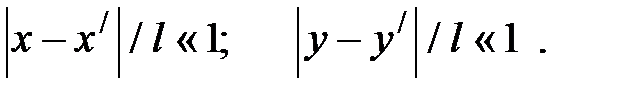
Тогда с учетом этого разложим r в ряд и ограничимся квадратичными членами.
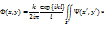
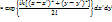
где медленно изменяющаяся величина r» l в знаменателе вынесена за интеграл, т.к. она на влияет на видность интерференционной картины, а только слабо влияет на общую яркость. Полученное приближение называется приближением Френеля, а соответствующая ему дифракция – дифракцией Френеля.
Дифракция Фраунгофера.
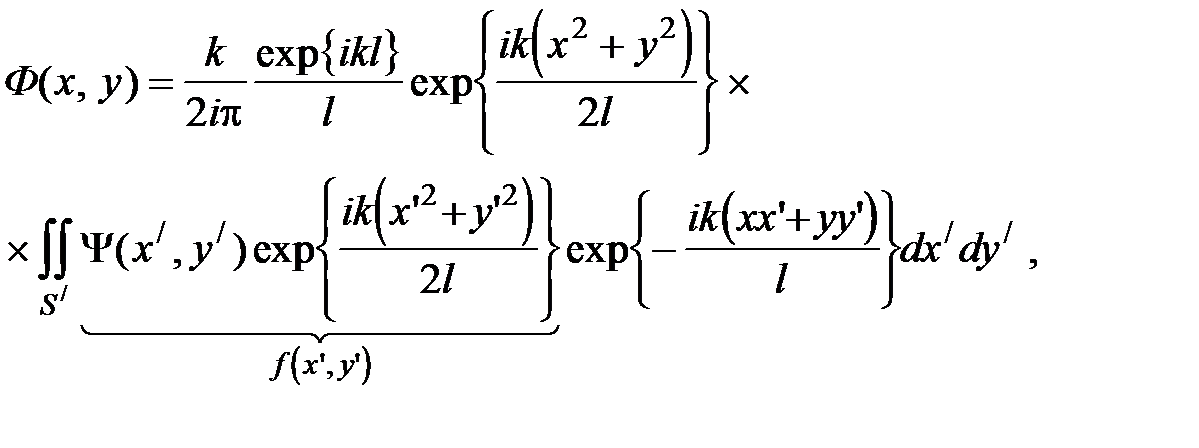 Если рассматривать в дальнейшем относительное распределение интенсивности, а не поля в дифракционной картине, то наличие комплексных экспонент перед интегралом можно не учитывать. С другой стороны, если учесть, что
Если рассматривать в дальнейшем относительное распределение интенсивности, а не поля в дифракционной картине, то наличие комплексных экспонент перед интегралом можно не учитывать. С другой стороны, если учесть, что 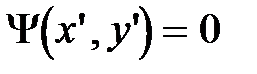 на непрозрачных частях экрана, то интегрировать можно по координатам от –¥ до +¥. Поэтому с точностью до множителей функция Ф(x,y) является Фурье–образом функции f(x’,y’) и для изучения дифракционных эффектов можно воспользоваться формализмом преобразований Фурье. Область дифракции Фраунгофера простирается от бесконечности до некоторого минимального значения:
на непрозрачных частях экрана, то интегрировать можно по координатам от –¥ до +¥. Поэтому с точностью до множителей функция Ф(x,y) является Фурье–образом функции f(x’,y’) и для изучения дифракционных эффектов можно воспользоваться формализмом преобразований Фурье. Область дифракции Фраунгофера простирается от бесконечности до некоторого минимального значения:
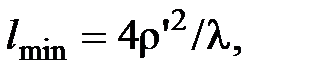 где r’ – максимальное расстояние от центра до края отверстия, на котором происходит дифракция. В области дифракции Фраунгофера:
где r’ – максимальное расстояние от центра до края отверстия, на котором происходит дифракция. В области дифракции Фраунгофера:
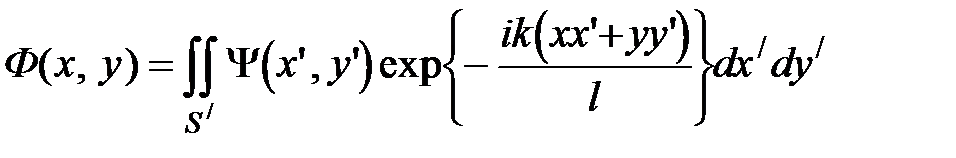
Date: 2015-05-17; view: 1404; Нарушение авторских прав