Приклади побудови перспективи відрізка прямої лінії

Приклад 1. Пряма загального положення (висхідна) довільно розташована відносно предметної і картинної площин.

Розв’язання. Для побудови перспективи прямої досить побудувати перспективи точок, розташованих на цій прямій, наприклад, точки початку прямої і нескінченно віддаленої точки. Точка початку прямої буде точкою зустрічі прямої з картиною.

На рис.3.2 дані висхідна пряма АВ, точка зору S, картина К і предметна площина p_1.

Приступаючи до побудови перспективи А°В° прямої АВ, необхідно продовжити пряму до перетину з картиною в точці N. Перспектива Nº початку прямої N збігається з самою точкою. Потім будується перспектива Е_пº безконечно віддаленої точки Е∞ прямої АВ. Точка Е_пº – точка сходу перспективи А°В° прямої АВ та прямих, паралельних їй. З’єднавши перспективи Nº і Е_пº (точки початку прямої безконечно віддаленої точки), одержують перспективу напрямку прямої. Слід підкреслити, що точка сходу Е_пº перспективи будь-якої прямої визначається точкою перетину проекціюючого променя, що йде з точки S паралельно даній прямій, з картиною.

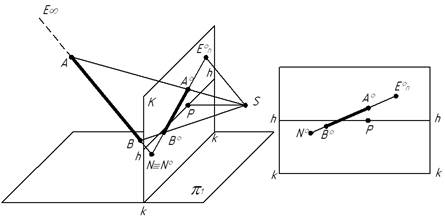
Рисунок 3.2 – Побудова перспективи прямої

Перспективи паралельних прямих завжди будуть спрямовані із своїх початкових точок в точку сходу Е_пº, яка для всіх них буде спільною, тому що промінь зору, що визначає точку сходу, буде, очевидно, паралельний для всіх них. Точка сходу висхідних прямих буде лежати вище горизонту, вона називається небесною точкою сходу і позначається Е_пº. Точка сходу низхідних прямих Е_оº буде розташована нижче горизонту і називається земною точкою сходу.

Приклад 2. Низхідна пряма загального положення.

Розв’язання. Для отримання перспективи відрізка прямої АВ достатньо побудувати перспективу двох її точок і з’єднати їх прямою лінією. Пряма лінія загального положення може бути задана в перспективі за допомогою її характерних точок: Fº – нескінченно віддаленої точки прямої і Nº – точки початку прямої (рис.3.3). Ці точки визначають пряму та її перспективу, якими користуються при побудові перспективи різних предметів.

Рисунок 3.3 – Побудова перспективи прямої загального положення

На рис. 3.3 в предметному просторі задано відрізок АВ і його горизонтальна проекція А'В' на предметній площині. Пряму АВ і її основу А'В' продовжують до перетину з картиною в точках N₁º і Nº. Кожна з цих точок є початком перспективи заданої прямої. Вторинна проекція N₁º початку прямої розташована на основі картини. Щоб знайти точку початку прямої, із точки N₁º опустити перпендикуляр до основи картини, який, перетинаючись з прямою АВ, визначить початок прямої Nº.

Для побудови перспективи точки Fº необхідно з точки зору S провести промінь паралельно прямій АВ, а два променя з точки зору S і з основи точки зору S', паралельно горизонтальній проекції А'В'. Точки Fº і її вторинна проекція F₁º розташовується на спільній вертикальній прямій, яка проведена з точки F₀.

Вторинна проекція F₁º знаходиться на лінії горизонту.

Приклад 3. Горизонтальна пряма, паралельна площинам p₁ і К.

Розв’язання. На рис.3.4 в перспективній системі дана пряма А'В', паралельна p₁ і К. Через точки А' і В' проводять з точки S проекціюючий промінь або проекціюючу площину. Лінія перетину АºВº цієї площини з картиною буде перспективою шуканої прямої А'В'. Перспектива горизонтальних прямих, паралельних основі картини, розташовується завжди паралельно горизонту і не має з ним точки сходу.

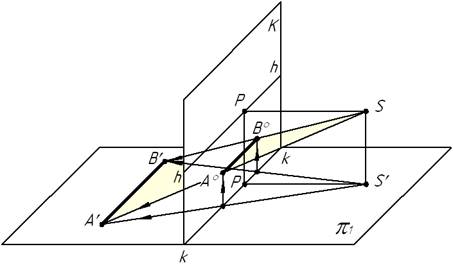
Рисунок 3.4 – Приклад побудови перспективи прямої

Приклад 4. Перспектива вертикальної прямої.

Розв’язання. На рис. 3.5 дана пряма АА'. Перспективу прямої можна розглядати як лінію перетину картини з проекціюючою площиною, що проходить через точку зору S і пряму АА'. Через те, що проекціююча площина, яка проходить через вертикальну пряму, перпендикулярна p₁, то й лінія перетину АºА₁º, що є перспективою вертикальної прямої АА' завжди буде перпендикулярна горизонту.

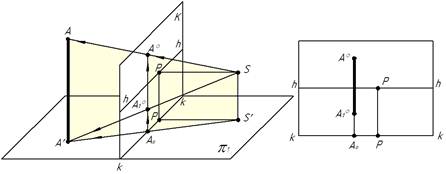
Рисунок 3.5 – Приклад побудови перспективи прямої

Date: 2015-04-23; view: 1480; Нарушение авторских прав