Дополнительные задачи. 232.параллелограмм, а точка .Е на стороне ВС такая, что \ВЕ\ : \ЕС\ = 2:3

232.параллелограмм, а точка.Е на стороне ВС такая, что \ВЕ\: \ЕС\ = 2:3. Выразите вектор АЕ через векторы АВ и ~АС ■

233.Докажите, что если диагонали четырехугольника при пересечении
делятся пополам, то такой четырехугольник есть параллелограмм.

234.Докажите, что отрезок, соединяющий середины диагоналей
трапеции, параллелен основаниям.

235.Дан параллелепипед ABCDA₁B₁C₁D₁. M,N,P — середины отрез­
ков DD_V CD_V BC₁ соответственно. Разложите по векторам

= АВ\, q = AD, г = Аа7 векторы: 1) АВ; 2) ~АС\; 3) AN;

236. Вне плоскости параллелограмма ABCD взята точка О, Разло­
жите по векторам а = ОА, Ь = ОВ, с=ОС векторы: 1) QM, где

М = (AC) n (BD); 2)OD;3)OK, где К— середина AD.

237.Найдите координаты вершины и координаты точки пересече­
ния диагоналей параллелограмма ABCD: 1) А(0; 0; 0), В(1; 2; 3),
С(-1; 1; -2); 2) А(-1; 2; 1), В(0; 4; 4), С(-2; 3; -1).

238.С помощью векторов докажите, что если прямая перпендикулярна
двум сторонам треугольника, то она перпендикулярна и третьей
стороне.

239.Три ребра тетраэдра, исходящие из одной вершины, равны, углы
между ними тоже равны. Докажите, что каждое ребро такого
тетраэдра перпендикулярно противоположному.

240.Точка К— середина ребра АС правильного
тетраэдра ABCD. Найдите косинус угла меж­
ду прямыми АВ и KD.

241.Скорость течения реки — 1,2 м/с. Катер
движется со скоростью 3 м/с перпендикулярно
берегу. Определите скорость движения катера
по отношению к реке.

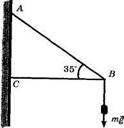
242.К концу кронштейна приложена сила
F = mg = 42 Н. Найдите силу сжатия стержня
ВС и силу растяжения стержня АВ (рис. 69).

243.закреплена в точках А и С, а в
точке В приложена сила F= mg— 45 Н. Най­
дите силу натяжения на участках АВ и ВС
(учитывая, что АВ расположена горизон­
тально, рис. 70).

244.Проволока закреплена в точках А и В, а в
точке С приложена сила F= mg = 45 Н.
Найдите силу натяжения на участках АС и
ВС, если точки А и В находятся на одном
уровне (рис. 71).

245.Основание АВ равнобедренного треугольни­
ка ABC лежит в плоскости а (а * (ABC)).
Какой угол больше: 1) угол между прямой
АС и а? 2) между прямой CD и а? (D —
середина стороны АВ).

246.Проекция равностороннего треугольника
на плоскости, проходящей через одну из его
сторон — прямоугольный треугольник. Най­
дите угол между стороной треугольника и
плоскостью проекции.

247.Дан ромб с диагоналями d_x и d₂. Через его

сторону проведена плоскость у, образующая с другой стороной угол. Найдите площадь проекции ромба на плоскость.

248.Концы отрезков АВ и CD принадлежат параллельным плоскос­
тям а и (3. Проекции этих отрезков на одну из плоскостей
соответственно равны а и Ъ, а углы ((АВ) Z. ос) и ((CD) Z. а) относят­
ся как 1:2. Найдите расстояние между плоскостями.

249.Из точек А иВ, принадлежащих одной из граней двугранного угла,
проведены перпендикуляры AA_V BB₁ на плоскость другой грани
и перпендикуляры АА₂, ВВ₂ на ребро. Найдите:

1) |ВВ₂|, если lAA^ =15 см, |BBJ = 27 см, |АА₂| = 20 см; 2) |АА_Х| и IBBJ, если \А_гА₂\ = т, \В_ГВ₂\ = п, \АА_Х\ + \ВВ₁\ =р.

250.Угол между плоскостями ABC и DBC равен 45°. Найдите \AD\,
если |АВ|=15 см,|ВС|=14 см, |АС|=13 см, \DB\=\DC\= 9 см.

251.Концы отрезка АВ принадлежат граням двугранного угла,
равного ф. Из точек А и В проведены перпендикуляры АС и BD к
ребру двугранного угла. Известно, что \АС\ = 10 см, \BD\ = 5 см,
\СЦ = 12 см. Найдите |АВ|, если: 1) ф = 90°; 2) ф = 60°.

252.Гипотенуза прямоугольного треугольника лежит в плоскости а,
его катеты наклонены к этой плоскости под углами 30° и 45°.
Найдите угол между плоскостью треугольника и плоскостью а.

253.В тетраэдре ABCD все ребра, кроме ребра ВС, имеют равные
длины, ZCAB = 90°. Найдите величину двугранного угла АВ.

Date: 2015-04-23; view: 1526; Нарушение авторских прав