
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Применение векторов
|
|
Векторы широко применяются в математике и физике. В геометрии с их помощью выводят уравнения плоскостей, прямых и других фигур, решают многие интересные задачи. Для этого данные в задаче соотношения между геометрическими и физическими объектами сначала как бы переводят на язык векторов. После чего преобразовывают полученные векторные равенства и снова переводят их на обычный язык геометрии или физики.
В школьной практике часто используют следующие равенства и утверждения:
1. Если прямые АВ и CD перпендикулярны, то АВ • CD = 0;
2. о*& = |а| * |б| -coscp;
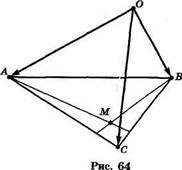
3. Если О — любая точка в пространстве, а М — середина отрез
ка АВ (рис. 63) или точка пересечения медиан треугольника ABC
(рис. 64), то соответственно
ОМ =±(рА + Ов) или ОМ=з (оА + ОВ + Об). Докажем последние равенства. Для любых трех точек справедливы равенства ОМ +М~А = ОА, ОМ+МВ = ОВ, ОМ+~МС = ОС.
Если сложим два первых из них и учтем, что MA + MB = 0, получим 2 • ОМ =ОА + ОВ, откуда ОМ=12{рА + О~в).
Если теперь сложим все три равенства и учтем, что MA + MB + + МС = б, получим, 3 • ОМ =ОА + ОВ + ОС, откуда
(рис. 64).
 Приведем несколько примеров на применение векторов в математике и физике.
Приведем несколько примеров на применение векторов в математике и физике.
 м
м
Рис. 63
1. Составить уравнение плоскости, перпендикулярной вектору ft (a; b; с), и проходящей через точку М(х0, у0, z0).
Решение. Пусть К(х, у, г) — произвольная точка рассматриваемой плоскости а
Векторы п (а; Ъ; с) и МК (х - х0; у - у0; г- г0) перпендикулярны. Поэтому их скалярное произведение равно ну () + Ъ • (у - у0) + с • (г - z0) = 0.
Это и есть искомое уравнение плоскости а. Если обозначить d = -(а • х0 + Ъ • у0 + с zo+ d), его можно представить в виде
и + cz + d = 0.
Итак, координаты х, у, г каждой точки плоскости а удовлетворяют полученному уравнению. Можно доказать также, что координаты любой точки, не лежащей на плоскости а, этому уравнению не удовлетворяют.
Пример 2. Требуется доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон.
| в |

|
Доказательство. Пусть ABCD параллелограмм (рис. 66).
Ясно, что A^C = a + b, DB = a-b. Обе части этих равенств скалярно ум-
себя: АС ={а +
| Рис. 66 |
ножим сами на
и
Найдем сумму квадратов диагоналей:
Теперь с учетом равенств a = АВ = DC
и b = AD = ВС, получим:
АС2 + DB2 = АВ2 + ВС2 + DC2 + DA2.
Что и требовалось доказать.
Пример 3. ABCDAiB1ClD1~ прямоугольный параллелепипед, К— точка пересечения медиан треугольника AJ5D. Доказать, что прямая АСХ проходит через.К" и определить, в каком отношении точка К делит отрезок АСг (рис. 67).
 Решение. Так как К— точка пересечения медиан треугольника AtBD, то АК = 1 (аа[ + АВ + IB}.
Решение. Так как К— точка пересечения медиан треугольника AtBD, то АК = 1 (аа[ + АВ + IB}.
Так как AB = DiC1 и AD = A1D1, то
 Значит АйГ= ACj. Из последнего равенства следует, что точка К лежит на прямой ACV с другой стороны, |ACX| = 3 • |АК], следовательно, |АК|: \KCj\ = 1:2. Задача решена.
Значит АйГ= ACj. Из последнего равенства следует, что точка К лежит на прямой ACV с другой стороны, |ACX| = 3 • |АК], следовательно, |АК|: \KCj\ = 1:2. Задача решена.
|
| F, |
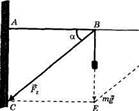
Пример 4. К концу кронштейна приложена сила F=mg=20H. ос = 40°. Найдите силу растяжения стержня АВ и силу сжатия стержня ВС (рис. 68).
| Рис 68 |
Решение. Рассмотрим парал- лелограмм BDEC. Силы, действующие на стержни, направлены по сторонам параллелограмма BD и ВС. Считая, что в треугольнике ВСЕ известны
катет \ВЕ\ = 20 и угол ZCBE = 50°, найдем катет СЕ и гипотенузу ВС.
Имеем:
\BD\ = \СЕ\ = | F, | = 20 • tg50°«23,8 (Н),
 Пример 5. (На использование скалярного произведения в физике). Сила в 16 Н, действующая в направлении движения под углом 45°, передвинула тело на расстояние 4 м. Определите работу, совершенную при помощи этой силы.
Пример 5. (На использование скалярного произведения в физике). Сила в 16 Н, действующая в направлении движения под углом 45°, передвинула тело на расстояние 4 м. Определите работу, совершенную при помощи этой силы.
Решение. Действующую силу выразим через F, а направление движения тела через s.
Тогда \р\ = 16, |3| = 4м, ф = (>3) = 45°.
Если для определения работы воспользуемся формулой А = | р I х х | s | • cos ф, получим А = 16 • 4 • cos45°«49 (Дж).
Если направление действия силы будет равнонаправлено с направлением движения, то ф = 0, a cos ф = 1. Формула вычисления работы будет А = F
. Задачи
А
220.Векторы а, b, a + b построены с одной и той же точки. Если
вектор а + b делит угол между векторами а и & на равные части,
то какими будут векторы а и b?
221.Угол между векторами АВ и CD равен 60°. Найдите угол между
векторами: 1) ВА и CD; 2) AS и DC.
222. ABC — правильный треугольник, а О —точка пересечения высот.
Докажите, что ОА + ОВ+ОС = б.
223.С помощью векторов докажите, что диагонали ромба взаимно
перпендикулярны.
224.Катер прошел в направлении к северо-западу 2 км, а потом,
повернув на север, еще 1 км. Выберите масштаб, постройте вектор
перемещения и найдите его длину.
В
225. ABCD — тетраэдр, у которого основанием является треугольник
ABC. Все ребра тетраэдра равны. Точка Е —середина отрезка DA,
а точка F —середина стороны ВС. Докажите, что EF -AD = 0.
226.С помощью векторного метода докажите, что диагонали
прямоугольника равны.
227.С помощью векторов докажите, что высота прямоугольного
треугольника, опущенная на гипотенузу, есть среднее пропор
циональное между двумя отрезками, на которые он делит гипо
тенузу.
228.Докажите, что средняя линия треугольника параллельна его
основанию и равна половине основания.
229.Докажите, что средняя линия трапеции равна половине суммы
ее оснований.
230.Катер движется со скоростью 5 м/с перпендикулярно к берегу.
Ширина реки 720 м, скорость течения 1 м/с, вследствие чего за
каждые 5 м пройденного пути катер относит в сторону пер
пендикулярно курсу на 1 м. На сколько метров он уйдет в сторону,
пока достигнет противоположного берега?
231.У пирамиды ABCD ребра AD и ВС, BD и АС перпендикулярны.
Докажите, что ребра CD и АВ также перпендикулярны.
Date: 2015-04-23; view: 4070; Нарушение авторских прав