Скалярное произведение векторов

Определение. Скалярным произведением векторов а (а_х; а₂; а₃) и Ъ Фу) Ь₂; Ь₃) называется число а₁ • Ь_х + о₂ • Ь₂ + а₃ • Ь₃.

Таким образом, по определению а • Ъ = а_г • Ь_х + а₂ • Ъ₂ + а₃ • b_r Так же, как и на плоскости, в пространстве доказываются четыре свойства

скалярного произведения:

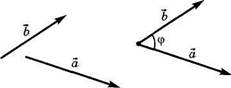
Определение. Углом

между двумя векторами называется величина образуемого ими угла, когда ониисходят от одной точки (рис. 62).

Угол между противоположно направленными векторами равен 180°, а между сонаправленными — 0°.

Теорема 21. Скалярное произведение векторов равно произведе­нию их абсолютных величин на косинус угла между ними, т. е. COS ф.

Теорема доказывается так же, как и на плоскости.

Из последнего равенства для ненулевых векторов следует:

Задача 3. Найдите косинус угла между векторами а (1; -2; 2) Решение, а • Ъ • совф = а• Ъ. Отсюда

Вопросы и задания

1. Какие векторы называются компланарными?

2. Какие векторы называются не компланарными?

3. Какие векторы называются ортами?

4. Как вычислить скалярное произведение двух векторов?

5. Повторите и запомните свойства скалярного произведения.

6. Запомните теорему о скалярном произведении векторов.

7. Объясните, почему скалярное произведение перпендикулярных векторов равно
нулю?

Задачи

А

210.В треугольнике ABC угол С прямой, а /. В = 40°. Найдите угол
между векторами: 1) СА и СВ; 2)ВАи СА; 3) СВ и ВА.

211.Найдите скалярное произведение векторов: 1) 3(1; 2; 4),

Ь(-8; 2; 1); 2) р{-2; -3; 1) и q(2; 3; 1).

212. При каком значении п данные векторы перпендикулярны:

1) а (2; -1; 3), Ъ (1; 3; п); 2) а (га; -2; 1), Ъ (п; -га; 1)?

213.Найдите угол между векторами т(-2; 2; 1) и га (-1; 0; 1).

214.Даны четыре точки А(0; 1; -1), В(1; -1; 2), С(3; 1; 0), D(2; -3; 1).

Найдите косинус угла между векторами АВ и CD.

В

215.Даны векторы а (1; -5; 2) и Ь (3; 1; 2). Найдите скалярное произ­
ведение векторов 2а + b и За - 2Ь.

216.Даны точки А(0; 1; -1), В(1; -1; 2), С(3; 1; 0). Найдите косинус
угла С треугольника ABC.

217.В тетраэдре DABC точка Е — середина стороны ВС, а точка О —

середина стороны АЕ. Выразите DO через векторы DA

С

218. Из вершины прямого угла А треугольника ABC восстановлен
перпендикуляр AD к плоскости треугольника. Найдите косинус

угла ф между векторами ВС и BD, если угол ABD равен a, a угол ABC равен |3.

219. Наклонная образует с плоскостью угол 45°. Через основание
наклонной проведена прямая в плоскости под углом 45° к
проекции наклонной. Найдите угол ф между этой прямой и
наклонной.

Date: 2015-04-23; view: 1763; Нарушение авторских прав