
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Термодинамические процессы идеальных газов в закрытых системах
|
|
Кратко рассмотрим основные термодинамические процессы идеального газа, закономерности которых понадобятся в дальнейшем, в частности, при рассмотрении циклов двигателей.
Изохорный процесс. При изохорном процессе выполняется условие dv = 0 или v = const. Из уравнения состояния идеального газа следует, что 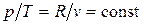 , т.е. давление газа прямо пропорционально его абсолютной температуре:
, т.е. давление газа прямо пропорционально его абсолютной температуре:
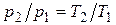 . (4.1)
. (4.1)
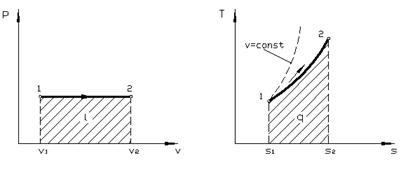
На рис. 4.1. представлен график процесса.
| Рис. 4.1. Изображение изохорного процесса в p, v – (а) и T, s – (б) координатах |
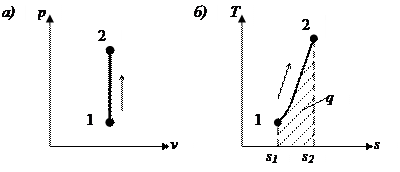
Работа расширения в этом процессе равна нулю, так как dv = 0.
Количество теплоты, подведенной к рабочему телу в процессе 12
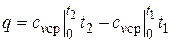 .
.
Так как l = 0, то в соответствии с первым законом термодинамики 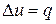 и
и
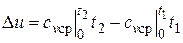 . (4.2)
. (4.2)
Поскольку внутренняя энергия идеального газа является функцией только его температуры, то формула (4.2) справедлива для любого термодинамического процесса идеального газа.
Изменение энтропии в изохорном процессе определяется из формулы (3.4) при v 1 = v 2, поскольку 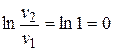 :
:
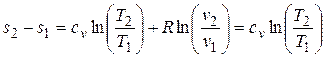 , откуда
, откуда 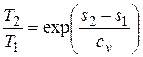 , (4.3)
, (4.3)
т.е. зависимость Т от s (в T-s диаграмме) является экспоненциальной (см. рис. 4.1).
Изобарный процесс. Из уравнения состояния идеального газа при р = const находим 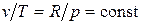 , или
, или
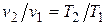 , (4.4)
, (4.4)
т.е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1820 г.). На рис. 4.2 изображены графики процесса в p, v- и T, s- диаграммах.
| Рис. 4.2. Изображение изобарного процесса в p, v - и T, s - координатах |
Из выражения (2.6) следует, что
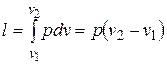 . (4.5)
. (4.5)
Так как 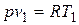 и
и 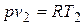 , то одновременно
, то одновременно
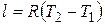 . (4.6)
. (4.6)
Количество теплоты, сообщаемой газу при нагревании (или отдаваемой им при охлаждении), находим из уравнения (2.24)
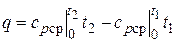 . (4.7)
. (4.7)
Из уравнения (2.28) 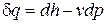 при р = const получим
при р = const получим
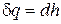 или
или 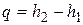 ,
,
т.е. количество теплоты, подведенной в изобарном процессе к закрытой системе, равно разности ее энтальпий. Сравнивая выражение первого закона термодинамики, определенное через энтальпию для изобарного процесса, с формулой (4.7), получим выражение для подсчета энтальпии
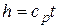 .
.
Формулу для изменения энтропии в изобарном процессе получим, подставив в уравнение 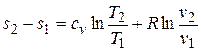 отношение
отношение 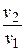 вместо
вместо 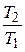 (из уравнения (4.4)) и с р вместо cv + R из уравнения (2.20):
(из уравнения (4.4)) и с р вместо cv + R из уравнения (2.20):
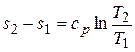 или
или 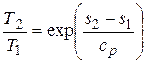 . (4.8)
. (4.8)
В T,s - диаграмме изобара тоже является экспонентой, как и изохора, но поскольку cp > cv, она положе.
Изотермический процесс. При изотермическом процессе температура постоянна, следовательно, 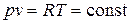 , или
, или
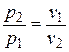 , (4.9)
, (4.9)
т.е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – падает (закон Бойля – Мариотта, 1662 г.).
Графиком изотермического процесса в p, v - координатах, как показывает уравнение (4.9) является равнобокая гипербола, для которой координатные оси служат асимптотами (рис. 4.3).
Поскольку температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (D u = 0) и вся подводимая к газу теплота полностью превращается в работу расширения:
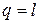 . (4.10)
. (4.10)
| Рис. 4.3. Изображение изотермического процесса в p, v - и T, s - координатах |
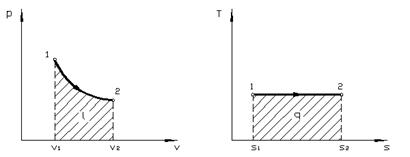
При изотермическом сжатии от газа отводится теплота в количестве, равном затраченной на сжатие работе.
Адиабатный процесс. Процесс, происходящий без теплообмена с окружающей средой (d q = 0), называется адиабатным. Для того чтобы осуществить такой процесс, следует либо теплоизолировать газ, т.е. поместить его в адиабатную оболочку, либо провести процесс настолько быстро, чтобы изменение температуры газа, обусловленное его теплообменом с окружающей средой, было пренебрежимо мало по сравнению с изменением температуры, вызванным расширением или сжатием газа.
Уравнение первого закона термодинамики для адиабатного процесса в закрытой системе можно записать в виде
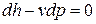 и
и 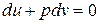 . (4.11)
. (4.11)
Имея в виду, что 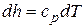 , а
, а 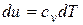 , и поделив с учетом этого первое из уравнений (4.11) на второе, получим,
, и поделив с учетом этого первое из уравнений (4.11) на второе, получим,
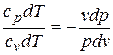 или
или 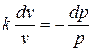 .
.
Интегрируя последнее уравнение при условии, что 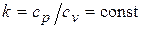 , находим
, находим
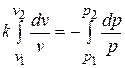 и
и 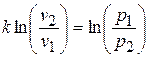 .
.
После потенцирования имеем 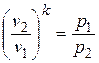 , или
, или
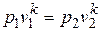 . (4.12)
. (4.12)
Это и есть уравнение адиабаты идеального газа при постоянном отношении теплоемкостей (k = const).
Величина
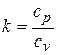 (4.13)
(4.13)
называется показателем адиабаты. Для одноатомного газа k = 1,66, для двухатомного k = 1,4, для трех- и многоатомных газов k = 1,33.
Поскольку k > 1, то в координатах p, v (рис. 4.4) линия адиабаты идет круче линии изотермы: при адиабатном расширении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.
| Рис. 4.4. Изображение адиабатного процесса в p, v - и T, s - координатах |
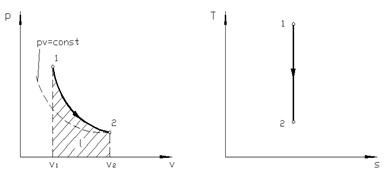
Записав из уравнения Клапейрона, написанного для состояний 1 и 2, отношение температуры через отношение давлений и заменив в нем отношение давлений через отношение объемов из уравнения (4.12) или наоборот, получим уравнение адиабатного процесса в форме, выражающей зависимость температуры от объема или давления:
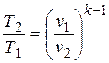 ;
; 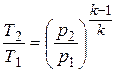 . (4.14)
. (4.14)
Работа расширения в адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии и может быть вычислена по формуле
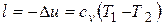 .
.
Из 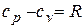 имеем
имеем 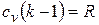 . Подставив отсюда cv в предыдущее соотношение, получим
. Подставив отсюда cv в предыдущее соотношение, получим
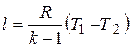 . (4.15)
. (4.15)
В данном процессе теплообмен газа с окружающей средой исключается, поэтому q = 0. Выражение 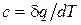 показывает, что теплоемкость адиабатного процесса равна нулю.
показывает, что теплоемкость адиабатного процесса равна нулю.
Поскольку при адиабатном процессе d q = 0, энтропия рабочего тела не изменяется (ds = 0 и s = const). Следовательно, на Т, s - диаграмме равновесный адиабатный процесс изображается вертикальной прямой линией.
Политропный процесс и его обобщающее значение. Любой произвольный процесс можно описать в p, v - координатах (по крайней мере, на небольшом участке) уравнением
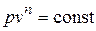 , (4.16)
, (4.16)
подбирая соответствующее значение n. Процесс, описываемый уравнением (4.16), называется политропным. Показатель политропы n может принимать любое численное значение в пределах от -¥ до +¥, но для данного процесса он является величиной постоянной.
Связь между параметрами в политропном процессе выражается теми же формулами, что и в адиабатном процессе с заменой показателя адиабаты k на показатель политропы n. Работа в политропном процессе 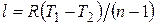 .
.
Date: 2015-05-09; view: 1765; Нарушение авторских прав