Изменение энтропии в неравновесных процессах

Выше говорилось, что в классической термодинамике рассматриваются только равновесные процессы. Реальные процессы в различной степени отличаются от равновесных: иногда незначительно (тогда можно без поправок применять все законы классической термодинамики), иногда – существенно. В последнем случае неравновесность приходится учитывать в расчётах. Этим занимается «неравновесная термодинамика», основателем которой является И. Пригожин.

Уже Р. Клазиус, а затем и И. Пригожин установили, что энтропия является специфической функцией. Она выступает в двух ипостасях. При рассмотрении равновесных систем она качественно не отличается от других известных нам функций состояния – u и h и используется в расчетах наряду с ними. Но она выступает в другом качестве при изучении неравновесных процессов, поскольку только она дает возможность характеризовать степень неравновесности процесса.

Возьмем термодинамическую систему (рабочее тело) в равновесном состоянии 1. Это значит, что его параметры (T ₁, v ₁, h ₁, s ₁ и т.д.) во всех точках одинаковы. Пусть эта система, совершив какой-то термодинамический процесс, перейдет в состояние 2. Мы не знаем, равновесным был этот процесс или нет, но мы можем выждать достаточно времени, чтобы состояние 2 стало равновесным (т. е. T ₂, s ₂ и т.д. стали одинаковыми по всему объему тела). В результате мы можем посчитать изменение любого параметра в этом процессе, в том числе и .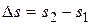

Рассмотрим принципиальные отличия неравновесных процессов от равновесных на примере расширения газа в цилиндре под поршнем (рис. 3.2), получающего теплоту d q от источника с температурой Т ₁ и совершающего работу против внешней силы Р, действующей на поршень.

Расширение будет равновесным только в случае, если температура газа Т равна температуре источника (Т = Т ₁), внешняя сила Р равна давлению газа на поршень (Р = pF), а при расширении газа нет ни внешнего, ни внутреннего трения. Работа расширения газа в этом случае равна 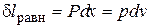, а изменение энтропии рабочего тела в таком процессе .

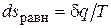Невыполнение хотя бы одного из указанных условий делает расширение газа неравновесным. Если неравновесность вызвана трением поршня о стенки цилиндра, то работа d l, совершаемая против внешней силы Р, оказывается меньше, чем pdv, так как часть ее затрачивается на преодоление трения и переходит в теплоту d q _тр. Она воспринимается газом вместе с подведенной теплотой d q, в результате чего возрастание энтропии газа в неравновесном процессе 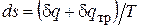оказывается больше, чем в равновесном при том же количестве подведенной от источника теплоты d q.

Если неравновесность вызвана отсутствием механического равновесия (P < pF), поршень будет двигаться ускоренно. Быстрое движение поршня вызывает появление вихрей в газе, затухающих под действием внутреннего трения, в результате чего часть работы расширения опять превращается в теплоту d q _тр. Работа против внешней силы снова получается меньше, а возрастание энтропии – больше, чем в равновесном процессе с тем же количеством теплоты d q.

Если неравновесность вызвана теплообменом при конечной разности температур (температура газа Т меньше температуры источника Т ₁), то возрастание энтропии рабочего тела оказывается больше, чем 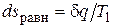в равновесном процессе из-за снижения температуры газа.

Итак, неравновесность всегда приводит к увеличению энтропии рабочего тела при том же количестве подведенной теплоты. Это выражение является одной из формулировок второго закона термодинамики.

Итак, для равновесных процессов справедливо соотношение . Разобранный пример достаточно наглядно показывает, что в неравновесных процессах 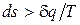, если d q – количество подведенной к системе или отведенной от нее теплоты, а Т – температура источника теплоты.

В общем виде это можно записать следующим образом

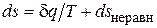, (3.7)

причем ds _неравн всегда положительно.

Соотношение (3.7) представляет собой математическую запись второго закона термодинамики.

Для адиабатно изолированных систем, которые по определению не обмениваются теплотой с окружающей средой (d q = 0), выражение (3.7) принимает вид

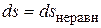. (3.8)

Если в адиабатно изолированной системе осуществляются равновесные процессы, то энтропия системы остается постоянной.

Самопроизвольные (а значит, и неравновесные) процессы в изолированной системе всегда приводят к увеличению энтропии.

Следует подчеркнуть, что равенство (3.8) применимо только к адиабатно изолированным системам. Если от системы отводится теплота, то ее энтропия может убывать и при протекании в ней самопроизвольных (неравновесных) процессов, когда 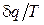в формуле (3.7) больше по абсолютной величине, чем ds _неравн.

Date: 2015-05-09; view: 1835; Нарушение авторских прав