Истечение газов и паров

Рассмотрим процесс равновесного (без трения) адиабатного истечения газов через сопло из резервуара, в котором газ имеет параметры р ₁, v ₁, Т ₁. Скорость газа на входе в сопло обозначим через с ₁. Будем считать, что давление газа на выходе из сопла р ₂ равно давлению среды, в которую вытекает газ.

Расчет сопла сводится к определению скорости и расхода газа на выходе из него, нахождению площади поперечного сечения и правильному выбору его формы.

Скорость истечения в соответствии с уравнением (5.10)

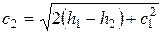. (5.11)

Выберем достаточно большую площадь входного сечения сопла, тогда с ₁ = 0 и

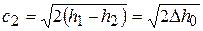, (5.12)

где D h ₀= h ₁ - h ₂ – располагаемый адиабатный теплоперепад.

Массовый расход газа m через сопло, кг/с, определяется из соотношения

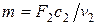, (5.13)

где F ₂ – площадь выходного сечения сопла.

Перепишем уравнение неразрывности стационарного потока (5.1) в сопловом аппарате в виде

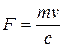, (5.14)

и возьмем дифференциалы от левой и правой частей уравнения (5.14) при условии m =const,

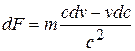. (5.15)

Разделив (5.15) на (5.14), получим

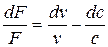, (5.16)

так как v и с – величины положительные, то изменение dF площади сечения вдоль сопла (по координате х) определяется отношением интенсивностей возрастания удельного объема газа 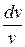и его скорости 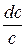в процессе его расширения.

Если скорость 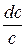увеличивается быстрее, чем удельный объем 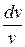, то сопло должно суживаться 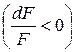, если же 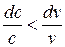– расширяться .

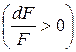В этом, кстати, и состоит отличие от случая истечения несжимаемой жидкости (воды), удельный объем которой не меняется по длине сопла (он не зависит от давления) и поэтому сопло для разгона жидкости всегда делают суживающимся.

При адиабатном равновесном расширении идеальных газов связь между давлением и объемом описывается уравнением (4.12): pv^k = const.

Опыт показывает, что с известным приближением это уравнение применимо и к адиабатному процессу водяного пара (для перегретого пара k = 1,3).

Преобразуем и продифференцируем уравнение адиабаты, обозначив const буквой С, получаем

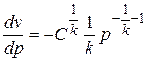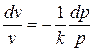, , . (5.17)

Разделив обе части уравнения (5.9) 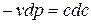на pv и умножив числитель и знаменатель правой части на с, найдем

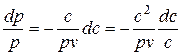. (5.18)

Подставив в (5.16) 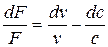вместо dv / v его выражение из (5.17), с учетом (5.18) получим

(5.19)

(из курса физики известно, что произведение kpv = kRT = a ², где а есть скорость звука в идеальном газе).

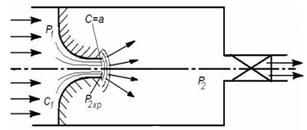
Для того чтобы наглядно представить смысл соотношения (5.19), поставим такой мысленный эксперимент. Пусть среда с параметрами р ₁, v ₁ через суживающееся сопло вытекает в объем с регулируемым давлением р ₂ (рис. 5.4).

Рис. 5.4. Схема истечения среды через суживающееся сопло в объем с регулируемым давлением при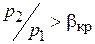

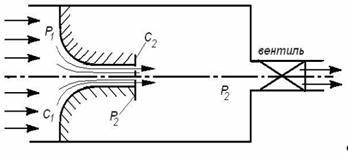
Давление р ₁ постоянно (например, это давление в заводской сети сжатого воздуха). Давление р ₂ будем регулировать вентилем. Когда вентиль полностью закрыт, среда через сопло не течет, т.е. m = 0 и р ₂ = р ₁. По мере открытия вентиля давление в сосуде будет уменьшаться, перепад давлений D р = р ₁ - р ₂ будет расти, в соответствии с ним будет увеличиваться и располагаемый теплоперепад D h ₀. Газ будет вытекать из сопла с большей скоростью с ₂ (см. формулу (5.12)).

Из курса физики известно, что возмущение давления распространяется со скоростью звука (собственно, звук и есть колебания давления). Приоткрывая вентиль, мы уменьшаем около него давление, и эта волна давления распространяется от вентиля к выходному срезу сопла, где установится такое же давление, как и у вентиля. При этом увеличится скорость истечения. Наконец, наступит такой момент, когда скорость истечения газа из сопла станет равной скорости звука в вытекающей среде. Импульс пониженного давления, распространяющийся со скоростью звука, не сможет проникнуть в сопло, т.е. внутри сопла изменения скорости потока не будет, как бы мы не открывали вентиль и не снижали давление р ₂. Отношение давления на срезе суживающегося сопла к давлению перед соплом, при котором скорость истечения становится равной скорости звука в вытекающей среде, называется критическим 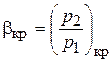. В качестве первого приближения можно принять 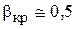. Более точно ее можно посчитать по специальным формулам.

Если р ₂ < р _2кр, то перепад давлений р _2кр – р ₂ срабатывается уже за пределами суживающегося сопла в виде ударных волн, или, как говорят, газодинамики, «скачков уплотнений». Никакого реультата, кроме дикого шума они не приносят (рис. 5.4, а).

а	б

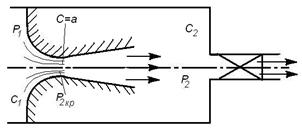
Рис 5.4. Схема истечения среды через суживающееся сопло (а) и сопло Лаваля (б) при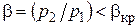

Способ использования энергии расширения газа до давления меньше критического и получения сверхзвуковой скорости вытекает из формулы 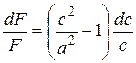(5.19): если с > а, то для увеличения скорости (dc > 0) нужно увеличивать площадь поперечного сечения сопла (dF > 0). Дело в том, что при c > a удельный объем газа настолько сильно увеличивается в процессе его расширения, что это требует увеличения площади поперечного сечения, несмотря на увеличение скорости. Впервые на это обратил внимание шведский инженер Лаваль в 80-х годах XIX века. Он предложил сужающееся сопло продолжить расширяющимся (рис. 5.4, б) чтобы дать возможность потоку плавно расширяться в нем от р _2кр до р ₂ без скачков уплотнений. Сейчас сопла Лаваля применяют в реактивных двигателях самолетов и ракет. Угол расширения не должен превышать 10 – 12°, чтобы не было отрывов потока от стен, приводящих к появлению скачков уплотнения.

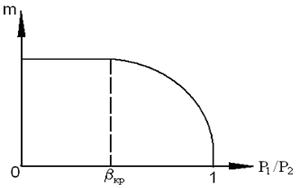
Расход газа от добавления расширяющейся части сопла не увеличивается (он по-прежнему будет определяться величиной скорости звука в самом узком «критическом» сечении – см. рис 5.5). А вот скорость истечения из такого сопла может существенно превышать скорость звука. Ее по-прежнему можно рассчитывать по формуле 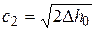, а площадь выходного сечения – по формуле 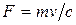(5.14).

Date: 2015-05-09; view: 1694; Нарушение авторских прав