
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теплоемкость газов
|
|
Упрощенно говоря, теплоемкостью С тела называют количество теплоты, которое нужно затратить в данном процессе, чтобы нагреть тело на один градус:  .
.
Обычно теплоемкость относят к единице количества вещества и в зависимости от выбранной единицы различают:
ü удельную массовую теплоемкость с, отнесенную к 1 кг газа, Дж/(кг×К);
ü удельную объемную теплоемкость с ´, отнесенную к количеству газа, содержащегося в 1 м3 объема при нормальных физических условиях, Дж/(м3×К);
ü удельную мольную теплоемкость μ с, отнесенную к одному киломолю, Дж/(кмоль×К).
Зависимость между удельными теплоемкостями устанавливается очевидными соотношениями:
с = μ с /μ; с ´= с ρн. (2.13)
Здесь ρн – плотность газа при нормальных условиях.
Изменение температуры тела при одном и том же количестве сообщаемой теплоты зависит от характера происходящего при этом процесса, поэтому теплоемкость является функцией процесса. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1 К различного количества теплоты. Численно величина с изменяется в пределах от + ∞ до – ∞.
В термодинамических расчетах большое значение имеют:
ü теплоемкость при постоянном давлении
с p = δ q p/ dT, (2.14)
равная отношению количества теплоты δ q p, подведенной к телу в процессе при постоянном давлении, к изменению температуры тела dT;
ü теплоемкость при постоянном объеме
сv = δ qv / dT, (2.15)
равная отношению количества теплоты δ qv, подведенной к телу в процессе при постоянном объеме, к изменению температуры тела dT.
В соответствии с первым законом термодинамики для закрытых систем δ q = du + pdv.
С учетом того, что 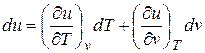 (соотношения (2.1))
(соотношения (2.1))
Δ q = (∂ u /∂ T) vdT + [(∂ u /∂ v) T + p ] dv. (2.16)
Для изохорного процесса (v =const) это уравнение принимает вид 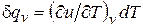 , и, учитывая (2.15), получаем, что
, и, учитывая (2.15), получаем, что
cv = (∂ u /∂ T) v. (2.17)
Для идеального газа 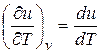 (уравнение 2.2), поэтому
(уравнение 2.2), поэтому
cv = du / dT. (2.18)
Для изобарного процесса (р =const) из уравнений (2.16) и (2.14) получаем
c p = (∂ u /∂ T) v + [(∂ u /∂ v) T + p ](dv / dT) p
Поскольку внутренняя энергия идеального газа определяется только его температурой и не зависит от удельного объема, то
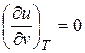 . (2.19)
. (2.19)
Из уравнения Клапейрона (1.4) pv = RT (1.3) следует 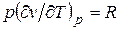 , откуда
, откуда
c p = сv + R. (2.20)
Соотношение (2.20) называется уравнением Майера и является одним из основных в технической термодинамике идеальных газов.
В процессе v =const теплота, сообщаемая газу, идет лишь на изменение его внутренней энергии, тогда как в процессе р = const теплота расходуется и на увеличение внутренней энергии и на совершение работы расширения. Поэтому c p больше с v на величину этой работы.
Формула  определяет так называемую истинную теплоемкость, т. е. значение теплоемкости при данной температуре. На практике теплоемкость широко используется для подсчета количества теплоты q 12, которое необходимо затратить, чтобы нагреть тело от одной температуры (t 1) до другой (t 2) (или которое выделится при охлаждении от t 2 до t 1).
определяет так называемую истинную теплоемкость, т. е. значение теплоемкости при данной температуре. На практике теплоемкость широко используется для подсчета количества теплоты q 12, которое необходимо затратить, чтобы нагреть тело от одной температуры (t 1) до другой (t 2) (или которое выделится при охлаждении от t 2 до t 1).
Если в указанном диапазоне температур теплоемкость не изменяется, то
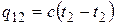 , кДж/кг и
, кДж/кг и  , кДж. (2.21)
, кДж. (2.21)
Эту формулу можно применять и для приблизительных (не очень точных) расчетов. Например, удельная теплоемкость воды при комнатной температуре равна 4,187 кДж/(кг×°С), а воздуха»1 кДж/(кг×°С). Поскольку теплоемкость почти всех веществ изменяется (чаще всего возрастает) с ростом температуры, нужно, строго говоря, использовать формулу
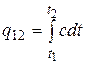 . (2.21 а)
. (2.21 а)
На рис. 2.2 величина q 12 изображена заштрихованной площадкой. Казалось бы проще всего, применив теорему о среднем, записать
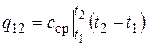 , (2.22)
, (2.22)
где 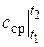 – среднее значение теплоемкости в диапазоне температур t 1… t 2.
– среднее значение теплоемкости в диапазоне температур t 1… t 2.
| Рис. 2.2. Зависимость истинной теплоемкости от температуры |
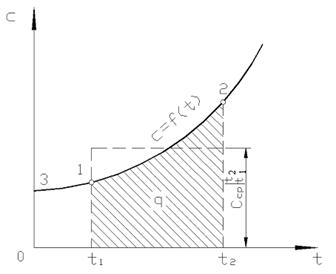
Однако для реальных расчетов такая запись очень неудобна, поскольку величину теплоемкости выбирают из таблиц, а 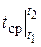 зависит как от t 1, так и от t 2. Таблица функции от двух аргументов получилось бы очень громоздкой.
зависит как от t 1, так и от t 2. Таблица функции от двух аргументов получилось бы очень громоздкой.
На практике поступают следующим образом. Искомое количество теплоты представляют в виде разности между ее количествами, необходимыми для нагрева тела от 0 °С до температур t 2 и t 1 соответственно (рис. 2.2)
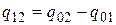 . (2.23)
. (2.23)
Тогда
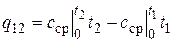 , (2.24)
, (2.24)
где 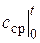 - средняя теплоемкость в диапазоне температур 0… t °С.
- средняя теплоемкость в диапазоне температур 0… t °С.
Величина средней теплоемкости 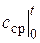 для данного вещества (и данного процесса, т.е. ср или cv) зависит лишь от одной температуры t. Именно эти теплоемкости и приводятся во всех таблицах под названием «средние». Сказанное справедливо как для с (ср и cv), так и для с ¢ и m с. В качестве примера в таблице, приведенной ниже, дана зависимость теплоемкости от температуры для некоторых наиболее распространенных газов. Нужно подчеркнуть, что в формуле (2.24) температура подставляется в градусах Цельсия.
для данного вещества (и данного процесса, т.е. ср или cv) зависит лишь от одной температуры t. Именно эти теплоемкости и приводятся во всех таблицах под названием «средние». Сказанное справедливо как для с (ср и cv), так и для с ¢ и m с. В качестве примера в таблице, приведенной ниже, дана зависимость теплоемкости от температуры для некоторых наиболее распространенных газов. Нужно подчеркнуть, что в формуле (2.24) температура подставляется в градусах Цельсия.
Средняя молярная теплоемкость различных газов при р =const
(по данным М.П. Вукаловича, В.А. Кириллина, В.Н. Тимофеева)
| t, °C | m ср, кДж/(кмоль×К) | |||||||
| О2 | N2 атмосферный | Н2 | СО | СО2 | SО2 | H2O | Воздух | |
| 29,278 | 29,022 | 28,621 | 29,127 | 35,865 | 38,859 | 33,503 | 29,077 | |
| 29,542 | 29,052 | 28,939 | 29,181 | 38,117 | 40,659 | 33,746 | 29,156 | |
| 29,935 | 29,135 | 29,077 | 29,307 | 40,065 | 42,334 | 34,123 | 29,303 | |
| 30,404 | 29,290 | 29,127 | 29,521 | 41,760 | 43,883 | 34,579 | 29,525 | |
| 30,882 | 29,504 | 29,109 | 29,793 | 43,255 | 45,223 | 35,094 | 29,793 | |
| 31,338 | 29,768 | 29,253 | 30,103 | 44,579 | 46,396 | 35,634 | 30,099 | |
| 31,765 | 30,048 | 29,320 | 30,429 | 45,759 | 47,359 | 36,200 | 30,408 | |
| 32,155 | 30,346 | 29,412 | 30,756 | 46,819 | 48,238 | 36,794 | 30,727 | |
| 32,506 | 30,639 | 29,521 | 31,074 | 47,769 | 48,950 | 37,397 | 31,032 | |
| 32,829 | 30,928 | 29,650 | 31,380 | 48,624 | 49,620 | 38,013 | 31,325 | |
| 33,122 | 31,200 | 29,793 | 31,669 | 49,398 | 50,165 | 38,624 | 31,602 | |
| 33,390 | 31,459 | 29,948 | 31,941 | 50,106 | 50,667 | 39,231 | 31,866 | |
| 33,637 | 31,711 | 30,111 | 32,196 | 50,747 | 51,086 | 39,830 | 32,113 | |
| 33,867 | 31,945 | 30,291 | 32,431 | 51,329 | --- | 40,412 | 32,347 | |
| 34,081 | 32,167 | 30,471 | 32,657 | 51,865 | --- | 40,482 | 32,569 | |
| 34,286 | 32,376 | 30,651 | 32,862 | 52,355 | --- | 41,530 | 32,778 | |
| 34,479 | 32,369 | 30,836 | 33,055 | 52,807 | --- | 42,062 | 32,971 | |
| 34,663 | 32,753 | 31,016 | 33,235 | 53,226 | --- | 42,581 | 33,155 | |
| 34,839 | 32,921 | 31,196 | 33,407 | 53,611 | --- | 43,075 | 33,323 | |
| 35,010 | 33,084 | 31,376 | 33,566 | 53,967 | --- | 43,544 | 33,486 | |
| 35,174 | 33,235 | 31,552 | 33,712 | 54,298 | --- | 44,001 | 33,645 | |
| 35,333 | 33,381 | 31,727 | 33,855 | 54,603 | --- | 44,399 | 33,792 | |
| 35,488 | 33,520 | 31,895 | 33,984 | 54,888 | --- | 44,856 | 33,930 | |
| 35,638 | 33,645 | 32,062 | 34,110 | 55,152 | --- | 45,261 | 34,064 | |
| 35,789 | 33,683 | 32,226 | 34,227 | 55,399 | --- | 45,651 | 31,190 | |
| 35,932 | 33,880 | 32,389 | 34,340 | 55,624 | --- | 46,023 | 34,311 |
В этой таблице величины m с р приведены через 100 °С. Поскольку они не сильно меняются с температурой, промежуточные величины можно находить путем линейной экстраполяции. Напомним, как это делается. Имеются табличные значения функции y = f (x) у 1 (при х = х 1) и у 2 (при х = х 2). Значение функции у (х) при х 1< х < х 2 равно 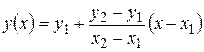 . Эта формула верна как для монотонно возрастающей функции (когда у 2> у 1), так и для монотонно убывающей (у 2< у 1); в этом случае дробь будет отрицательной, так как х 2 > х 1 всегда.
. Эта формула верна как для монотонно возрастающей функции (когда у 2> у 1), так и для монотонно убывающей (у 2< у 1); в этом случае дробь будет отрицательной, так как х 2 > х 1 всегда.
Date: 2015-05-09; view: 1314; Нарушение авторских прав